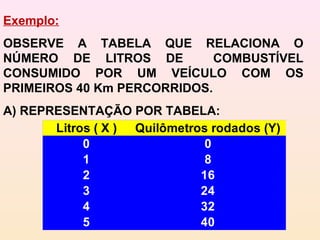
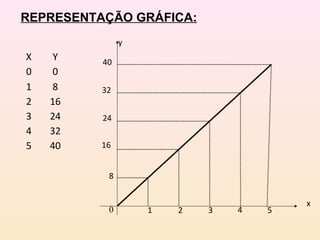
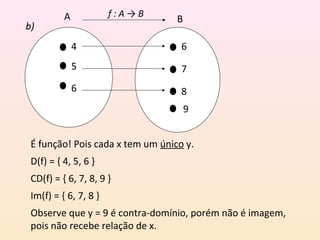
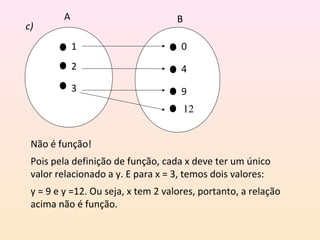
O documento aborda o conceito de função em matemática, explicando suas definições e representações por tabelas, diagramas e gráficos. Inclui exemplos práticos de funções, exercícios para identificar funções e cálculos de valores a partir de expressões funcionais. Além disso, destaca critérios para determinar se um gráfico representa uma função, proporcionando um guia didático sobre o tema.

1. FUNÇÕESFUNÇÕES
PROFESSOR: Me. JOÃO ALESSANDRO
CAMPO MOURÃO - PR
MAIO - 2017

2. FUNÇÕES

3. FUNÇÃO
FUNÇÃO É UM DOS CONCEITOS MAIS ÚTEIS EMFUNÇÃO É UM DOS CONCEITOS MAIS ÚTEIS EM
MATEMÁTICA E EM TODOS OS RAMOS DAMATEMÁTICA E EM TODOS OS RAMOS DA
TECNOLOGIA. TAIS COMO A FÍSICA, A MECÂNICA ETECNOLOGIA. TAIS COMO A FÍSICA, A MECÂNICA E
A ELETRICIDADE.A ELETRICIDADE.
DEFINIÇÃO
DADOS DOIS CONJUNTOS NÃO-VAZIOS, FUNÇÃO DE A
EM B É QUALQUER RELAÇÃO DE A EM B EM QUE
CADA ELEMENTO DE A ASSOCIA UM ÚNICO
ELEMENTO DE B.
REPRESENTAÇÃO
POR TABELAS, DIAGRAMAS E GRÁFICOS.

4. Exemplo:
OBSERVE A TABELA QUE RELACIONA O
NÚMERO DE LITROS DE COMBUSTÍVEL
CONSUMIDO POR UM VEÍCULO COM OS
PRIMEIROS 40 Km PERCORRIDOS.
A) REPRESENTAÇÃO POR TABELA:
Litros ( X ) Quilômetros rodados (Y)
0 0
1 8
2 16
3 24
4 32
5 40

5. ESSA RELAÇÃO CARACTERIZA UMA FUNÇÃO DEFINIDA
PELA EQUAÇÃO y = 8X
Litros ( X ) Quilômetros rodados (Y)
0 0
1 8
2 16
3 24
4 32
5 40
• O SEU DOMÍNIO É REPRESENTADO PELOS
VALORES DE X DA TABELA; D ( f ) = {0,1,2,3,4,5}
• O SEU CONJUNTO-IMAGEM REPRESENTADO PELOS
VALORES DE Y, OS QUAIS ESTÃO ASSOCIADOS A
CADA X DO DOMÍNIO: Im ( f ) = {0,8,16,24,32,40}

6. REPRESENTAÇÃO POR DIAGRAMAS:
X Y
0 0
1 8
2 16
3 24
4 32
5 40
1
2
3
4
5
8
16
24
32
40
A B
f : A → B
0 0

7. 10 2 3 4 5
x
8
16
24
32
40
y
REPRESENTAÇÃO GRÁFICA:
X Y
0 0
1 8
2 16
3 24
4 32
5 40

8. EXERCÍCIOS RÁPIDOS:
ANALISANDO CASOS DE FUNÇÕES
1. Diga quais diagramas abaixo que representam funções:
B
1
2
3
4
8
16
24
Aa)
Não é função,
pois x = 4 não
tem imagem!

9. É função! Pois cada x tem um único y.
D(f) = { 4, 5, 6 }
CD(f) = { 6, 7, 8, 9 }
Im(f) = { 6, 7, 8 }
Observe que y = 9 é contra-domínio, porém não é imagem,
pois não recebe relação de x.
B
4
5
6
9
6
7
8
A
b)
f : A → B

10. Não é função!
Pois pela definição de função, cada x deve ter um único
valor relacionado a y. E para x = 3, temos dois valores:
y = 9 e y =12. Ou seja, x tem 2 valores, portanto, a relação
acima não é função.
B
1
2
3
12
0
4
9
A
c)

11. RECONHECENDO SE UM GRÁFICO É
FUNÇÃO:
• Corta-se o gráfico com 2 retas paralelas ao
eixo y.
• Se as retas cortarem o gráfico em apenas 1
ponto, o gráfico é de uma função. Caso
contrário, não é função.

12. EXERCÍCIO
Assinale quais gráficos que representam funções:
É
função
Não é
função
É
função
Não é
função
x
y
x
y
x
y
x
y
a( )
b( ) d( )
c( )

13. CALCULANDO f(x)
Lembrete: f(x) = y
Exemplo: Sendo f(x) = 3x +1. Determine:
a) f(1) = ?
f(x) = 3x +1
f(1) = 3 . 1 + 1
f(1) = 3 + 1
f(1) = 4
b) f(-2) = ?
f(x) = 3x +1
f(-2) = 3 . (-2) + 1
f(-2) = - 6 + 1
f(-2) = -5

14. RESOLVENDO EXERCÍCIOS
1. Observe o gráfico da função abaixo:
y
x
-4 -2 1 2 3
3
5
6
3,5
Complete as questões seguintes:
a)f (-4) =
b)f (2) =
c)f (3) =
d)A função é crescente nos intervalos:
e)A função é decrescente nos intervalos:
f)A função é constante em:
5
6
3
[1;2]
[-4;-2] e [2; 3,5]
[-2, 1]

15. LEMBRETE
ESTA APRESENTAÇÃO ESTÁ NO
BLOG DO PROFESSOR
•SITE:
WWW.SLIDESHARE.NET/JOAOALESSANDRO