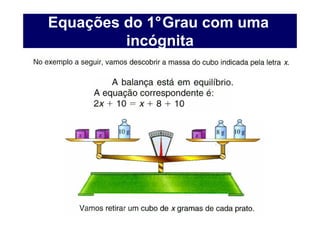
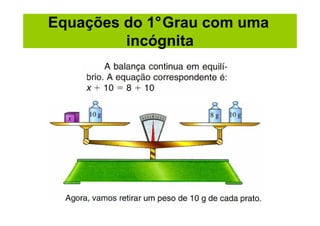
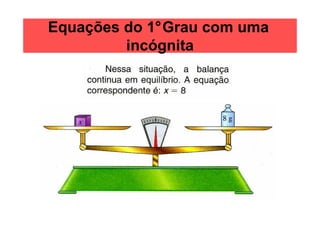
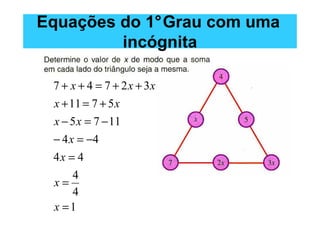
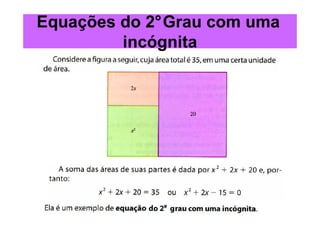
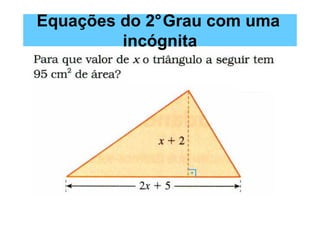
O documento discute equações de 1o e 2o grau com uma incógnita. Ele apresenta exemplos resolvidos de equações de 1o grau, como 2x - 1 = x + 5, e de 2o grau, como x2 - 3x - 180 = 0. O documento também introduz a fórmula geral para resolver equações de 2o grau.

1. Aula 12 – 09/06/2011
Prof. Paulo Berndt

2. Equações do
1°e 2 °graus

3. Equações do 1°Grau com uma
incógnita

4. Equações do 1°Grau com uma
incógnita

5. Equações do 1°Grau com uma
incógnita

6. Equações do 1°Grau com uma
incógnita

7. Resolução de Equações do 1°Grau
com uma incógnita
2x −1 = x + 5
2x − x = 5 +1
x=6
S = {6}

8. Equações do 1°Grau com uma
incógnita

9. Equações do 1°Grau com uma
incógnita
3 x + 250 = 2500
3 x = 2500 − 250
3 x = 2250
2250
x=
3
x = 750 g

10. Equações do 1°Grau com uma
incógnita
15 ⋅ 4 + x ⋅ 2 = 100
60 + 2 x = 100
2 x = 100 − 60
2 x = 40
40
x=
2
x = 20 motos

11. Equações do 1°Grau com uma
incógnita
1ª linha = 1ª coluna
16 + x + 4 + x + 9 = 16 + 11 + x + 7
2 x + 29 = x + 34
2 x − x = 34 − 29
x=5

12. Equações do 1°Grau com uma
incógnita
3 x + 50 = x + 42
3 x − x = 42 − 50
2 x = −8
−8
x=
2
x = −4

13. Equações do 1°Grau com uma
incógnita
x x
a) + x − 5 = + x − 10
3 2
2 x + 6 x − 30 3 x + 6 x − 60
=
6 6
2 x + 6 x − 30 = 3 x + 6 x − 60
8 x − 30 = 9 x − 60
8 x − 9 x = −60 + 30
− x = −30
x = 30

14. Equações do 1°Grau com uma
incógnita
b) AB = x − 5 = 30 − 5 = 25
x 30
BC = = = 15
2 2
x 30
CD = = = 10
3 3
DA = x − 10 = 30 − 10 = 20
Perímetro = 25 + 15 + 10 + 20
Perímetro = 70

15. Equações do 1°Grau com uma
incógnita
a) camisa → x x + 2 x + 2 x + 3,2 = 57,7
calça → 2 x 5 x = 57,7 − 3,2
5 x = 54,5
tênis → 2 x + 3,2 calça → 2 x
54,5
x= calça → 2 ⋅10,9
5
x = 10,9 calça → R$ 21,80

16. Equações do 1°Grau com uma
incógnita
tênis → 2 x + 3,2 = 2 ⋅10,9 + 3,2 = 21,8 + 3,2 = 25
duas camisas → 2 x = 2 ⋅10,9 = 21,8
R$ 25,00 + R$ 21,80 = R$ 46,80

17. Equações do 1°Grau com uma
incógnita
7 + x + 4 = 7 + 2 x + 3x
x + 11 = 7 + 5 x
x − 5 x = 7 − 11
− 4 x = −4
4x = 4
4
x=
4
x =1

18. Equações do 2°Grau com uma
incógnita

19. Equações do 2°Grau com uma
incógnita

20. Equações do 2°Grau com uma
incógnita
3 x ⋅ ( x + 5) = 0 Equação Incompleta do tipo c = 0.
3 x = 0 ou x + 5 = 0
x = 0 ou x = −5
S = {0,−5}

21. Equações do 2°Grau com uma
incógnita
Equação Incompleta do tipo b = 0.
9 3
x =
2
x=±
4 2
9  3 3
x=± S = + , − 
4  2 2

22. Equações do 2°Grau com uma
incógnita
− b ± b2 − 4 ⋅ a ⋅ c Equação Completa
x=
2⋅a
a = 1, b = −10, c = 24 10 + 2 12
x' = = =6
2 2
− (−10) ± (−10) 2 − 4 ⋅1 ⋅ 24
x= 10 − 2 8
2 ⋅1 x" = = =4
2 2
10 ± 100 − 96 10 ± 4 S = {4, 6}
x= =
2 2

23. Fórmula Resolutiva da Equação de
2°Grau

24. Equações do 2°Grau com uma
incógnita
(2 x) 2 = 2,5 ⋅ ( x + 2 x + x)
4 x 2 = 2,5 ⋅ 4 x
4 x 2 = 10 x
4 x 2 − 10 x = 0
2 x ⋅ (2 x − 5) = 0
2 x = 0 ou 2 x − 5 = 0
0
x= ou 2 x = 5
2
5
x = 0 ou x =
2

25. Equações do 2°Grau com uma
incógnita

26. Equações do 2°Grau com uma
incógnita
− 9 ± 9 2 − 4 ⋅ 2 ⋅ (− 180)
base × altura x=
A= 2⋅2
2
− 9 ± 81 + 1440
95 =
(2 x + 5) ⋅ (x + 2) x=
4
2 − 9 ± 1521
x=
190 = (2 x + 5) ⋅ ( x + 2 ) 4
− 9 ± 39
190 = 2 x + 4 x + 5 x + 10
2
x=
4
190 = 2 x 2 + 9 x + 10 − 9 + 39 30 15
x' = = =
2 x 2 + 9 x − 180 = 0 4 4 2
− 9 − 39 − 48
x' = = = −12
4 4

27. Equações do 2°Grau com uma
incógnita
− (− 3) ± (− 3) − 4 ⋅1 ⋅ (− 180)
2
x2
x=
− x = 60 2 ⋅1
3 3 ± 9 + 720 3 ± 729 3 ± 27
x= = =
x 2 − 3x 180 2 2 2
= 3 + 27 30
3 3 x' = = = 15 ⇒ 3 x = 45
2 2
x − 3x − 180 = 0
2
3 − 27 − 24
x' ' = = = −12 ⇒ 3 x = −36
2 2

28. Equações do 2°Grau com uma
incógnita

29. Equações do 2°Grau com uma
incógnita
x + x + x = 60 ⋅ 80
2 2 2
x
3x 2 = 4800
4800
x x x
x =
2
3
x 2 = 1600
x = ± 1600
x = ±40
O lado de cada terreno quadrado mede 40 metros.