Projeto Trigonometria Atualizado

TÓPICOS EM GEOMETRIA_1.2010 :: PROJETO DE APRENDIZAGEM Alunos: Izac Gonçalves dos Santos ; Luiz Paulo Scovino Lobo

Título: Aplicações e Problemas para demonstrar a importância das relações trigonométricas no dia a dia

1. Disciplina e anos envolvidos: Matemática, e ciências. 8ª e 9ª

2. Tema central : Aplicações e Problemas para demonstrar a importância das relações trigonométricas no dia a dia.

3. Temas de apoio: O presente projeto visa demonstrar também a utilização de um teodolito , objetivando que o estudante compreenda a importância que têm as relações trigonométricas ao desempenharem as medidas indiretas de distâncias e altura.

Metodologia Formação de um grupo com cinco estudantes; Realização de estudos e pesquisas sobre os triângulos (quanto aos lados, aos ângulos, semelhanças, relações métricas no triângulo retângulo, Teorema de Pitágoras); Promoção de debates entre os estudantes sobre as pesquisas; Confecção no Laboratório de Matemática de um instrumento tipo Teodolito ; Realização de apresentações (socialização) nas turmas dos trabalhos e da prática das razões trigonométricas; Avaliação individual e coletiva das apresentações.

4. Justificativa: Mostrar a importância da utilização da trigonometria no desenvolvimento da humanidade, e inserida nas atividades relacionadas as diferentes áreas profissionais, como: Engenharia, Física, Astronomia, Medicina, etc.

5. Objetivos gerais e específicos: O estudante: Certifica que existem parâmetros adequados para realização da medida de uma grandeza; Identifica diferentes métodos de medidas e aplicações adequadas; Utiliza a geometria para resolução de situações-problema; Distingue e identifica diferentes instrumentos de medidas; Opera quantitativamente os dados obtidos; Desenvolve competências e habilidades matemático-trigonométricas; Percebe que um trabalho motivado gera uma aprendizagem bem mais efetiva; Interliga teoria e prática para uma aquisição de aprendizagens mais significativa. Proporcionar aos alunos experiências cotidianas envolvendo trigonometria. Utilizar recursos tecnológicos e softwares de geometria dinâmica nas atividades propostas como o cálculo de distâncias inacessíveis.

6. Enfoque pedagógico : Sócio-construtivista.

7. Recursos tecnológicos: Utilização de ferramentas da Web 2.0 disponíveis na Internet Uso do programa de Geometria Dinâmica R.e.C. que é disponibilizado gratuitamente pela Internet . Instalação do Google Earth 5.0 (versão gratuita). DVD contendo arquivos com informações sobre a Floresta Amazônica. “ Data show” para apresentação de slides e vídeos da Amazônia. Computadores do laboratório de informática conectados a Internet para pesquisas e seleções de fotos, mapas e reportagens relacionadas aos tópicos em estudo e instalação do programa R.e.C. .

8. Etapas e suas estratégias de realização: Um pouco sobre a história da trigonometria. Aplicações e Problemas para demonstrar a importância das relações trigonométricas no dia a dia. Situações mais complicadas e interessantes, como a medição de distâncias inacessíveis (largura de um rio, altura de um morro, etc...), usando o teodolito para fornecer os ângulos necessários. Construção do teodolito. Associação entre os triângulos retângulos e as tabelas trigonométricas. A verificação, usando o software ReC da expressão do seno da soma. Pesquisa de profissionais, ou com profissionais, que utilizam a trigonometria em seu trabalho.

9. Definição de papéis: Papel do professor: facilitador no acesso às informações e na construção do conhecimento; mediador; integrador e ético (agir com responsabilidade). Papel do aluno: questionador; participativo; comprometido com os assuntos propostos; interagir com o grupo (colegas) trazendo suas experiências para serem discutidas; aprender a trabalhar em colaboração e de forma autônoma; comparar e relacionar “a trigonometria no nosso dia-a-dia ” com temas interdisciplinares.

10. Sites e bibliografia de apoio: IEZZI, Gelson. Fundamentos de matemática elementar 3: trigonometria . São Paulo: Atual Editora, 1993. DANTE, Luiz Roberto. Matemática – Contexto e Aplicações . Volume 2, 2º grau. Editora Ática, 2ª Edição. 2004, São Paulo. LOBO DA COSTA, Nielce M. A História da Trigonometria . Artigo – Pontifícia Universidade Católica, São Paulo. Disponível em < http://www.paulofreire.org/Biblioteca/histtrigon.pdf >. Acesso em: 31 de março de 2010. WIKIPÉDIA. Trigonometria – Conceitos e Definições . Disponível em < http://pt.wikipedia.org/wiki/Trigonometria >. Acesso em: 31 de março de 2010 WIKIPÉDIA. Definição e Demonstração da Lei dos Senos . Disponível em < http://pt.wikipedia.org/wiki/Lei_dos_senos >. Acesso em: 02 de. Acesso em: 31 de março de 2010 UM pouco da História da Trigonometria. Disponível em: < http://ecalculo.if.usp.br/historia/historia_trigonometria.htm >. Acesso em: 5 abr 2010. OLIVEIRA, Francisco Canindé de . História da matemática nas aulas de trigonometria. Disponível em: < http://www.sbem.com.br/files/ >. Acesso em: 5 abr 2010. IMENES, Luiz Márcio; LELLIS, Marcelo. Matemática para todos . São Paulo: Scipione, 2002. CHICA, Cristiane; JESUS, Humberto Luís de. Matemática. Brasília: Cisbrasil, 2008.

11. Coleta de dados: A coleta de dados será através de consultas em páginas da Internet , livros, revistas e jornais.

12. Seleção do material: Os materiais requeridos para a realização deste projeto são fundamentalmente originários de recursos da Web 2.0 , por se tratar de um meio de informação onde toda a sociedade pode ter acesso. Os alunos deverão ser orientados a escolherem fontes bibliográficas confiáveis, dando preferência aos sites oficiais e às ONGs que adquiriram credibilidade em virtude de ações em defesa da trigonometria.

13. Programação visual: Apresentação de slides e vídeos com imagens e notícias sobre as relações trigonométricas no nosso dia-a-dia. O uso do programa Google Earth 5.0 possibilita explorar conteúdo geográfico complexo, guardar os locais visitados e partilhá-los com outros utilizadores. A utilização do software R.e.C. permitirá a visualização das formas geométricas das áreas em geral.

14. Meios para a execução: Computadores com acesso à Internet e o programa R.e.C. instalado. “ Data show”. Acesso a net.

15. Avaliação: A avaliação do processo consiste na auto-avaliação e/ou avaliação mútua. A avaliação dispensa qualquer processo formal, tais como: nota, exames, etc.. Além do mais, neste processo, tanto o professor quanto o aluno saberão suas dificuldades e, também seus progressos. O professor pode observar a evolução do aluno, isto é, se ele construiu seu conhecimento com relação ao que se propõe.

16. Cronograma: O projeto foi elaborado para ser executado num determinado bimestre escolar, estimando-se as datas da seguinte maneira: 1º. Encontro – Apresentação de slides e vídeos e discussões informais para destacar a importância da trigonometria no nosso dia-a-dia. 2º. Encontro – Divisão dos grupos para pesquisa dos tópicos pré-determinados. 3º. Encontro – Cada grupo deverá expor suas dúvidas e observações a respeito dos itens que estão sendo pesquisados. 4º. Encontro – Debates sobre os resultados das pesquisas realizadas, as críticas e possíveis sugestões. 5º. Encontro – Apresentação dos tutoriais do software R.e.C. e manipulação de suas funções primárias. 6º. Encontro – Buscas de fotos e mapas, com escalas gráficas, das regiões desmatadas para serem transpostas e se efetuarem os cálculos das áreas.

Um pouco da História da Trigonometria A origem da trigonometria é incerta. Entretanto, pode-se dizer que o início do desenvolvimento da trigonometria se deu principalmente devido aos problemas gerados pela Astronomia, Agrimensura e Navegações, por volta do século IV ou V a.C., com os egípcios e babilônios. A palavra trigonometria significa medida das partes de um triângulo. Não se sabe ao certo se o conceito da medida de ângulo surgiu com os gregos ou se eles, por contato com a civilização babilônica, adotaram suas frações sexagesimais. Mas os gregos fizeram um estudo sistemático das relações entre ângulos - ou arcos - numa circunferência e os comprimentos de suas cordas. No séc. III a.C., Arquimedes de Siracusa na sequência do trabalho que desenvolveu para calcular o perímetro de um círculo dado o respectivo raio, calculou o comprimento de grande número de cordas e estabeleceu algumas fórmulas trigonométricas. O astrônomo Hiparco de Nicéia, por volta de 180 a 125 a.C., ganhou o direito de ser chamado "o pai da Trigonometria" pois, na segunda metade do século II a.C., fez um tratado em doze livros em que se ocupou da construção do que deve ter sido a primeira tabela trigonométrica, incluindo uma tábua de cordas. Evidentemente, Hiparco fez esses cálculos para usá-los em seus estudos de Astronomia.

CONTINUAÇÃO Na antiguidade, o transporte e a comunicação por via terrestre envolviam enormes dificuldades, pois as vias de acesso entre as localidades eram más. Para percorrer grandes distâncias, era bem mais fácil, portanto, estabelecer rotas marítimas. A partir da necessidade de se navegar em alto mar, surgiu o problema básico da navegação: o de se determinar a posição de um navio em alto mar. Tentando resolver o problema da navegação, os gregos interessaram-se também, em determinar o raio da Terra e a distância da Terra à Lua. Este último problema implicou o surgimento das primeiras noções de Trigonometria. O primeiro cálculo da circunferência da Terra foi realizado por Erastóstenes (250 A.C.), o bibliotecário de Alexandria. Os seus cálculos dependiam do ângulo formado pela sombra do Sol e pela vertical em dois pontos: um ao norte e outro ao sul. O cálculo, feito por Erastóstenes, para a circunferência da Terra - 38400 km - foi um resultado fantástico se considerarmos os cálculos atuais cerca de 40.072 km ao longo da linha do equador. Um erro muito pequeno para uma medida tão simples, e feito há tanto tempo!

Aplicações e Problemas para demonstrar a importância das relações trigonométricas no dia a dia. 01– Um ônibus sobe uma rampa que forma com a horizontal um ângulo de 30º. Tendo percorrido 500 m, o ônibus se encontra a que altura em relação à horizontal?

02– A figura abaixo representa um copo de 15cm de altura com um canudinho dentro. Calcule o comprimento aproximado desse canudinho sabendo que 8 cm dele está fora do copo.

03– Um pára-quedista salta de um avião quando este se encontra a 1500 m de altura. Devido à velocidade do avião e da ação do vento, o pára-quedista cai conforme indica o segmento PA, inclinado 30º em relação a PB (conforme figura abaixo). A que distância do ponto B o pára-quedista vai cair? ( 1,0 ponto )

Situações mais complicadas e interessantes, como a medição de distâncias inacessíveis. 04- Calcule a distância que o garoto deve estar de tela para que possa ver sua linha superior sob um ângulo de 30º .

05- Sob um ângulo de depressão de 10º avista-se do alto de um farol, cuja altura é de 36m, um navio. A que distância do farol se encontra tal navio? (sen 10 º = 0,17; cos 10 º = 0,99; tg 10º = 0,18)

06- Um foguete é lançado de uma rampa situada no solo, sob um ângulo de 30 º. A que altura encontra-se esse foguete após percorrer 8 km?

Questão 07 Primeiro momento : Na tela aparecerá uma ação com o carro de bombeiro se posicionando próximo ao prédio, mantendo-se fixo. A escada estará travada em um ângulo de 30 graus. O aluno terá que encontrar o comprimento da escada, que ele vai precisar para alcançar o prédio em cada altura descrita na tabela ao lado, e a distância que o carro estará do prédio. Aparecerá um feedback se o aluno errar a resposta aparecerá a seguinte mensagem : “Estude mais pois este não é o resultado”. Se ele acertar aparecerá “Parabéns você é um grande matemático”, assim ele poderá encontrar a próxima distância do carro ao prédio e o comprimento da escada. Segundo momento : Após o primeiro momento o aluno terá que discutir com os colegas e responder as questões abaixo e em seguida fazer um relatório: Discuta com seus colegas e anote os comentários. Qual o comprimento da escada que você precisou para alcançar o primeiro andar que está em chamas? E no 2°? E no 3°? Em cada andar que está em chamas qual é a distância do carro em relação ao prédio? Que razão trigonométrica você percebeu ao realizar essa atividade?

08- Numa fazenda o galpão fica 50 m distante da casa. Sejam x e y , respectivamente, as distâncias da casa e do galpão ao transformador de energia, conforme a figura abaixo. Calcule o valor de x + y em função de  e  .

09- A água utilizada na casa de um sítio é captada e bombeada do rio para uma caixa-d’água a 50 m de distância. Sabemos que o ângulo formado pelas direções (caixa d’água-casa) e (casa-bomba) é de 45º e que o ângulo formado pelas direções (bomba-caixa d’água) e (caixa d’água-casa) é de 60º. Se pretendermos bombear água do mesmo ponto de captação até a casa, quantos metros de encanamento são necessários?

10- Deu cupim no pé da árvore e agora, infelizmente, será preciso derrubá-la. Antes, os bombeiros deverão estimar sua altura para saber se, na queda, ela não atingirá as casas vizinhas.

11- Para obter a altura do morro, os técnicos mediram os ângulos OÂT e a distância AB, como mostra a figura. a) Represente por y a medida desconhecida de OA. Escreva uma fórmula relacionando x com y. Informação: tg 35º = 0,70. b) No triângulo retângulo BOT, temos: Agora são duas equações relacionando as incógnitas x e y. Resolva esse sistema e encontre a altura do morro.

12- Considere estes pontos A, B e C na malha quadriculada: Vamos ligar A com B e B com C: Será que os pontos A, B e C estão sobre uma mesma reta? Para responder, considere os triângulos ABM e BCN:

Razões trigonométricas 13- No triângulo isósceles ABC sabe-se que AB = AC = 7 cm e BC = 6 cm. a) Desenhe o triângulo ABC (basta um rascunho, sem precisão) e trace a altura AM do triângulo. b) Calcule a medida de AM. c) Calcule sen , cos e tg . d) Consulte a tabela das razões trigonométricas e faça uma estimativa para o ângulo . e) Qual é a medida aproximada do ângulo desse triângulo?

14- O trapézio da figura tem um eixo de simetria. a) Desenhe a altura AH, perpendicular à base DC, e calcule sua medida. b) Calcule a área do trapézio. c) Descubra as medidas aproximadas dos ângulos do trapézio. Para isso, calcule alguma razão trigonométrica e consulte a tabela.

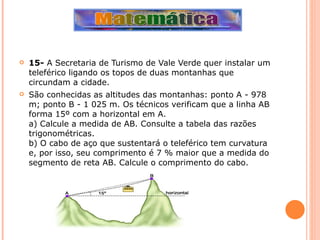
15- A Secretaria de Turismo de Vale Verde quer instalar um teleférico ligando os topos de duas montanhas que circundam a cidade. São conhecidas as altitudes das montanhas: ponto A - 978 m; ponto B - 1 025 m. Os técnicos verificam que a linha AB forma 15º com a horizontal em A. a) Calcule a medida de AB. Consulte a tabela das razões trigonométricas. b) O cabo de aço que sustentará o teleférico tem curvatura e, por isso, seu comprimento é 7 % maior que a medida do segmento de reta AB. Calcule o comprimento do cabo.

Polígonos inscritos e circunscritos 16- Na figura, as seis circunferências têm raios iguais, e o triângulo que as envolve é eqüilátero. Calcule o lado l do triângulo em função do raio r dessas circunferências. Comece percebendo algumas relações:

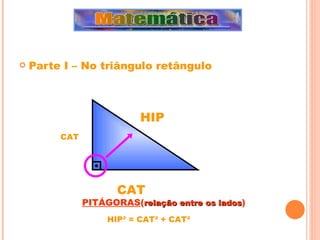
Parte I – No triângulo retângulo CAT HIP CAT PITÁGORAS ( relação entre os lados ) HIP² = CAT² + CAT²

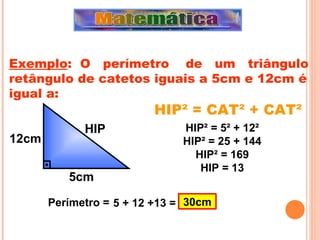
HIP² = CAT² + CAT² Exemplo : O perímetro de um triângulo retângulo de catetos iguais a 5cm e 12cm é igual a: 12cm 5cm HIP HIP ² = 5² + 12² HIP² = 25 + 144 HIP² = 169 HIP = 13 5 + 12 +13 = 30cm Perímetro =

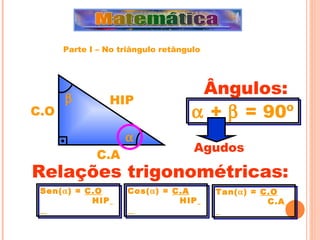
HIP C.O C.A    +  = 90º Ângulos: Agudos Sen(  ) = C.O HIP Cos(  ) = C.A HIP Tan(  ) = C.O C.A Relações trigonométricas: Parte I – No triângulo retângulo

HIP² = CAT² + CAT² Exemplo : No triângulo retângulo abaixo o valor do Cos(  ) é igual a: X 10cm 8cm 10 ² = 8² + x² 100 = 64 + x² 36 = x² x = 6 Cos(  ) =  HIP C.O C.A Parte I – No triângulo retângulo

Arcos Notáveis Parte I – No triângulo retângulo

Exemplo : Um escada de 12m de comprimento esta apoiada em um prédio fazendo com este um ângulo de 60º. A altura do prédio é: h Sen(30º) = 30º HIP C.A 12m 60º   2h=12  h=6m Parte I – No triângulo retângulo

Logo: 2cm 4cm  = 60º cos(  ) =  HIP C.A Exemplo : No triângulo retângulo abaixo o valor do ângulo  é igual a: Parte I – No triângulo retângulo

Construção do teodolito Material: -Pote redondo com tampa (o pote deve possuir movimento circular fixado a tampa); -Canudo oco em formato cilíndrico reto (o buraco interno deve ter o diâmetro de forma que seja possível visualizar o outro lado); -O desenho de um transferidor (uma cópia de um transferidor de 360°); -Madeira ou papelão que caiba a imagem do transferidor; -Tabela da tg; -cola; -arame de comprimento maior que o diâmetro do transferidor. Montando o seu Teodolito - Recorte o transferidor e fixe-o na madeira; - Fure a parte superior do pote com o arame e deixe aparecendo igualmente dos dois lados; - Cole o pote de cabeça para baixo no meio do transferidor, fixe o canudo paralelamente ao arame em cima do pote

Como se usa: Posiciona o teodolito caseiro de modo que a sua base fique perpendicular ao objeto que vamos medir a altura. Medimos a distância do objeto até o teodolito com um metro. Através do canudo, miramos o pico do objeto (o ponto mais alto), com isso o arame marcará um ângulo no transferidor. Com esse ângulo usamos a trigonometria para medir a altura. (tangente do ângulo é igual ao cateto oposto (altura) dividido pelo cateto adjacente (distância do objeto ao teodolito) Obs.: link para um vídeo sobre a utilização do teodolito na medição de distâncias inacessíveis. Distância Inacessíveis http://novotelecurso.blogsp...

Associação entre os triângulos retângulos e as tabelas trigonométricas A verificação, usando o software ReC da expressão do seno da soma

Aplicação na Medicina Trigonometria de olho na sua pressão JOSÉ LUIZ PASTORE MELLO A palavra trigonometria vem do grego e significa medida (metria) em triângulos (trigon). De fato, a trigonometria se ocupa dos métodos de resolução de triângulos, contudo, seu campo de estudo também abrange a investigação e uso das funções trigonométricas. Veremos a seguir uma aplicação desse nobre uso da trigonometria. Muitos fenômenos físicos e sociais de comportamento cíclico podem ser modelados com auxílio de funções trigonométricas, daí a enorme aplicação do estudo desse conteúdo em campos da ciência como acústica, astronomia, economia, engenharia, medicina etc. Um exemplo de relação que pode ser modelada por uma função trigonométrica é a variação da pressão nas paredes dos vasos sangüíneos de um certo indivíduo em função do instante de coleta dessa medida. O gráfico indicado abaixo representa uma investigação desse tipo onde se analisa a situação clínica de um paciente, sendo P a pressão nas paredes dos vasos sangüíneos (em milímetros de mercúrio: mmHg) e t o tempo (em segundos). Em geral, a pressão indicada no gráfico obedece um ciclo, sendo que cada ciclo completo equivale a um batimento cardíaco. Note por meio do gráfico que ocorre um ciclo completo a cada 0,75 segundos, o que implica dizer que a frequência cardíaca do indivíduo avaliado é de 80 batimentos por minuto. Usando a função cosseno para modelar a regularidade retratada pelos dados, podemos encontrar sua formulação a partir do gráfico. Sabendo que a função f(t)=cos t tem domínio real e imagem [-1,1], as transformações do seu gráfico necessárias para que ele modele os dados do nosso problema são: 1) modificação do período de 200 para 800/3, gerando a função f(t)= cos (800t/3); 2) reflexão de f pelo eixo t, gerando a função f(t)=-cos (800t/3); 3) modificação da imagem para [-20,20], gerando f(t)=-20cos (800t/3); 4) translação vertical do gráfico de 100 unidades, gerando a função final f(t)=100-20cos (800t/3).Usando essa função, podemos encontrar, por exemplo, a pressão após 2 segundos calculando o valor de f(2), que você poderá fazer como exercício (resposta: 110 mmHg).

FIM! Contatos: [email_address] luizpaulolobo@yahoo.com.br

Projeto Trigonometria Atualizado

Mais conteúdo relacionado

Mais procurados

Destaque

Semelhante a Projeto Trigonometria Atualizado

Projeto Trigonometria Atualizado