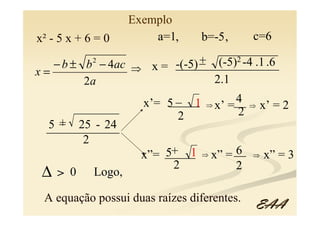
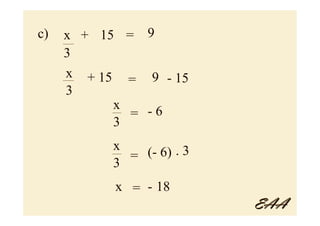O documento apresenta uma aula sobre equações algébricas do 1o e 2o grau destinada a alunos do 9o ano. Introduz o conceito de equações algébricas e explica como resolver equações do 1o grau por meio de operações algébricas básicas. Também apresenta a fórmula geral para equações do 2o grau e explica como calcular o discriminante para determinar o número de raízes.

1. Aula de álgebra destinada a alunos do 9o ano
do ensino fundamental do CEAL.
O objetivo deste trabalho, é introduzir o estudo
das equações de forma descontraída, chamando
atenção para as operações fundamentais e o uso
das letras no estudo da matemática. Observa se
ainda a evolução do aluno no decorrer de sua
formação.

2. Equações algébricas
EAA

3. Equações algébricas são equações nas quais
a incógnita x está sujeita a operações
algébricas como: adição, subtração,
multiplicação, divisão e radiciação.
EAA

4. Equação do primeiro grau
As equações de 1o grau são equações na
forma.
ax + b = 0
(1o membro) (2o membro)
Os números reais a e b são os coeficientes
da equação.
EAA

5. Resolução de equações
a) x + 8 = 15
x + 8 = 15 - 8
x = 7
b) x - 10 = 12
x - 10 = 12 + 10
x = 22
EAA

6. c) x + 15 = 9
3
x + 15 = 9 - 15
3
x
= -6
3
x (- 6) . 3
=
3
x = - 18
EAA

7. d) 2x +15 = 18
2 x +15 = 18 - 15
2x = 3
2x = 3
2
EAA

8. Equação do segundo grau
Uma equação do segundo grau na
incógnita x é da forma:
ax² + bx + c = 0
Os números reais a, b e c são os
coeficientes da equação.
EAA

9. Exemplo:
x² - 5 x + 6 = 0
Identificando os coeficientes:
ax² + bx + c = 0
a = 1
b = -5
c = 6
EAA

10. Vamos completar a tabela
Equação a b c
x² - 6x + 8 = 0 1 -6 8
x² - 10 x + 25 = 0 1 - 10 25
2x² + 4x + 14 = 0 2 4 14
x² + 1 = 0 1 0 1
- x² + 2x = 0 -1 2 0
EAA

11. Fórmula de Bháskara
−b± ∆
x=
2a
∆ (delta ) letra do alfabeto grego , usada
para representar o valor da equação:
b² - 4ac .
EAA

12. ∆ = b² - 4ac, é o discriminante da equação
2o
de grau ax2 + bx + c = 0. Onde a é o
coeficiente de x2, b é o coeficiente de x
e c o termo independente.
EAA

13. Exemplos
1. Calcule o discriminante ∆ na equação.
3x² - 3x + 6 = 0, a = 3, b = -3, c=6
∆ = b² - 4ac
∆ = (-3)2 - 4 . 3. 6
∆ = 9 - 4 . 18
∆ = 9 - 72
∆ = - 63 EAA

14. 2. Calcule o discriminante ∆ na equação.
x² + 6x + 9 = 0
a = 1, b = - 6, c = 9
∆ = b² - 4ac
∆ = (- 6)2 - 4 .1 .9
∆ = 36 - 36
∆= 0
EAA

15. 3. Calcule o discriminante ∆ na equação.
x² + 2x - 3 = 0 a = 1, b = 2, c=-3
∆ = b² - 4ac
∆ = 22 - 4 . 2 . (- 3)
∆ = 4 - 8 . (- 3)
∆ = 4 + 24
∆ = 28 EAA

16. −b± ∆
Sendo ∆ = b² - 4ac e x=
2a
Dada a equação de 2o grau.
ax2 + bx + c = 0.
temos, ∆ = b 2 − 4ac
logo, - b - b 2 − 4ac
x' =
2a
− b ± b 2 − 4ac
x=
2a
- b + b 2 − 4ac
x" = EAA
2a

17. Exemplos
a) x² - 5 x + 6 = 0 a = 1, b = -5, c=6
_ (-5)2 - 4 .1 . 6
− b ± b − 4ac ⇒ x = -(-5) +
2
__________________
x=
2a 2.1
_ 1 4
_____ ⇒ x’ = __ ⇒ x” = 2
5
x’ =
_ 25 - 24 2 2
5+
x = ____________
2
6
5 + 1 ⇒ x”= __ ⇒ x” = 3
_____
x” =
2 2
S ={2; 3} EAA

18. b) x² + 8x + 15 = 0
a = 1, b = 8, c = 15
− b ± b − 4ac
2 _
+ 82 -4 .1 .15
_________________
x= ⇒ x= -8
2a 2.1
-8 _
____ 4 ⇒ x’=-10 ⇒ x’ = -5
__
x’=
2 2
x= -8 _ 64 - 60
+
____________
2
-8 + 4 ⇒ x”= -6 ⇒ x”= -3
x”= ____ __
2 2
S ={-5; -3} EAA

19. c) x² + 6 x + 9 = 0
a = 1, b = 6, c=9
− b ± b − 4ac
2 _
+ 62 -4 .1 .9
_________________
x= ⇒ x= -6
2a 2.1
-6 _
____ 0 ⇒ x’= -6 ⇒ x’= -3
__
x’=
2 2
x= -6 _ 36 - 36
+
____________
2
____
x”= -6 + 0 ⇒ x”= __ ⇒ x”= -3
-6
2 2
S ={-3} EAA

20. d) 3 x² - x + 3 = 0
a = 3, b = -1 , c=3
− b ± b − 4ac
2 _
- (-1) + (-1)2 -4. 3 . 3
x= ⇒ x = ______________
2a 2.3
x= 1 + 1 - 36 ⇒ x= 1 _ -35 ⇒ x ∉ ℜ
_
____________ +
______
6 6
S ={ }
EAA

21. O discriminante ∆ há três possíveis situações:
1. Se ∆ > 0
há duas soluções reais e diferentes:
x’ = -b - ∆
_______ e x” = -b + ∆
_______
2a 2a
EAA

22. Exemplo
x² - 5 x + 6 = 0 a=1, b=-5 , c=6
2 _ (-5)2 -4 .1 .6
− b ± b − 4ac ⇒ x = -(-5) +
_________________
x=
2a 2.1
x’= 5 _ 1 4
_____ ⇒ x’ =__ ⇒ x’ = 2
2 2
5+_ 25 - 24
____________
2
x”= _____ ⇒ x” = __ ⇒ x” = 3
5+ 1 6
2
∆ > 0 Logo, 2
A equação possui duas raízes diferentes.
EAA

23. 2. Se ∆= 0
há duas soluções reais iguais:
−b± ∆ −b± 0
x= ⇒ x=
2a 2a
b
x' = x” ⇒ −
2a
EAA

24. Exemplo
x² + 6 x + 9 = 0 a = 1, b = 6, c=9
− b ± b − 4ac
2
⇒ -6 _
+ 62 -4 .1 .9
x = ______________
x=
2a 2.1
x’= - ____
6- 0 ⇒ x’= -__ ⇒ x’= -3
6
2 2
_
-6 + 36 - 36
____________
x=
2
x”= -____
6+ 0 ⇒ x”= -__
6 ⇒ x”= -3
2 2
∆ =0 Logo,
A equação possui duas raízes iguais. EAA

25. 3. Se ∆ <0
não há solução real, pois não existe raiz
quadrada real de número negativo.
-b± -∆
x=
2a
logo, x ∉ℜ
EAA

26. Exemplo
3 x² - x + 3 = 0 a = 3, b = -1 , c=3
− b ± b − 4ac ⇒
2 _ (-1)2 - 4. 3 .3
(-1) +
x = -_________________
x=
2a 2.3
_
+ 1 - 36
x= __________ ⇒ x = 1 +
1 _
_________ ⇒ x ∉ ℜ
- 35
6 6
∆ < 0 Logo,
A equação não possui raízes reais.
EAA

27. Exemplos
1. Determine o número de raízes na equação.
3x² - 3x + 6 = 0 a = 3, b = -3, c=6
∆ = b² - 4ac ∆= (-3)2 -4 . 3 . 6
∆= 9 - 4.18 ∆= 9 - 72 ∆= - 63
A equação não possui raízes reais.
EAA

28. 2. Determine o número de raízes na equação.
x² + 6x + 9 = 0 a = 1, b = - 6, c=9
∆ = b² - 4ac ∆ = (-6)2- 4 . 1. 9
∆ = 36 - 36 ∆ =0
A equação possui duas raízes iguais.
EAA

29. 3. Determine o número de raízes na equação.
x² + 2x - 3 = 0 a = 1, b=2, c = -3
∆ = b² - 4ac ∆ = 22- 4 . 2.(-3)
∆ = 4 - 8.(-3) ∆ = 4 + 24 ∆ = 28
A equação possui duas raízes diferentes.
EAA

30. Resolva as equações.
a) x² - 3x + 2 = 0 g) y² - 25 = 0
b) 2y² - 14y + 12 = 0 h) x² - 1/4 = 0
c) - x² + 7x – 10 = 0 i) 5x² - 10x = 0
d) 5x² - x + 7 = 0 j) 5 + x² = 9
e) 7x² - 3x = 4x + x²
f) z² - 8z + 12 = 0
EAA