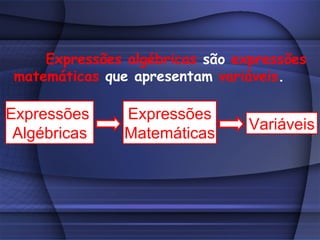
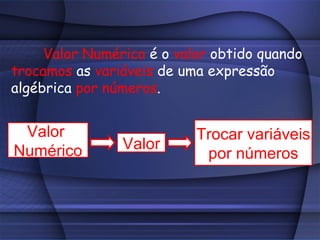
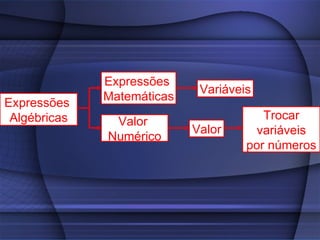
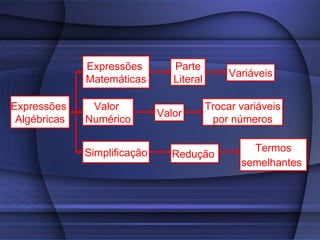
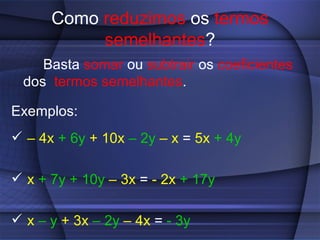
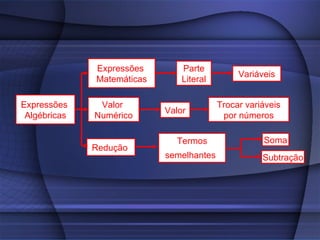
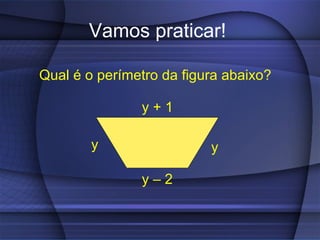
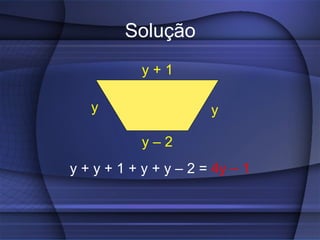
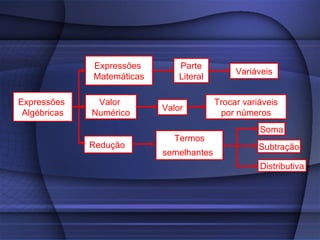
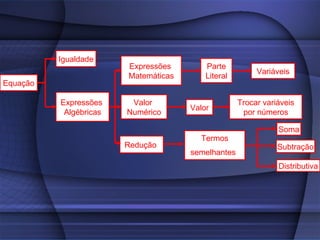
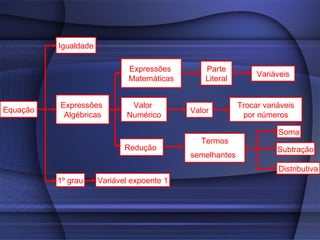
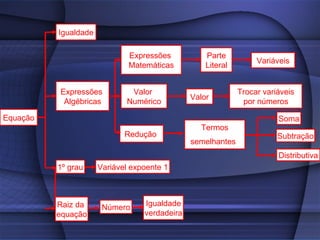
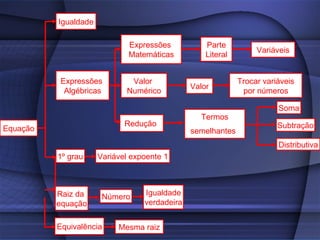
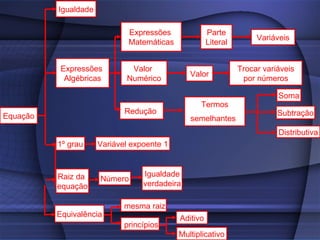
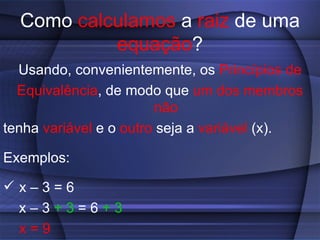
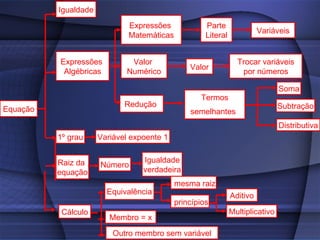
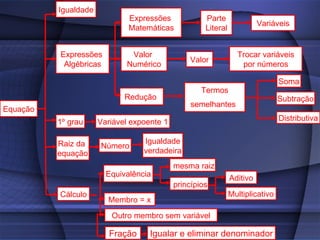
O documento fornece uma explicação detalhada sobre equações do primeiro grau, incluindo expressões algébricas, valor numérico, redução de termos semelhantes, equações, raiz de equações, princípios de equivalência e como calcular a raiz de uma equação do 1o grau.