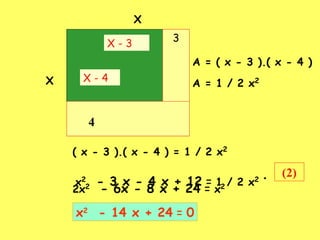
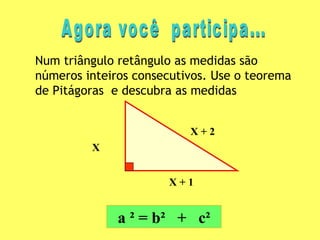
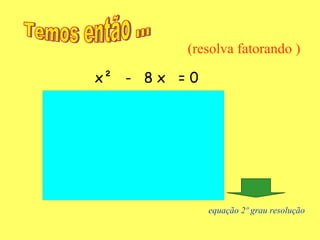
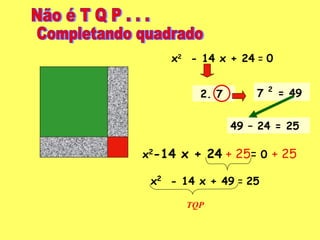
1) O documento apresenta vários problemas de equações de segundo grau, incluindo um terreno retangular, um palhaço equilibrista e um triângulo retângulo. 2) Explica como derivar as equações de segundo grau a partir dos enunciados dos problemas e como identificar os coeficientes a, b e c. 3) Demonstra como resolver as equações de segundo grau usando a fórmula de Bhaskara.

1. Prof°: Francisco Sérgio ALUNO(A) ALUNO(A) Nº Nº 1º ano Noturno:2011 E.E. Padre José Scampini Prof° Instrutor: Charles Lucas Maldonado

2. EQUAÇÃO DE 2º GRAU

3. Olha o probleminha ... Um terreno retangular em que um dos lados é 18 metros maior que o outro, tem área igual a 360 m². Quais as dimensões deste lote? x x + 18

4. Algebrizando... Área = lado x lado A = x . ( x + 18 ) Se A = 360 m 2 então x.( x + 18 ) = 360 x . ( x + 18 ) = x 2 + 18 x = 360 x 2 + 18 x – 360 = 0

5. a x 2 + b x + c = 0 a b c Coeficientes numéricos X Incógnita ou variável Equação de 2º de grau * Forma normal ou reduzida

6. Os coeficientes são: a = b = C = Os Coeficientes são iguais ou diferentes de zero ? A equação é completa ou incompleta? equação 2º grau resolução automatica.xls Na equação abaixo, x 2 + 18 x - 360 = 0

7. Olha só a do palhaço ... Um palhaço equilibrista, testando a fórmula de Galileu Galilei que é aproximadamente d = 5 t 2 , tentou atravessar em uma corda a 45 metros do chão, se ele cair em quantos segundo ele chegará a rede de proteção? Se tiver sorte é claro! d = 5 t 2 d = distância t = tempo

8. d = 5 t 2 5 t 2 = 45 5 t 2 - 45 = 0 Então os c oeficientes são: A = B = C = Coeficientes são iguais ou diferentes de zero ? Equação é completa ou incompleta?

9. Quanto tempo o palhaço levaria para chegar ao solo, digo a rede? É com você... 5 t 2 - 45 = 0 equação 2º grau resolução automatica.xls

10. Outro situação Problema... Em um quadrado de lado x, o número que expressa a área é igual ao número que expressa o dobro de seu perímetro. X X a) Qual a medida de seu lado? b) Qual é o perímetro do quadrado? c) Qual é a área do quadrado?

11. Para que um produto se anule um dos fatores deve ser igual a zero... a . b = o Então fatore e ache as soluções ... a = 0 ou b = 0

12. Então os c oeficientes são: A = B = C = Coeficientes são iguais ou diferentes de zero ? Equação é completa ou incompleta? x² - 8 x = 0

13. Temos então ... x² - 8 x = 0 (resolva fatorando ) equação 2º grau resolução automatica.xls

14. Agora você participa... Num triângulo retângulo as medidas são números inteiros consecutivos. Use o teorema de Pitágoras e descubra as medidas X X + 2 X + 1 a ² = b² + c²

15. Reduza a forma geral e obtenha os números: equação 2º grau resolução automatica.xls X X + 2 X + 1

16. Veja só este problema ... Um velho aposentado teve parte de seu terreno desapropriado pela prefeitura, que pretendia alargar duas avenidas. Do terreno em forma de um quadrado, foram perdidas uma faixa de quatro metros ao sul e uma faixa de 3 metros de largura ao leste. A área do terreno ficou reduzida à metade. Quais as dimensões originais do terreno?

17. X X 3 4 X - 3 X - 4 A = ( x - 3 ).( x - 4 ) A = 1 / 2 x 2 ( x - 3 ).( x - 4 ) = 1 / 2 x 2 x 2 - 3 x - 4 x + 12 = 1 / 2 x 2 . x 2 - 14 x + 24 = 0 2x 2 - 6x - 8 x + 24 = x 2 (2)

18. x 2 - 14 x + 24 = 0 2. 7 7 2 = 49 49 – 24 = 25 x 2 -14 x + 24 + 25 = 0 + 25 x 2 - 14 x + 49 = 25 TQP Não é T Q P . . . Completando quadrado

19. TQP ( x – 7 ) 2 = 25 x – 7 = x – 7 = x – 7 = + 5 x – 7 = - 5 ou x = 12 ou x = 2 equação 2º grau resolução automática.xls Resolvendo . . . x 2 - 14 x + 24 = 0 Resolva usando a resolução automática - + - + 5

20. a x 2 + b x + c = 0 Como não é T Q P e a pode não ser quadrado Multiplique por 4a 4 a 2 x 2 + 4 ab x + 4 ac = 4 a.0 adicione b 2 4 a 2 x 2 + 4 ab x + b 2 = b 2 - 4 ac TQP (2a x + b) 2 = b 2 - 4 ac 2a x + b = + b 2 - 4 ac Fórmula de Bháskara

21. 2a x + b = + b 2 - 4 ac 2a x = - b + b 2 - 4 ac x = - b + b 2 - 4ac 2a Fórmula resolutiva para equações do 2º grau Fórmula de Bháskara

22. fim