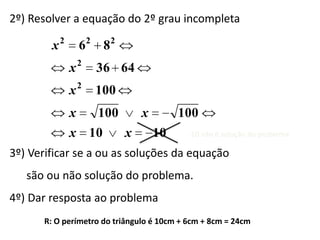
Este documento resume os principais pontos sobre equações do 1o grau. As equações do 1o grau podem ser escritas na forma ax + b = 0, com a ≠ 0. Pode-se transpor termos de um membro para outro multiplicando-os por -1. A solução é obtida fazendo x = -b/a. Exemplos ilustram como resolver equações do 1o grau passo a passo.

1. Equações do 1° Grau
Uma equação que pode ser escrita na forma ax + b = 0, onde a e b são
números reais conhecidos, com a ≠ 0, x representa uma incógnita e o
expoente de x é 1, é chamada de equação do 1° grau a uma
incógnita.
Os números conhecidos são chamados coeficientes.
Um valor que pode ser atribuído à incógnita, tal que torne a sentença
verdadeira é chamado de raiz ou solução da equação.

2. Forma Geral: ax + b = 0 a≠0
b
Solução: ax = – b x
a
Ex.: 1) 2 – 2x = 8 ⇒ – 2x = 8 – 2 ⇒ – 2x = 6 . (– 1)
⇒ x=–6/2 ⇒ x=–3
2) 2x-7 = 4x+15
Solução : Transpondo, resulta 2x-4x=7+15, isto é,
-2x = 22. Dividindo por (-2) ( ou seja, multiplicando por - ½)
Vem x = -11

3. Princípios Gerais para solução de equação do 1° grau
1) Numa equação podemos transpor um termo 9 isto é, mudá-lo de um
membro da equação para outro), desde que o multipliquemos por -1.
Em suma, a + b =c → a = c-b.
Com efeito, a+b=c a+b+(-b)= c+(-b)
a+0=c-b
2) Uma equação não se altera quando se multiplicam ambos os
membros por um mesmo número diferente.
Em suma, se K ≠ 0, a=b → Ka = Kb

4. Exercício Resolvidos
a) 3x [2 ( x 1)] 5x
3x [2 ( x 1)] 5 x 3x [2 x 1] 5 x
3x 2 x 1 5 x 3x x 5 x 2 1
x 3 ( 1) x 3

5. EXERCÍCIO DE FIXAÇÃO
1) 2x-[1-(x-2)] = 3
2) x + 1 = 1 - 3x
3) 3x – 3 = 3(x-1) x 3 x 2
4) O valor de x que satisfaz a equação
3x 5
2 3
a) 1 b)zero c)43/11 d)4 e)35/11
6) Dada a sentença x 1
2 (4 x) , podemos
afirmar que: 2 2
a) É falsa para todo x Є R
b) É verdadeira somente se x=0
c) É falsa para todo x Є N
d) É verdadeira para todo x Є R
e) É falsa para x=0

6. Equação tipo “produto” ou “quociente”
Definição
a
São equações dos tipos a.b =0 (produto) ou 0 (quociente), com {a;b}
está contido em R b
Resolução
Ao resolver equações destes tipos, lembrar-se das duas seguintes equivalências:
a.b 0 a 0 ou b 0
a
0 a 0 ou b 0
b

7. Exemplo
Resolver a equação
( x 1)(x 3)
x³ 2 x 3
(x 1)( x 3)
0 ( x 1)( x 3) 0
x³ 2x 3
x³ 2x 3 0 ( x 1 0 ou x 3 0)
x³ 2x 3 0 ( x 1 ou x 3)
x³ 2 x 3 0 x 3 V {3}

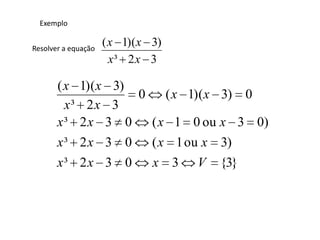
8. Exercício de fixação
1.3x – [2 – (x – 1)] = 5x
2.3(x – 2) – x = 2x – 6
3.2(x – 7) = x – (2 – x)
4.(x² + 1)(x – 1)(x + 1)=0

9. Equações do 2º grau.
Professor :Alexandre da Silva Bonifácio

10. Uma equação pode ser escrita na forma ax² +bx + c = 0 , onde a, b e c
são números reais conhecidos, com a ≠ 0 e x representa uma
incógnita, é chamada de equação do 2º grau a uma incógnita.
2
ax bx c 0 a 0

11. Exemplos
x x 3 2 2x2 1
x2 2x2 3x 2 1 0
x2 3x 3 0 É uma equação
do 2º grau
x2 3x 2 2x2 1
2 2
2x 5x 3 2x 5x 3 0

12. Exemplo
3x2 4x 5x x 2
1 x2
2 2
2 2
3x 4x 5 x 10 x
1 x2
2 2
3 x 2 4 x 2 5 x 2 10 x 2 x 2
2 2 2
3x 5x 2x 4 x 10 x 2 0
6x 2 0 É uma equação do 1º grau

13. Exemplos de equações do 2º grau:
Equação do 2º grau
completa
2
2x 4x 3 0 a=2, b=4 e c=3
2
4x 5x 0 a=4, b= -5 e c=0
2
x 36 0 a=1, b=0 e c= -36
Equações do 2º
grau
incompletas

14. Resolução de equações do 2º grau incompletas
(Revisões do 8º ano)
Caso b=0 e c≠ 0
Problema 1:
Determina o perímetro de um triângulo retângulo
de catetos 6 cm e 8 cm.
Resolução:
1º) Desenhar o triângulo retângulo
e equacionar o problema. 8
x
2 2 2
x 6 8 6

15. 2º) Resolver a equação do 2º grau incompleta
x2 62 82
x2 36 64
2
x 100
x 100 x 100
x 10 x 10 -10 não é solução do problema
3º) Verificar se a ou as soluções da equação
são ou não solução do problema.
4º) Dar resposta ao problema
R: O perímetro do triângulo é 10cm + 6cm + 8cm = 24cm

16. Exercício de Fixação
1.Resolva as equações:
a)x²- 4= 0
b) x² = 9
c) 4x² - 25 =0
d)9x² = 16

17. Resolução de equações do 2º grau incompletas
(Revisões do 8º ano)
Caso b≠o e c=0
Problema 2:
Resolver a seguinte equação, aplicando a Lei do
Anulamento do Produto:
2
x 4x 0
Recorda:
Um produto é zero se e só se um dos
seus fatores for zero. a =0 ou b=0
a b 0 a 0 b 0

18. Resolução:
1º) Fatorar o 1º membro;
2
2º) Aplicar a Lei do x 4x 0
Anulamento do
Produto; xx 4 0
3º) Resolver cada uma das x 0 x 4 0
equações do 1º grau e
determinar o x 0 x 4
conjunto-solução
C .S. 0, 4

19. Exercício de Fixação
1.Resolva as equações:
a)x²- 2x= 0
b) x² +5x = 0
c) 3x² - x =0
d)- x²+4x = 0
e)-2x² - 7x = 0

20. Exercício Propostos
a) 3x²-x-2 = 0
b) 6x²-x-1 = 0
c) x²- 5x + 6 = 0
d) 6x²-13x+6 = 0
e) 2x²- 6x = 0
f) 3x²+ 12x = 0
g) x²- 49 = 0
2) A maior raiz da equação -2x²+ 3x + 5 = 0 vale
a) -1 b)1 c)2 d)2,5 e)

21. Propriedade das raízes
a) Sejam x’ e x’’ as raizes reais da equação ax² + bx + c = 0, com a ≠ 0; sejam
ainda, S e P a soma e o produto dessas raízes, respectivamente.
Pode-se demonstrar que:
b
S x' x' '
a
c
P x '.x ' '
a
b) Obtenção de uma equação a partir das suas raízes
x² Sx P 0

22. a) Determinar a soma e o produto das raízes da equação 3x² - 15x - 2 0
Resolução
-b ( 15)
Lembrando que a 3, b -15 e c -2, a soma S 5
a 3
c 2
e o produto P
a 3
2
Resposta S 5 e P
3
1
b) Obter uma equação do 2º grau cujas raízes são 2 e
3
Resolução :
De acordo com a teoria apresentad temos :
a,
1 1 7 2
x² - (2 ) x ( 2. ) 0 x² x 0
3 3 3 3
multiplica ndo por 3 toda equação temos
3x ² 7x 2 0

23. Utilizando as propriedades da soma e produto da raízes, determinar os valores
de m na equação 2x² - 24x + 2m – 1 =0 para que:
a) uma raiz seja o dobro da outra
resolução :
Sejam as raizes x1 e x 2 as raízes e x 2 2 x1
Então :
24
x1 x2
2
x2 2 x1
substituindo x2 da 2ª equação na 1ª temos :
12
x1 2 x1 12 3 x1 12 x1
3
x1 4 e x2 8
Portanto :
2m 1 2m 1
P x1 .x2 4. 8
2 2
2m 1 32.2 2m 1 64 2m 64 1
2m 65
65
m
2

24. Exercício de Fixação
a) Para que a soma das raízes da equação (K-2)x² - 3Kx + 1= 0
seja igual ao seu produto devemos ter :
1 1 1 3
a)k b)k c)k d)k 3 e)k
3 3 3 3
b) Se m e n são raízes da equação 7x² + 9x + 21=0 então (m + 7)(n + 7) vale:
a)49 b)43 c)37 d)30 e) 30/7