O documento aborda a metodologia de ensino de trigonometria em triângulos retângulos, incluindo materiais e objetivos para a aula. Propõe atividades práticas para a compreensão das razões trigonométricas e a resolução de problemas, como o cálculo de distâncias. Também recomenda o uso de tecnologias como o GeoGebra para reforçar os conceitos aprendidos.

1. TRIGONOMETRIA no triângulo retângulo UMA SUGESTÃO DE AULA PROF.:ODILTHOM ES ARREBOLA

2. TRIGONOMETRIA Material Necessário aos alunos : Compasso, régua, esquadros e transferidor. Lápis, borracha e papel para fazer anotações. Materiais concretos papel milimetrado, papéis coloridos A4, palitos de sorvete, canudos para refrigerantes, babante; Calculadora.

3. TRIGONOMETRIA Objetivos Interpretar e fazer uso de modelos para a resolução de problema trigonométricos. Relacionar conceitos. Desenvolver a capacidade de resolver problemas por meio de alguns modelos. Construir conceitos de triângulo retângulo e a sua praticidade, para cálculo de distância. Reconhecer propriedades do triângulo. Reconhecer a utilização da razão trigonométrica no triângulo.

4. TRIGONOMETRIA Atividade do objeto de aprendizagem: Aulas para discussões sobre os conceitos vistos e algumas questões. O aluno deverá ter conhecimento de ângulo, das relações entre os ângulos e lados do triângulo retângulo e de suas razões .

5. TRIGONOMETRIA AULA 01-Calcular distâncias utilizando relações trigonométricas de umtriângulo retângulo . Material 3 folhas coloridas(cores diferentes) A4 Calculadora Giz e lousa Régua, esquadros e compasso. Mostres aos alunos o invólucro do pacote que contém as folhas A4.

6. TRIGONOMETRIA Finalidade: Perceber que a folha A4 corresponde a um retângulo cujas medidas são 210x297mm; Trabalhar com medidas decimais , isto é, em notação científica: 2,10x2,97dm Recordar aos alunos tudo sobre a figura quadrilátera-retângular (4 ângulos congruentes iguais a 90°-ângulo reto, lados 2 a 2 paralelos e congruentes)

7. TRIGONOMETRIA Seguir os seguintes passos: Dobrar a folha ao meio na direção do maior comprimento, vincando-a.

8. TRIGONOMETRIA Desdobrar a folha. Dobrar em uma das metades no sentido da diagonal, formando 2 triângulos retângulos. Desenhar na lousa a situação 2, nomeando o retângulo

9. TRIGONOMETRIA Dobrar , vincando a diagonal da folha inteira no sentido do maior comprimento.

10. TRIGONOMETRIA Desdobrar a folha. Mostrar que há 3 triângulos, sendo 2 retângulos e obtusângulo.

11. TRIGONOMETRIA Determinar diagonal menor (CE) e a diagonal maior (CB), aplicando o teorema de Pitágoras nos triângulos retângulos CAE e CDB. Usar a calculadora. Algebricamente

12. TRIGONOMETRIA Substituindo-se os valores, vem que:

13. TRIGONOMETRIA Visualizar as situações enumerando os lados

14. TRIGONOMETRIA Usar folhas de cores diferentes para dar maior realce à situação

15. TRIGONOMETRIA Usar semelhança entre triângulos. Montar as relações entre seus lados. Denominar dos lados do triângulo. Ressaltar que a hipotenusa é sempre o lado oposto ao ângulo reto=90°.

16. TRIGONOMETRIA Definir as relações trigonométricas obtidas .

17. TRIGONOMETRIA Usar a calculadora .

18. TRIGONOMETRIA Determinar os valores dos ângulos agudos.

19. TRIGONOMETRIA Usar a calculadora. Teclar shift e em seguida Digitar o número k , p.ex.: Apertar o sinal de igual (=), obtém-se assim 35,26780617° (graus). Premer a tecla , aparecerá no visor da calculadora 35º16º4.1 que corresponde a 35º16 ’4,1”

20. TRIGONOMETRIA Lembrar que a soma dos ângulos internos de um triângulo vale 180º.

21. TRIGONOMETRIA APLICAÇÃO Questão extraído “Matemática – Contexto e Aplicações.” DANTE São Paulo. Ed.Ática, 2002. Capítulo 14 –página 189, exercício proposto n.º 12 AA01- Para determinar a altura de uma torre, um topógrafo coloca o teodolito a 100 m da base e obtém um ângulo de 30°, coforme mostra a figura. Sabendo que a luneta do teodolito está a 1,70 m do solo, qual é aproximadamente a altura da torre? (dados sen30°=0,5; cos30°=0,87 e tg30º=0,58) R.:59,70 m.

22. TRIGONOMETRIA Primeiramente, faz-se um esboço da situação, isto é, o modelo matemático Analisando o esboço, observa-se que são conhecidos: 1(um) ângulo, o lado adjacente e se deseja calcular o lado oposto, i.e., h.

23. TRIGONOMETRIA Basta lembrar que a relação entre o LO e LA, por definição é a tangente do ângulo dado.Portanto, aplicando-se a definição, vem que

24. TRIGONOMETRIA Usando o programa GeoGebra (grátis) como complemento para reforçar tais conhecimentos

25. TRIGONOMETRIA Resolução do exercício

26. TRIGONOMETRIA REFERÊNCIAS BIBLIOGRÁFICAS : 01.BENIGNO, Barreto Filho e CLÁUDIO, Xavier da Silva.(2003) “ Matemática Aula por Aula .” Ensino Médio. 2.ª Série. 1.ª edição. Volume: 2 . São Paulo: Editora FTD. 02.DANTE, Luiz Roberto.( 2002) “ Matemática Contexto e Aplicações .” Ensino Médio. Volume Único. 1.ª edição. São Paulo: Editora Ática..

27. TRIGONOMETRIA 03.GUELLI, A.Cid, IEZZI , Gelson e DOLCE , Oswaldo.(1974) “ Trigonometria .” Volume: 5. São Paulo: Editora Moderna. 04.IEZZI , Gelson et al.( 1979) “ Aulas de Matemática .” São Paulo: Editora Atual. 05.IEZZI , Gelson.(2003) “ Fundamentos de Matemática Elementar - Trigonometria .” Volume: 3. 7.ª edição. 4.ª reimpressão. São Paulo: Editora Ática 06.TROTTA, IMENES e JAKUBOVIC .(1978) “ Matemática Aplicada .” 2.º grau. São Paulo: Gráfica Editora Hambburg LTDA.

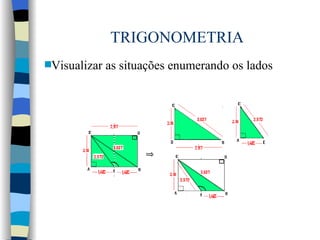
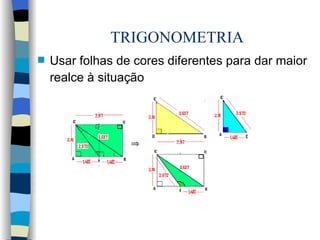
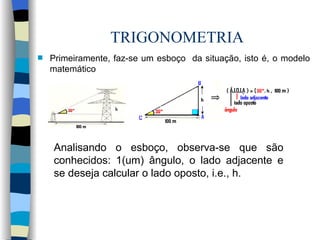
28. TRIGONOMETRIA É bom salientar que cada professor deve agir de maneira própria ao preparar suas aulas. Além disso, elas não devem ser estáticas e devem estar baseada na história espacial e temporal da classe, respeitando-se os conhecimentos prévios dos alunos. Endereços de contatos para discussão sobre o assunto: [email_address] http ://odilthom.blogspot.com/ http://twitter.com/odilthom