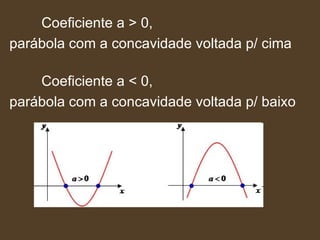
Este documento descreve as funções do segundo grau, definidas como f(x) = ax2 + bx + c. Explica que o gráfico é uma parábola que pode ter concavidade voltada para cima ou baixo dependendo do sinal de a. Detalha como encontrar as raízes, vértice e traçar o gráfico passo a passo.

1. Função do 2º Grau

2. Definição:
Toda função estabelecida pela lei de
formação
f(x) = ax² + bx + c,
com a, b e c números reais e a ≠ 0,
é denominada função do 2º grau

3. Gráfico
A representação geométrica de uma
função do 2º grau é dada por uma parábola,
que de acordo com o sinal do coeficiente a
pode ter concavidade voltada para cima ou
para baixo.

4. Coeficiente a > 0,
parábola com a concavidade voltada p/ cima
Coeficiente a < 0,
parábola com a concavidade voltada p/ baixo

5. Estudo do Gráfico de uma função
do 2º Grau:
• Raízes de uma função do 2º grau:
As raízes de uma função do 2º grau são
dadas quando fazemos y ou f (x) igual a zero,
ou seja, quando calculamos f(x)=0 encontramos
os pontos onde a função passa pelo eixo X.
Para encontrar em quais pontos a função
cruza o eixo X, formatamos a função como uma
equação do 2º Grau, encontrando as suas
raízes, utilizando o teorema de Bháskara.

6. Estudo do ∆
∆ < 0: não possui raízes reais, a parábola não
intersecciona o eixo X.
∆ = 0: possui uma única raiz real, a parábola
intersecciona o eixo X em um único ponto.
∆ > 0: possui duas raízes reais, a parábola passa
pelo eixo X em dois pontos.

7. Vértices de uma parábola
A parábola possui alguns pontos
importantes na sua análise.
Se a função possui:
a > 0 a parábola possui um ponto máximo
a < 0 a parábola possui um ponto mínimo

8. Fórmula das Coordenadas do vértice de
uma parábola: (Xv; Yv)

9. Passo a passo para traçãr o
Gráfico da Função de 2º Grau:
1º - verificar de o coeficiente a<0 ou a>0,
parábola voltada para cima ou para baixo;
2º- Igualar a função a zero e encontrar as
raízes da função (onde corta o eixo x);
3º - Encontrar as coordenadas do Vértice da
função (utilizando a fórmula).

10. Exemplo

11. Outro exemplo: