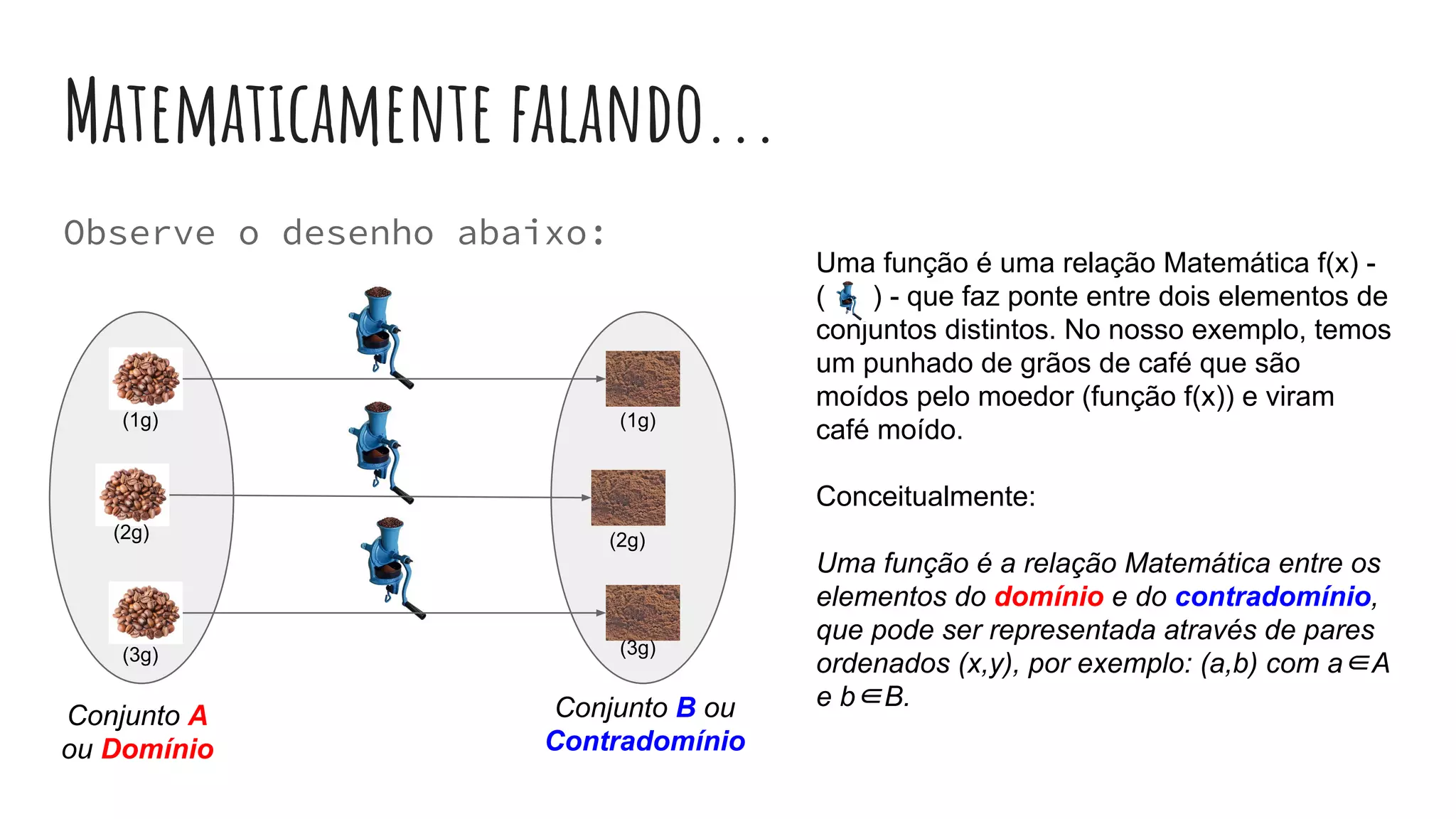
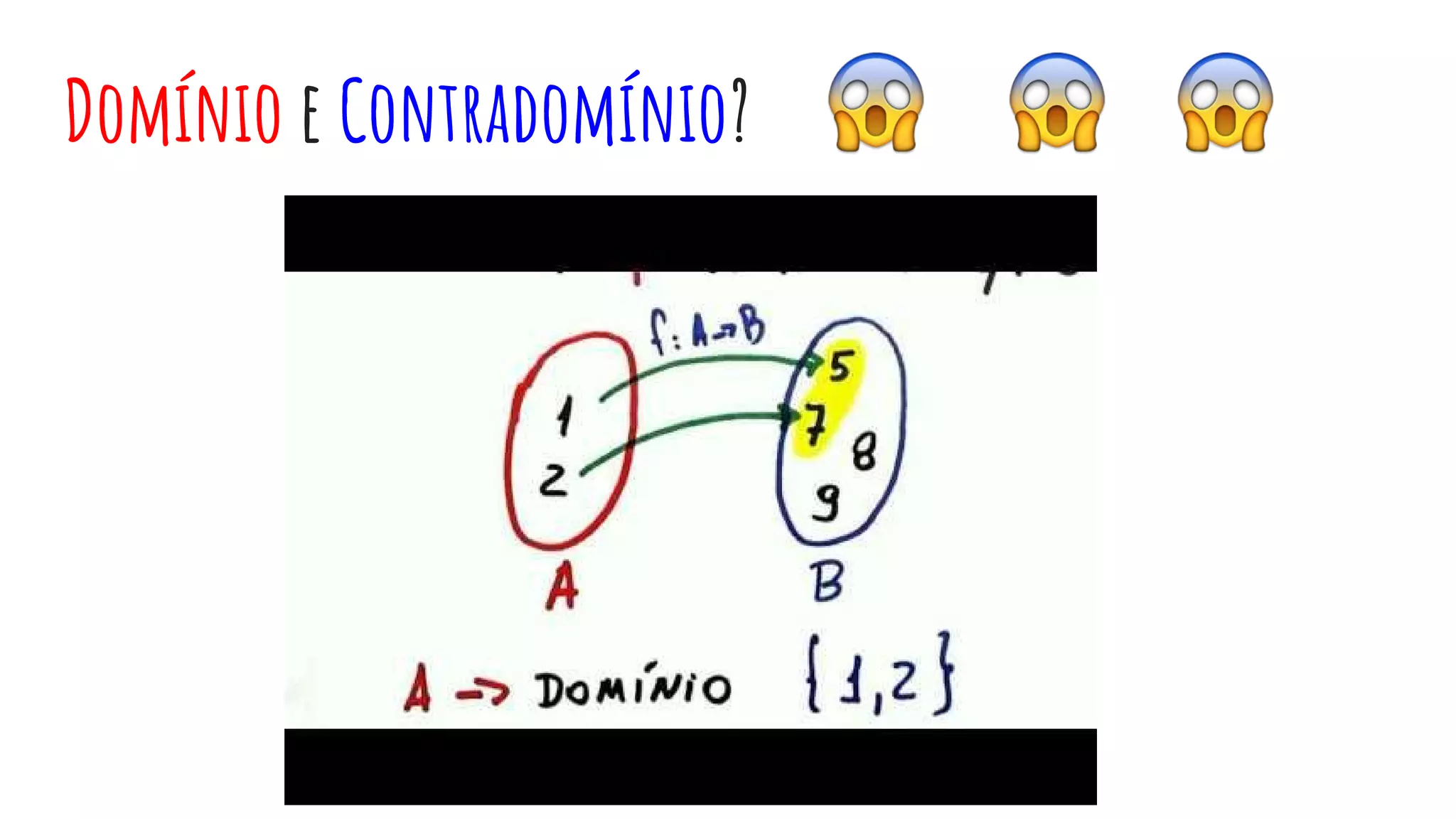
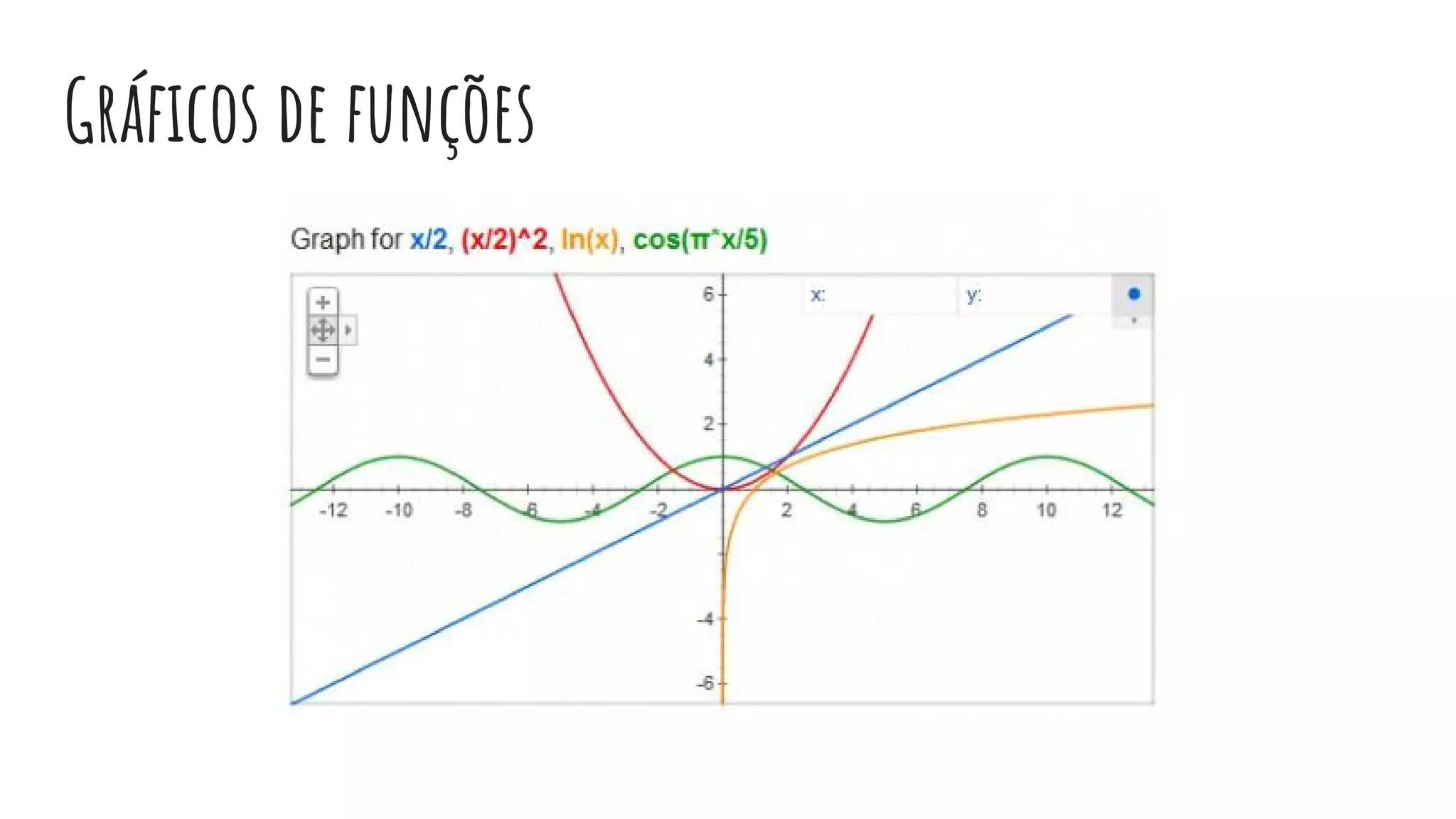
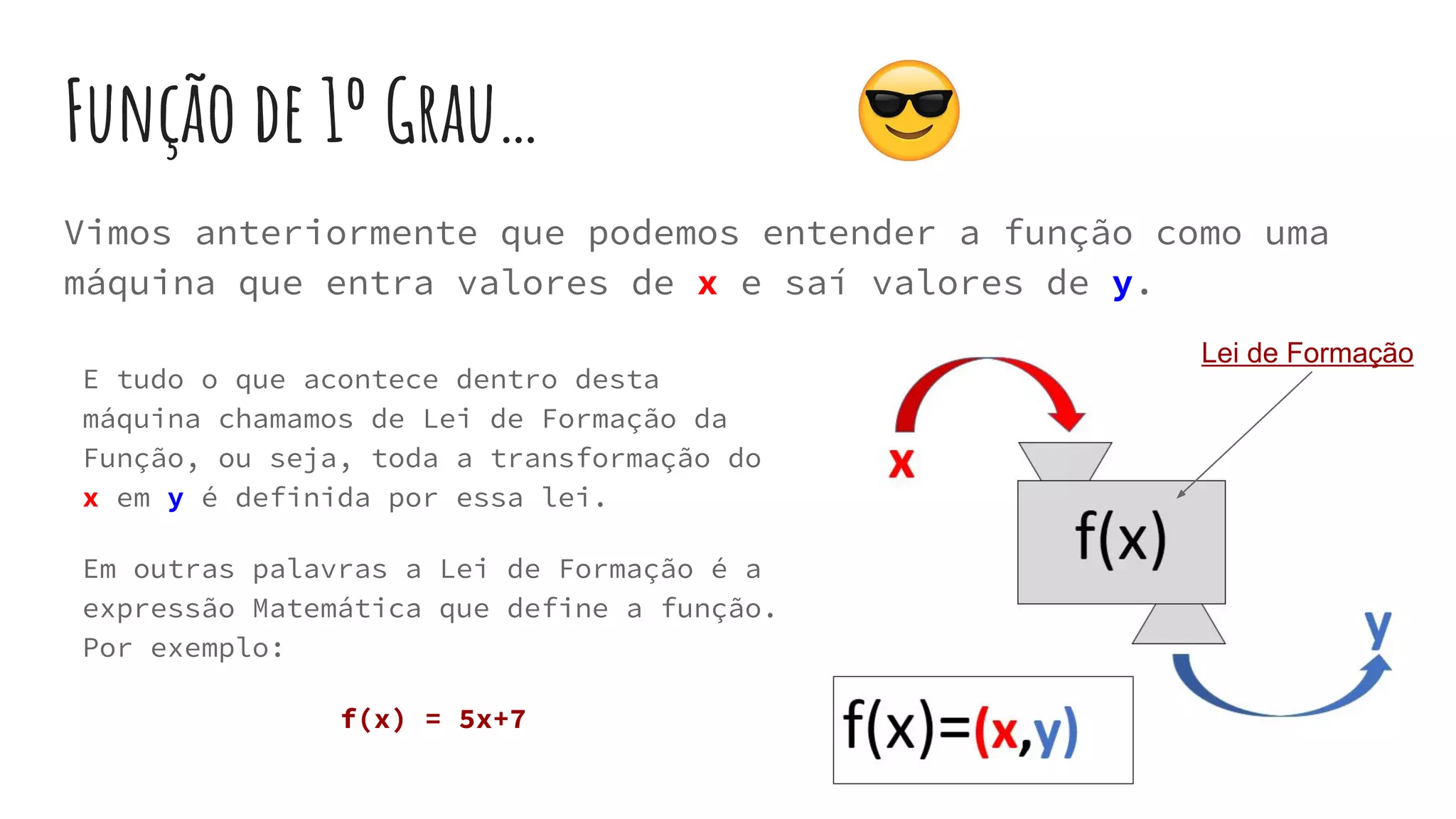
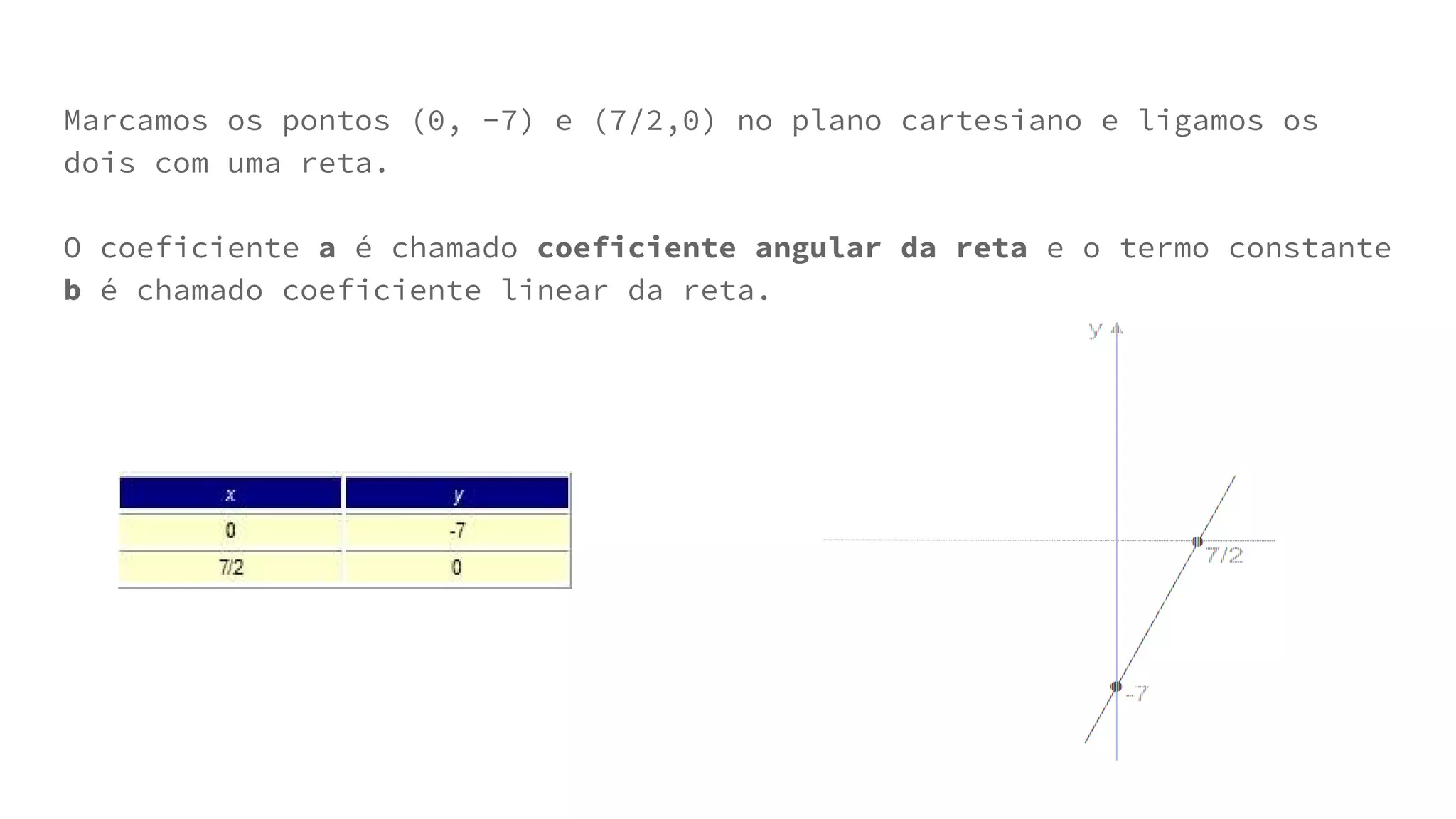
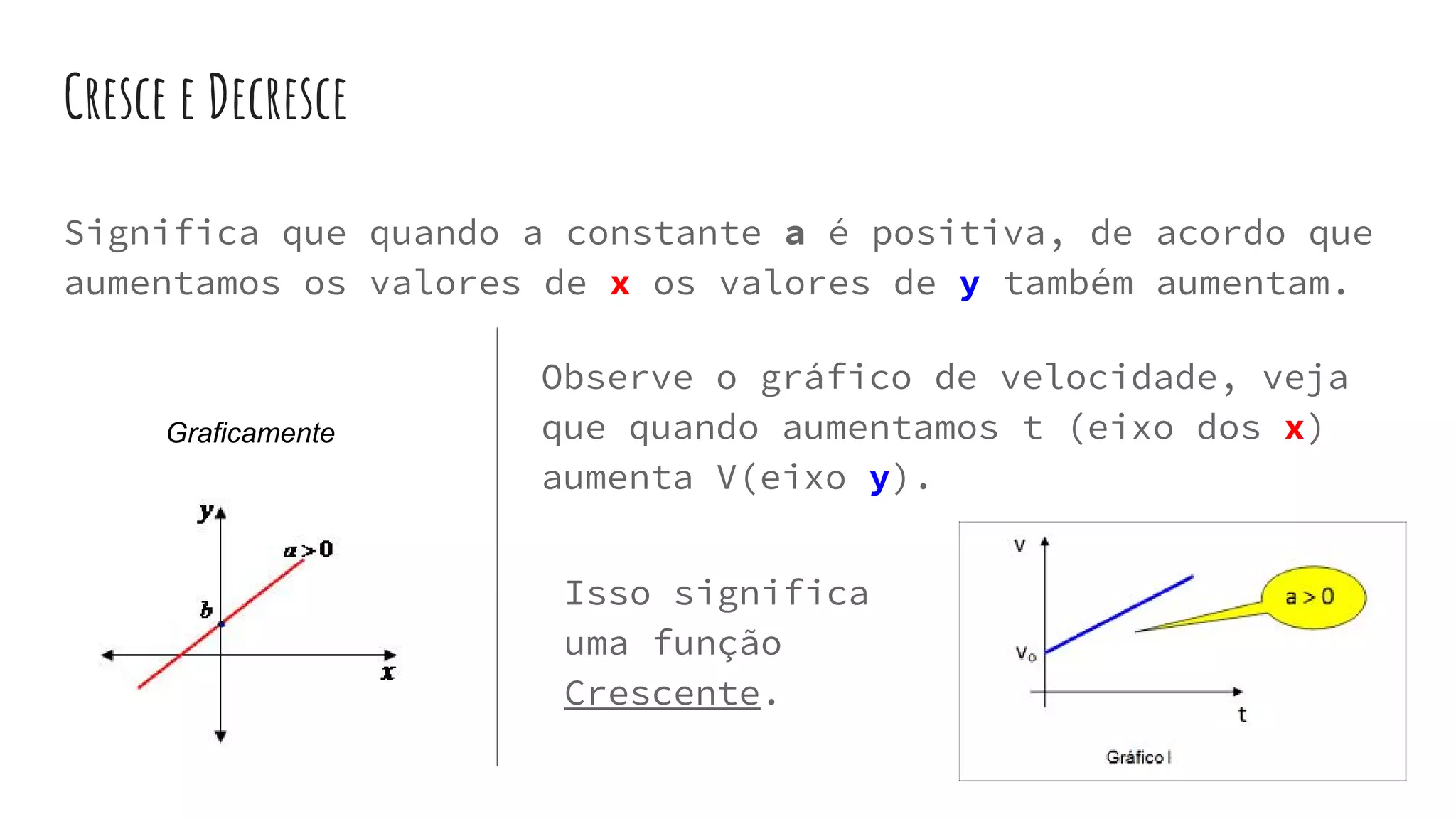
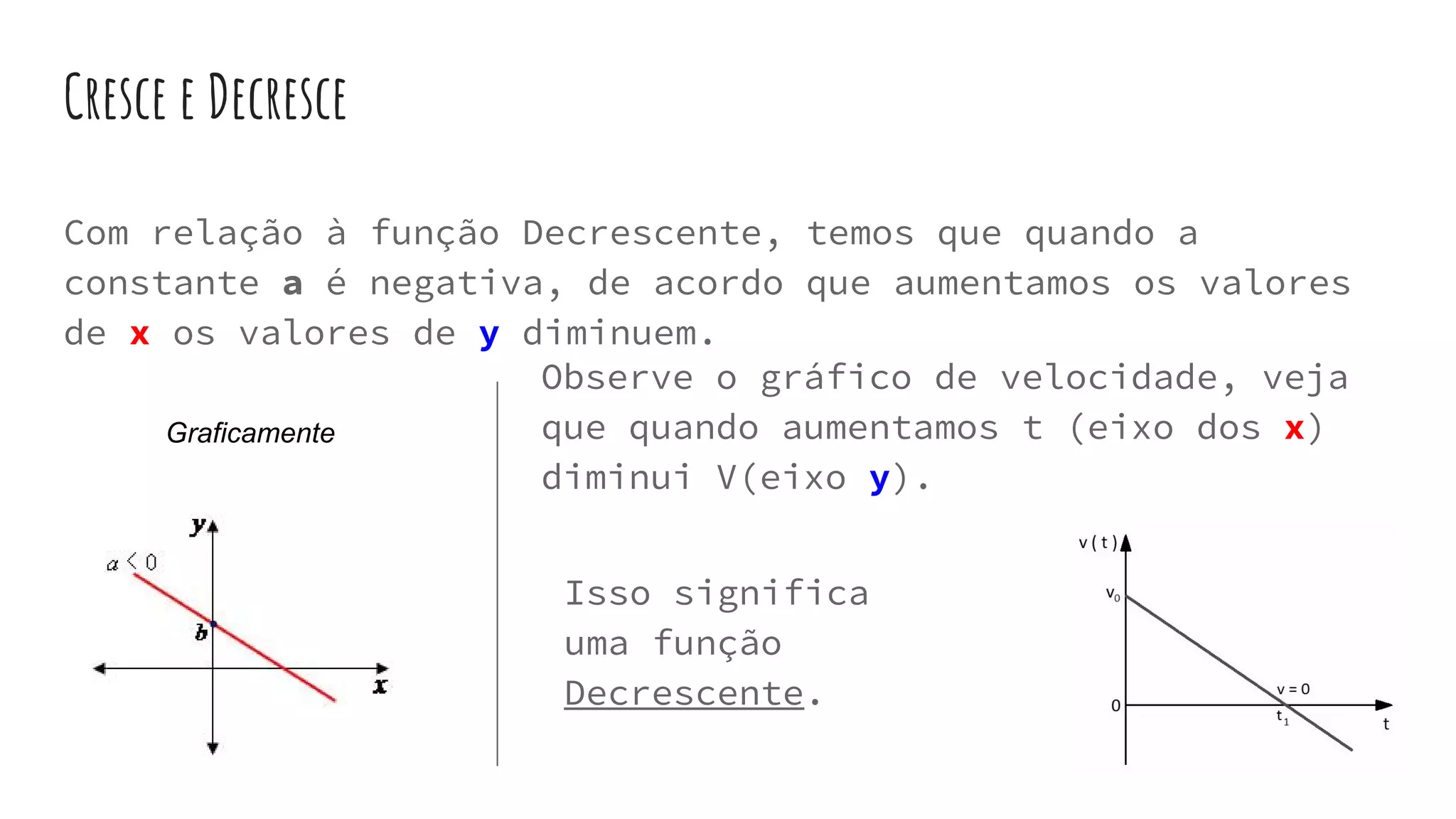
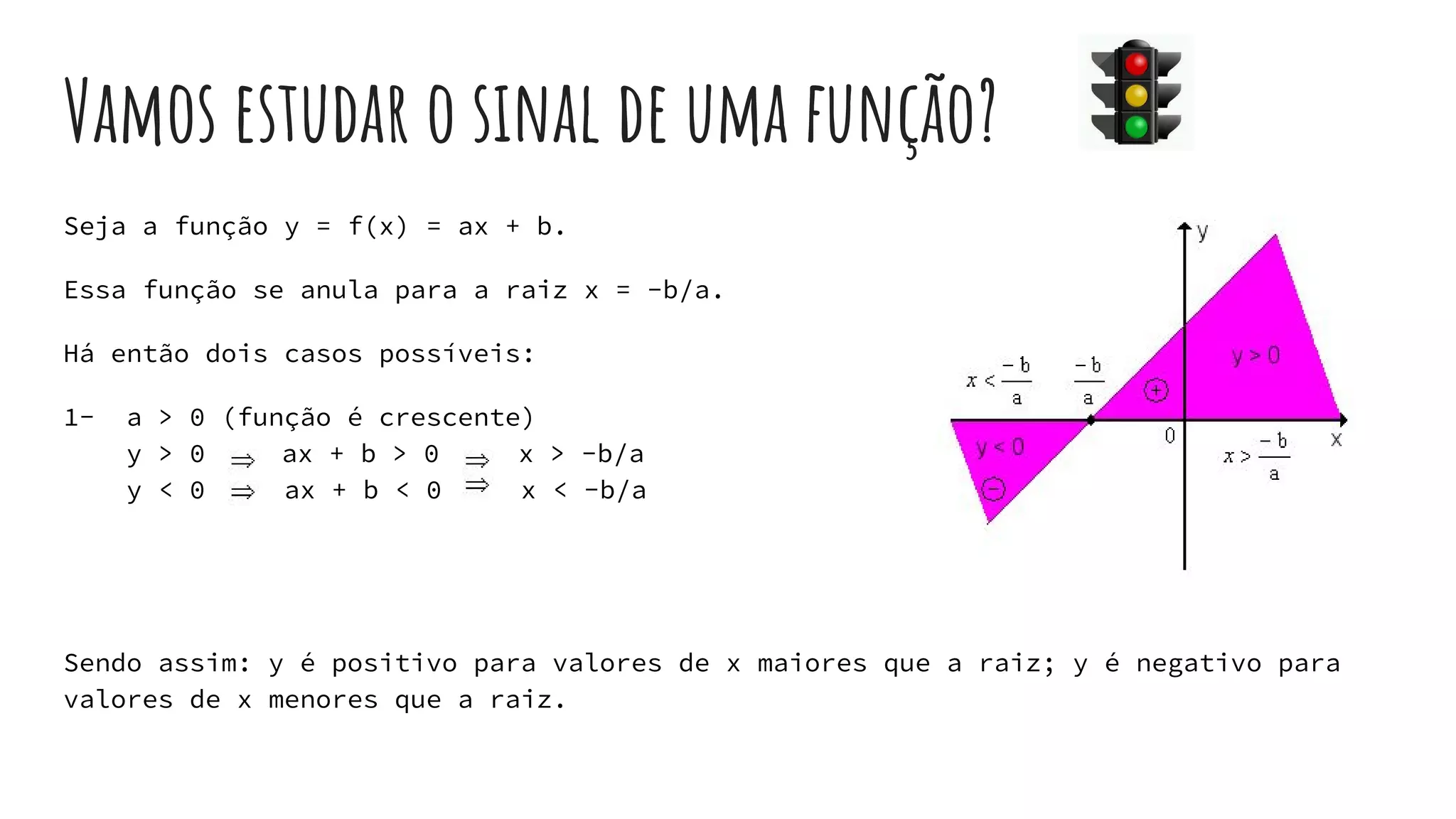
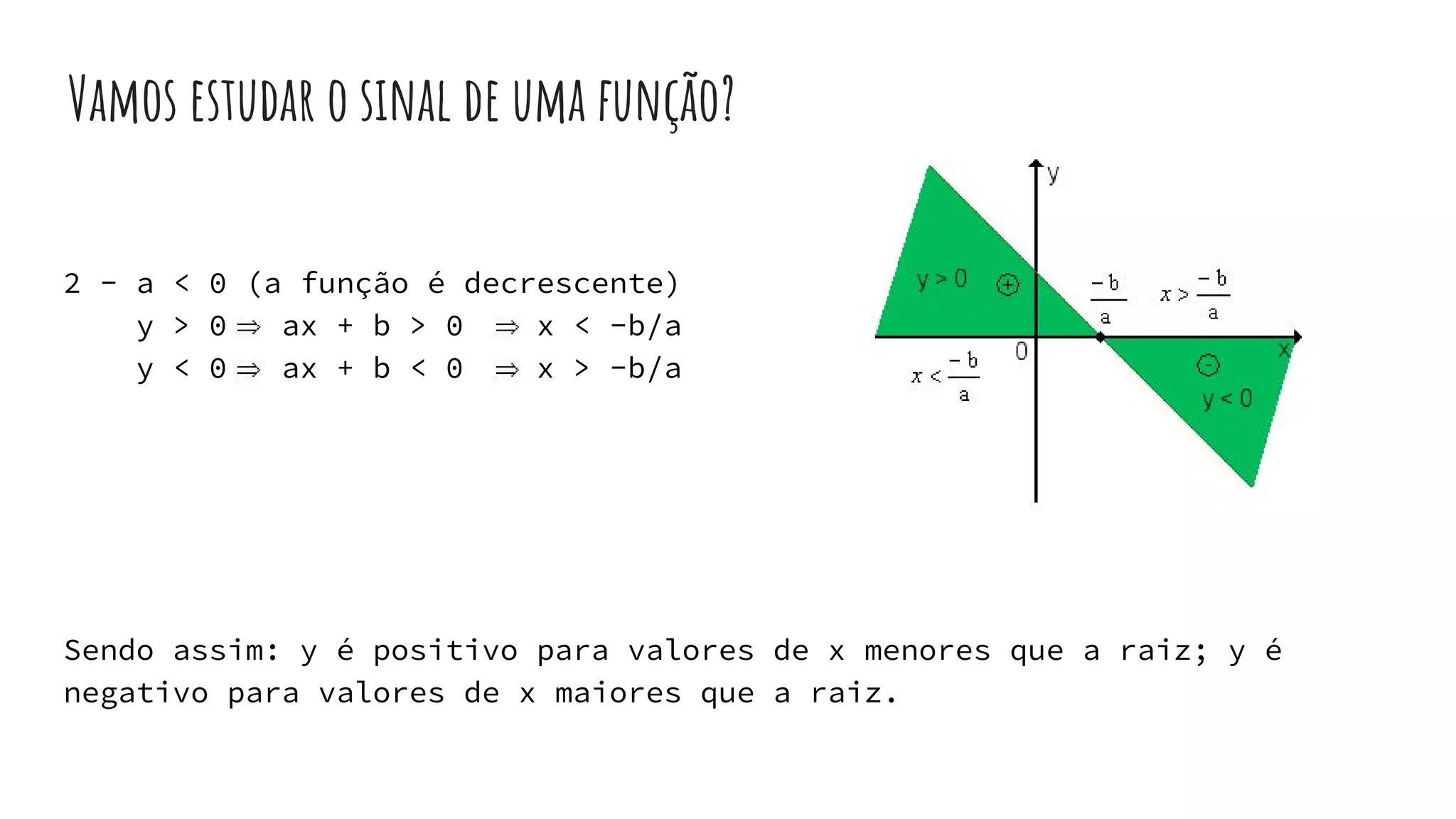
Este documento fornece uma introdução às funções de primeiro grau, definindo variáveis, domínio e contradomínio, e explicando como ler e criar gráficos de funções lineares. Explica também como calcular raízes, determinar se uma função é crescente ou decrescente, e estudar o sinal de uma função.

1. Função de 1º Grau
ESTÁ AFIM DE APRENDER?

2. Antes de continuarmos...
Antes de falarmos de função preciso saber se você sabe o que
é uma variável?
● Não!? Nunca é tarde para falarmos sobre o assunto.
Basta seguir com a apresentação.
● Sim!? Que bom, vamos rever!!!

3. Variáveis
Variáveis são grandezas que podemos mensurar, por exemplo:
● Peso;
● Altura;
● Temperatura;
● Velocidade;
● Cor dos olhos;
● Preço;
● Espaço;
● Etc.
E misturando variáveis,
criamos uma função!!!

4. Proooooonto… Podemos definir o que é uma função!
Podemos encarar uma função sendo uma máquina onde você cola
uma coisa (variável) e sai outra.
Por exemplo, a máquina de moer café:
você coloca o café em grãos e sai moído.
O moedor tem a função de moer o café.

5. Matematicamente falando...
Observe o desenho abaixo:
(1g)
(2g)
(3g)
(1g)
(2g)
(3g)
Conjunto A
ou Domínio
Uma função é uma relação Matemática f(x) -
( ) - que faz ponte entre dois elementos de
conjuntos distintos. No nosso exemplo, temos
um punhado de grãos de café que são
moídos pelo moedor (função f(x)) e viram
café moído.
Conceitualmente:
Uma função é a relação Matemática entre os
elementos do domínio e do contradomínio,
que pode ser representada através de pares
ordenados (x,y), por exemplo: (a,b) com a∈A
e b∈B.Conjunto B ou
Contradomínio

6. Domínio e Contradomínio?

7. Graus das funções
As funções podem ser divididas segundo o grau de sua
variável, por exemplo, na Função de 1º Grau o x é elevado a
potência 1, enquanto que em uma de 2º Grau o x é elevado à
potência 2, e assim sucessivamente.
● Função de 1º grau: f(x) = ax+b.
● Função de 2º grau: f(x) = ax²+bx+c…
No próximo slide são apresentados alguns tipos de gráfico.
Discuta com seu professor a que grau de função cada gráfico
pertence.

8. Gráficos de funções

9. Função de 1º Grau…
Vimos anteriormente que podemos entender a função como uma
máquina que entra valores de x e saí valores de y.
E tudo o que acontece dentro desta
máquina chamamos de Lei de Formação da
Função, ou seja, toda a transformação do
x em y é definida por essa lei.
Em outras palavras a Lei de Formação é a
expressão Matemática que define a função.
Por exemplo:
f(x) = 5x+7
Lei de Formação

10. Mas o que é então uma função de 1° grau?
Podemos definir uma função de 1° grau (também chamada de função
afim) como uma função f de IR em IR com uma lei de formação
f(x)=ax+b, com a e b números reais e a 0.
O número a é o coeficiente de x e o número b, o termo constante.
Podemos também escrever a função da seguinte forma: y = ax +b, com a
e b pertencendo aos reais e a 0.
Veja um exemplo de uma função de 1° grau:
f(x) = 2x-7, onde a = 2 e b = -7

11. Como fazer um gráfico de uma função de 1° grau?
Temos como representação gráfica da função de 1° grau uma reta.
Para a função do exemplo anterior, y = 2x-7 temos:
Definimos que o gráfico da função de 1° grau é uma reta, desta
forma obtendo dois pontos e ligando-os com uma reta teremos o
gráfico da nossa função.

12. Tive uma ideia, vamos ver um exemplo?
Se igualarmos x = 0 teremos o ponto em que a reta intercepta o eixo y.
Se igualarmos y = 0 teremos o ponto em que a reta intercepta o eixo x.
Com os ponto x e y definidos conseguiremos traçar a reta.
Para x = 0, temos y = 2 · 0 – 7 = -7. O ponto na reta é (0,-7).
Para y = 0, temos 0 = 2x - 7 = 7/2 = 3,5. O ponto na reta é (7/2,0).

13. Marcamos os pontos (0, -7) e (7/2,0) no plano cartesiano e ligamos os
dois com uma reta.
O coeficiente a é chamado coeficiente angular da reta e o termo constante
b é chamado coeficiente linear da reta.

14. Raiz de uma função???
A Raiz ou Zero de uma função é o valor do x quando o y é
zero, ou seja, quando f(x)=0 ou y=0.
Conceitualmente
falando:
Graficamente
falando:
A Raiz de uma
função é quando
a reta toca o
eixo x!
Em outras palavras, é quando a função nasce em
x!
Reta nascendo em x! Raiz da
Função

15. Para refletir!!!
Calcule o ponto em que o gráfico de f(x)=-2x+10 corta o eixo
das abscissas.

16. Cresce e Decresce
Para sabermos se uma função é crescente ou decrescente,
basta olhar o sinal da constante a.
Se na função do tipo f(x)=ax+b:
● a for maior que 0 (a>0), então a função é
CRESCENTE.
● a for menor que 0 (a<0), então a função é
DECRESCENTE.
Você deve estar se perguntando o que isto significa?

17. Cresce e Decresce
Significa que quando a constante a é positiva, de acordo que
aumentamos os valores de x os valores de y também aumentam.
Observe o gráfico de velocidade, veja
que quando aumentamos t (eixo dos x)
aumenta V(eixo y).
Isso significa
uma função
Crescente.
Graficamente

18. Cresce e Decresce
Com relação à função Decrescente, temos que quando a
constante a é negativa, de acordo que aumentamos os valores
de x os valores de y diminuem.
Graficamente
Observe o gráfico de velocidade, veja
que quando aumentamos t (eixo dos x)
diminui V(eixo y).
Isso significa
uma função
Decrescente.

19. Estudo do sinal de uma função
Nada mais é que determinar os valor de x para os quais y é
positivo, os valores de x para os quais y é zero e os valores de
x para os quais y é negativo.

20. Vamos estudar o sinal de uma função?
Seja a função y = f(x) = ax + b.
Essa função se anula para a raiz x = -b/a.
Há então dois casos possíveis:
1- a > 0 (função é crescente)
y > 0 ax + b > 0 x > -b/a
y < 0 ax + b < 0 x < -b/a
Sendo assim: y é positivo para valores de x maiores que a raiz; y é negativo para
valores de x menores que a raiz.

21. 2 - a < 0 (a função é decrescente)
y > 0 ax + b > 0 x < -b/a
y < 0 ax + b < 0 x > -b/a
Sendo assim: y é positivo para valores de x menores que a raiz; y é
negativo para valores de x maiores que a raiz.
Vamos estudar o sinal de uma função?

22. referências
AULAS DE FÍSIA. Disponível em
<http://minhasaulasdefisica.blogspot.com/2012/05/graficos-do-mruv.html>.
Acessado em 29 de Ago 2017.
BRASIL ESCOLA. Coeficiente Linear de uma Função do 1º Grau. Disponível em
<http://brasilescola.uol.com.br/matematica/coeficiente-linear-uma-funcao-1-o-g
rau.htm>. Acessado em 24 de Ago 2017.
BRASIL ESCOLA. Raiz de uma Função do 1º Grau. Disponível em
<http://brasilescola.uol.com.br/matematica/raiz-uma-funcao-1-grau.htm>.
Acessado em 29 Ago 2017.
CONCEITO.DE. Conceito de abscissa. Disponível em
<http://conceito.de/abscissa>. Acessado em 29 Ago 2017.

23. referências
CONCEITO.DE. Conceito de função. Disponível em <http://conceito.de/funcao>.
Acessado em 28 de Ago 2017.
FISMATICA. Cinemática Escalar: Aula 11 – MRUV: Gráficos. Disponível em
<http://fismatica.com.br/cinematica-aula-11-mruv-graficos>. Acessado em 29 Ago
2017.
FREEPIK. Gráficos. Disponível em
<http://br.freepik.com/fotos-vetores-gratis/punhado>. Acessado em 26 de Ago
2017.
INFOESCOLA. Raiz. Disponível em <http://www.infoescola.com/plantas/raiz/>.
Acessado em 29 de Ago 2017.

24. referências
MATIKA. Teoria função. Disponível em
<http://www.matika.com.br/funcao/definicao-de-funcao>. Acessado em 28 de Ago
2017.
ME SALVA. FUN03 - Funções - Domínio, Contradomínio e Imagem. Disponível em
<https://www.youtube.com/watch?v=Y79GQU7n95o>. Acessado em 28 de Ago 2017.
SÓ MATEMÁTICA. Função de 1º grau. Disponível em
<http://www.somatematica.com.br/emedio/funcao1/funcao1.php>. Acessado em 29 de
Ago 2017.

25. BONS ESTUDOS!
João Paulo Costa Vasconcelos
Aluno do curso de Pós-graduação Novas Tecnologias no Ensino
da Matemática (NTEM)
Universidade Federal Fluminense