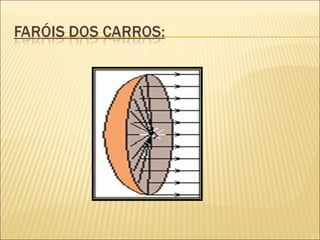
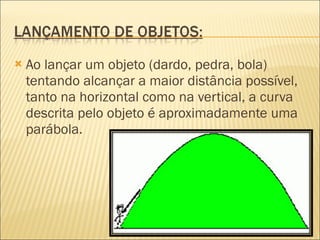
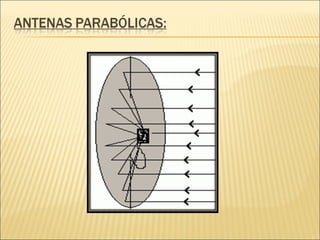
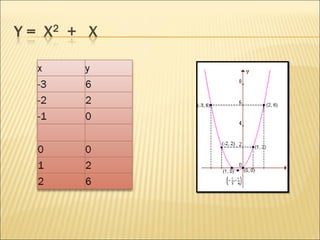
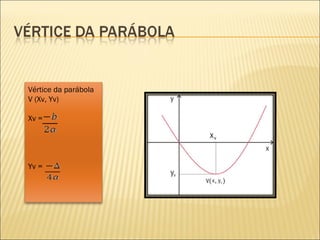
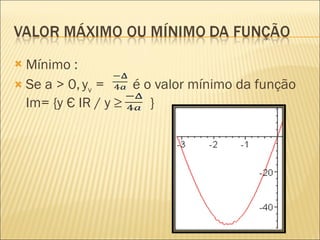
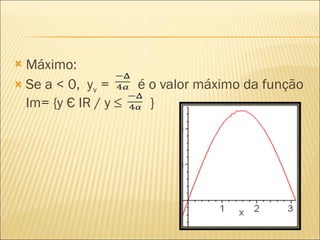
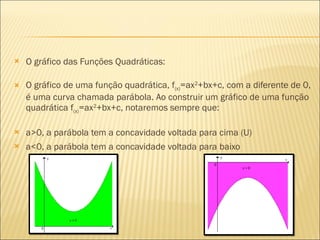
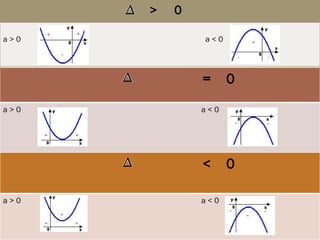
1) O documento discute parábolas, funções quadráticas e suas propriedades como vértice, raízes, domínio e conjunto imagem. 2) Uma função quadrática é dada por f(x) = ax2 + bx + c, onde a, b e c são números reais e a ≠ 0. O gráfico de uma função quadrática é uma parábola. 3) Propriedades como vértice, raízes, domínio, conjunto imagem e estudo do sinal de uma função quadrática podem ser determinados a partir de seus coeficientes a

2. No decorrer da vida existem dezenas de sítios onde encontramos parábolas, podemos até nem reparar nelas mas estão lá.

4. Ao lançar um objeto (dardo, pedra, bola) tentando alcançar a maior distância possível, tanto na horizontal como na vertical, a curva descrita pelo objeto é aproximadamente uma parábola.

6. Chama-se função quadrática, ou função polinomial do 2º grau, qualquer função f de IR em IR dada por uma lei da forma f(x) = ax 2 + bx + c, onde a, b e c são números reais e a 0. Vejamos alguns exemplos de função quadráticas: f(x) = 3x2 - 4x + 1, onde a = 3, b = - 4 e c = 1 f(x) = x2 -1, onde a = 1, b = 0 e c = -1 f(x) = 2x2 + 3x + 5, onde a = 2, b = 3 e c = 5 f(x) = - x2 + 8x, onde a = 1, b = 8 e c = 0 f(x) = -4x2, onde a = - 4, b = 0 e c = 0

7. Os pontos de interseção com o eixo Ox (se existirem) Para resolvê-la, utilizamos a fórmula de Bhaskara : em que, Se > 0 , temos duas reízes reais distintas. Se < 0 , não temos raízes reais. Se = 0 , temos duas raízes reais e iguais. x = 2

8. > 0 a > 0 a < 0 = 0 a > 0 a < 0 < 0 a > 0 a < 0

9. Denominam-se zeros ou raízes de uma função de 2° grau os valores de x que anulam a função, ou seja, que tornam f(x)=0 As raízes da função nada mais é onde a parábola corta no eixo do x.

10. Vértice da parábola V (Xv, Yv) Xv = Yv =

12. O domínio da função é IR (real). D= IR O conjunto imagem da função é aquele formado pelas ordenadas de todos os pontos do gráfico. Essas ordenadas são todos os números reais do Y do vértice. Im= {y Є IR / y ≥ }

13. Mínimo : Se a > 0, y v = é o valor mínimo da função Im= {y Є IR / y ≥ }

14. Máximo: Se a < 0, y v = é o valor máximo da função Im= {y Є IR / y ≤ }

15. Para se estudar o sinal da função do 2º grau deve-se adotar o procedimento: Determinam-se as raízes da função. Marcam-se as raízes em uma reta (caso existam). Analisa-se a concavidade da parábola. Faz-se o estudo do sinal.

16. EXEMPLO : Estudar o sinal da função f(x)= x 2 - 5x + 6. x 2 - 5x + 6 = 0 (determina-se a raiz da função) (marcam-se as raízes em uma reta e analisa-se a concavidade da parábola) (faz-se o estudo do sinal) f(x) > 0, para x<2 ou x>3 f(x)=0, para x=2 ou x=3 f(x) < 0, para 2 < x < 3

17. O gráfico de uma função polinomial do 2º grau, y = ax 2 + bx + c, com a 0, é uma curva chamada parábola.

18. O gráfico das Funções Quadráticas: O gráfico de uma função quadrática, f (x) =ax 2 +bx+c, com a diferente de 0, é uma curva chamada parábola. Ao construir um gráfico de uma função quadrática f (x) =ax 2 +bx+c, notaremos sempre que: a>0, a parábola tem a concavidade voltada para cima (U) a<0, a parábola tem a concavidade voltada para baixo

19. Vamos construir o gráfico da função y = x 2 + x: Primeiro atribuímos a x alguns valores, depois calculamos o valor correspondente de y e, em seguida, ligamos os pontos assim obtidos.

22. Exercícios: Dada a função f(x) = 3x 2 -7x + 2, determine: Os zeros da função. O vértice da parábola. Desenhe o gráfico. O Domínio e Imagem. O valor de máximo e de mínimo. Estude o sinal da função.