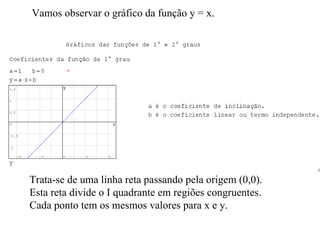
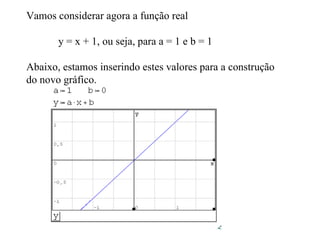
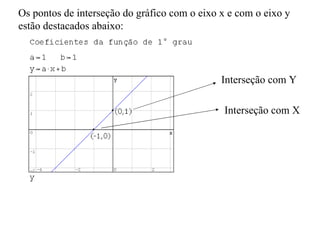
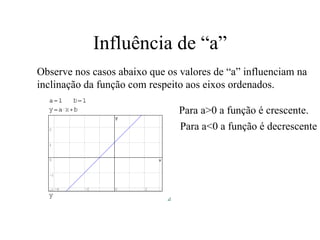
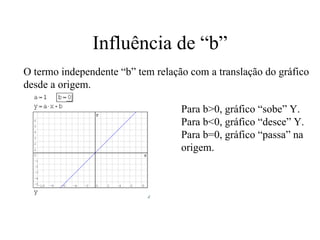
Este documento descreve as funções de 1° grau, suas características e como representá-las graficamente. Explica que uma função de 1° grau tem a forma y=ax+b, e descreve como os coeficientes a e b influenciam a inclinação e posição do gráfico. Também mostra como calcular os pontos de interseção com os eixos x e y e traça um gráfico de exemplo passo a passo.

1. Gráficos da função de 1° grau

2. Função de 1° grau É uma função real do tipo y = ax +b, ou seja: f: R R , tal que y = ax + b O coeficiente “a” é o coeficiente de inclinação. A constante “b” é o termo independente da função. A letra “x” é a variável independente. A letra “y” é a variável dependente.

3. Relação entre y e x Os valores de y dependem dos valores de x e os números que estas variáveis podem assumir são números reais. Em outras palavras, os valores de y estarão num eixo real e os valores de x estarão num outro eixo real. É por isto que se faz uso de um plano cartesiano para se repre- sentar geometricamente a relação entre y e x.

4. Vamos avaliar um exemplo. Consideremos a função real y = x (neste caso: a = 1 e b = 0) Observe a tabela abaixo de valores escolhidos para x para os valores calculados de y: Coordenadas associadas (-1,-1) (0,0) (1,1) (x,y) x – abscissa y – ordenada 1 1 0 0 -1 y = x -1 x

5. Vamos observar o gráfico da função y = x. Trata-se de uma linha reta passando pela origem (0,0). Esta reta divide o I quadrante em regiões congruentes. Cada ponto tem os mesmos valores para x e y.

6. Vamos considerar agora a função real y = x + 1, ou seja, para a = 1 e b = 1 Abaixo, estamos inserindo estes valores para a construção do novo gráfico.

7. Os pontos de interseção do gráfico com o eixo x e com o eixo y estão destacados abaixo: Interseção com Y Interseção com X

8. Quando você não usa um programa de computador, como fizemos aqui, o gráfico construído num papel quadriculado pode ser feito da seguinte forma: Trace os eixos Y e X no quadriculado. Calcule os pontos de interseção. O cálculo dos pontos de interseção é feito da seguinte forma: Para se calcular a interseção do gráfico com o eixo Y, considera-se x = 0 e determina-se y. Para se calcular a interseção do gráfico como eixo X, considera-se y = 0 e determina-se x.

9. Calculo dos pontos de interseção

11. Influência de “a” Observe nos casos abaixo que os valores de “a” influenciam na inclinação da função com respeito aos eixos ordenados. Para a>0 a função é crescente. Para a<0 a função é decrescente

12. Influência de “b” O termo independente “b” tem relação com a translação do gráfico desde a origem. Para b>0, gráfico “sobe” Y. Para b<0, gráfico “desce” Y. Para b=0, gráfico “passa” na origem.

13. Créditos finais Júnior ideia José Ximbika produção Prof. Manuel consultoria