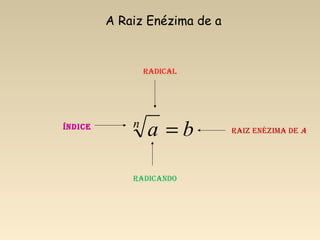
O documento discute os conceitos fundamentais de radiciação, incluindo: 1) A radiciação é a operação inversa da potenciação e envolve a extração da raiz de um número. 2) Um radical é composto pelo radicando, índice e raiz. 3) As propriedades da radiciação incluem operações com radicais como adição, subtração, multiplicação e divisão.

1. Ângelo Moreira
Radiciação

2. Na raiz , temos: = b
A radiciação é a operação inversa da potenciação.
Ex.
42pois24 2
==
n
a
RADICAL
O número n é chamado índice;
O número a é chamado radicando;
O número b é chamado raiz.

3. 3
RadiciaçãoRadiciação
Raiz quadrada de um número positivo “a” é o
número positivo que elevado ao quadrado dê “a”.
Exemplos:Exemplos:
9 3= 49 7= 81 9=
1 1= 0 0= 1,21 1,1= 6,25 2,5=
1 1
4 2
= 0,04 0,2=
636 =
5
3
25
9
=

4. ban
=
Radical
Radicando
Índice Raiz enézima de a
A Raiz Enézima de a

5. Propriedades daPropriedades da
RadiciaçãoRadiciação
( )
aae)
aad)
aac)
0)(b
b
a
b
a
b)
abbaa)
pn pmn m
nmn m
n mm
n
n
n
n
nnn
=
=
=
≠=
=⋅

6. Propriedades dos
radicais:
nnn
babaa ⋅=⋅)
Se :,,,,, temosNpNnZmRbRa ++
++ ∈∈∈∈∈
pn pmn m
aab
⋅ ⋅
=)
)0() ≠= b
b
a
b
a
c n
n
n
( ) n mm
n
aad =)
npp n
aae
⋅
=)
3333
102525 =⋅=⋅
6 423 2.23 2
555 == ⋅
4
4
4
3
5
3
5
=
( ) ( ) 322288 5
5
3 35
33 5
====




 6233
777 == ⋅

7. Radicais SemelhantesRadicais Semelhantes
Dois ou mais radicais são semelhantes,Dois ou mais radicais são semelhantes,
quando possuem o mesmo índice e mesmoquando possuem o mesmo índice e mesmo
radicandoradicando
32 37
3
54− 3
56−
e
e

8. RADICIAÇÃO
Potência com expoente racional
Observe as seguintes igualdades:
ou
Igualmente podemos transformar uma potência com expoente fracionário em um
radical.
De modo geral, definimos:
, com a IR,m,n, IN, a >0, n>0, m>0
Podemos também transformar um radical com expoente fracionário, isto é,vale
também a volta.
Veja mais um exemplo:
60 13260 13360
133
5
4
4
3
3
2
5
4
4
3
3
2
5 44 33 2
..... aaaaaaaaaaa =====






++

9. RADICIAÇÃO
Potência com expoente racional
Propriedade das potências com expoentes racionais
As propriedades das potências com expoentes racionais são as mesmas para
os expoentes inteiros.
Sendo a e b números reais e positivos e os expoentes números racionais,
temos que:
( )
n
m
n
m
n
m
n
m
n
m
n
m
q
p
n
m
q
p
n
m
q
p
n
m
q
p
n
m
b
a
b
a
baba
a
a
a
aaa
=





=
=
=
−
+
..
.

10. SimplificandoSimplificando
RadicaisRadicais
23632233223
32233232883b)
22228a)
224
2425
236 336 36
=⋅⋅⋅=⋅⋅⋅
=⋅⋅=⋅=
==== ÷ ÷
Simplificar um radical é reduzir o radicando à sua expressão
mais simples.
Exemplos:

11. RADICIAÇÃO
“Introdução” de um fator no radical
 33 333 33
567.27.27.2 === Processo prático: 33 33
567.272 ==
44 44
300003.10310 ==
1805.656 2
==
5005.10510 2
==

12. RADICIAÇÃO
Operações com Radicais:
Adição e Subtração
Exemplo 1: Efetue:
Resolução: Os três radicais são semelhantes, pois possuem o mesmo índice 2 e
o mesmo radicando 3. Adicionando algebricamente os coeficientes, podemos
escrever:
37333 −+
( ) 32731337333 −=−+=−+
Exemplo 2: Efetue:
Resolução: Os três radicais aparentemente não são semelhantes, mas se os
simplificarmos, perceberemos que eles são verdadeiramente semelhantes.
Simplificando cada um dos radicais, teremos:
1843283 +−
214212242623.42222.33.242223 2253
=+−=+−+−

13. RADICIAÇÃO
Operações com Radicais:
Adição e Subtração
Exemplo 3: Efetue:
Resolução: Os três radicais aparentemente não são semelhantes, mas se os
simplificarmos, perceberemos que eles são semelhantes dois a dois.
Simplificando cada um dos radicais, teremos:
864
8112540075 +−+
536355.235355.25.3 28 46 34 242
+=+−+=+−+

14. RADICIAÇÃO
Operações com Radicais:
Multiplicação
Exemplo 1: 5.2
Resolução: Os dois são homogêneos, pois possuem o mesmo índice 2. Multiplicando os
radicandos e conservando o índice, podemos escrever: 105.25.2 ==
Exemplo 2: Efetue: 5 44 33 2
.. aaa
Resolução: Os três radicais são heterogêneos, pois possuem índices diferentes. Reduzindo-os
ao mesmo índice, teremos: 60 13360 48454060 4860 4560 405 44 33 2
...... aaaaaaaaaa ===
E simplificando o radical teremos:60 133
a
60 13260 13120
.. aaaa =

15. RADICIAÇÃO
Operações com Radicais:
Divisão

16. RADICIAÇÃO
Operações com Radicais:
Divisão

17. RADICIAÇÃO
Operações com Radicais:
Potenciação
( ) 55 35555
3
5
822.2.22.2.22 ====
Logo, ( ) 1.35 3
3
5 1
.22 ←
=
( ) 7 67 337 37 3
2
7 3
55.55.55 ===
Logo,
( ) 3.27 6
2
7 3
.55 ←
=
( ) n mr
m
n r
aa =
De modo geral, para se elevar um radical a um dado expoente, basta elevar
o radicando àquele expoente.

18. Radiciação
RADICIAÇÃO
2642864 633
=== e Logo, 63 2
6464 =
2.3
3813981 4
=== e Logo, 42 2
8181 =
2.2
28644096 333
===
2240964096 12 12123
===
ou
De modo geral, satisfeitas as condições de existência dos radicais
envolvidos, podemos indicar a radiciação de um radical assim:
nmn m
aa .
=
Operações com Radicais:

19. Expressões
RADICIAÇÃO
=−+=+−+=+−+ 333
984185484182548418
327918811838418 3333
==+=+=−+=

 =+=
−
+=−+ 333
25
4
125
14
25
1115
125
14
25
11
5
3
125
14
5
4
125
64
125
5014
5
2
125
14 333 ==
+
=+=
 246416.416.13:5216.13:52 333333
=====

2
1
3.7.2
3.7
3.7.2
3.23.5
7.3.2
3.25.3
588
1275
22
22
==
+
=
+
=
+

20. RADICIAÇÃO
Desenvolvendo Produtos Notáveis
( ) ( )( ) ( ) 246224422222422.2222
22
+=++=++=++=+
 ( )( ) ( ) ( ) 36366.36.3363.63
22
−=−=+−+=+−
( ) ( )( ) ( ) ( ) ( ) ( ) 30.213330.21033.103.1010310.310310
222
−=+−=+−−=−−=−

21. RADICIAÇÃO
Racionalização de Denominadores
Em alguns cálculos, você pode se deparar com raízes no denominador da
fração, o que a torna irracional. Para que você possa prosseguir com os
cálculos, é conveniente que você elimine essas raízes do denominador, esse
processo chamado de racionalização de denominadores. Isto é, transforma-se
um denominador irracional em racional, para que assim possamos trabalhar
com tranquilidade com a fração que agora teremos
o denominador é um número irracional e deve ser eliminado.
Atenção: o importante é eliminar a raiz (que pode ser quadrada, cúbica, etc),
mantendo uma fração "equivalente", ou seja, que representa o mesmo valor.
Uma dica é multiplicar tanto o numerador (parte de cima), quanto o denominador
pelo mesmo número, o que não interfere na igualdade. Se a fração anterior for
multiplicada em cima e em baixo por ficará:
Note que é igual a 1, logo a multiplicação de um número por 1 não o altera.

22. RADICIAÇÃO
Racionalização de Denominadores
Prosseguindo:
Como se pode notar o denominador agora é um número racional (3).

23. RADICIAÇÃO
Racionalização de Denominadores
Raízes não-quadradas
Para eliminar raízes cúbicas, ou de outros índices diferentes de 2 (lembre-se: raiz
quadrada é, na verdade, uma raiz de índice 2), é necessário utilizar um artifício.
Multiplique, no numerador e no denominador, por uma raiz de mesmo radicando (o
número dentro da raiz) e cujo índice seja equivalente ao índice da raiz original, e o
expoente do radicando seja o valor do índice menos um. Por exemplo:
é o fator racionalizante de
ou

24. RADICIAÇÃO
Racionalização de Denominadores
Soma de raízes no denominador
Veja:
Deve-se multiplicar por
Isso porque a multiplicação de por é, na verdade, a multiplicação de
(a + b). (a - b), um produto notável, cujo resultado é (a2
- b2
), isto é, os radicais
somem!
é o fator racionalizante de
é o fator racionalizante de
é o fator racionalizante de