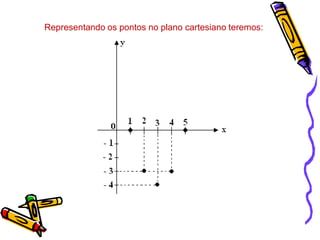
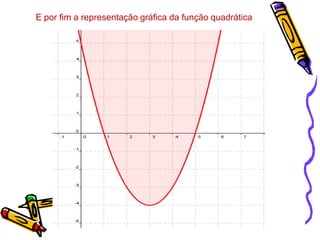
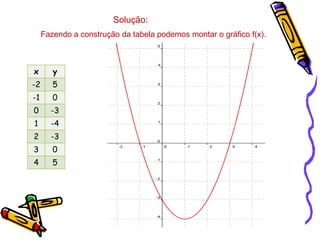
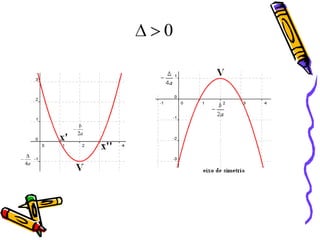
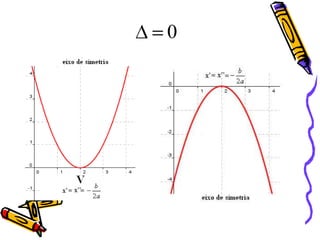
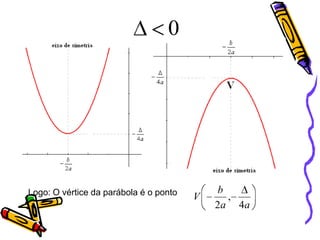
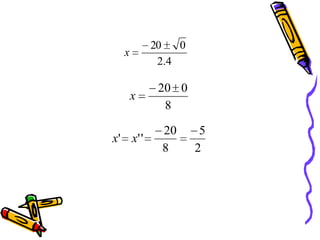O documento descreve as funções quadráticas ou funções do segundo grau, definindo-as como funções da forma f(x)=ax2+bx+c. Explica como calcular os valores de a, b e c a partir de pontos dados e como representar graficamente essas funções, incluindo a localização do vértice e dos zeros.

1. FUNÇÃO DO 2º GRAU
OU
FUNÇÃO QUADRÁTICA

2. DEFINIÇÃO:
A função f: IR em IR dada por
f(x) = ax² + bx + c, com a, b, c
reais e a ≠ 0, denomina-se
função quadrática ou função
do 2º grau.

3. São exemplos de função de função do 2º grau:
f(x) = x² - 4x – 3, onde a = 1, b = - 4 e c = - 3
f(x) = x² - 9, onde a = 1, b = 0 e c = - 9
f(x) = 6x², onde a = 6, b = 0 e c = 0
f(x) = - 4x² + 2x, onde a = - 4, b = 2 e c = 0

4. Ex.: Considere a função do 2º grau f(x) = ax² + bx + c. Sabendo que
f(0) = 5, f(1) = 3 e f(- 1) = 1, calcule os valores de a, b e c e escreva
a função f.
Solução:
Inicialmente iremos substituir o valor de x e f(x) na
função f(x) = ax² + bx + c. Assim:
f(0) = a.0² + b.0 + c, como f(0) = 5 vem que:
C=5
f(1) = a.1² + b.1 + c
a + b + c = 3, substituindo o valor de c fica:
a+b+5=3
a+b=-2
f(- 1) = a.(- 1)² + b(- 1) + c
a–b+c=1
a–b+5=1
a–b=-4

5. a b
Resolvendo o sistema:
a b
2
4
a
b
2
a
b
4
2a
a
a
6
6
2
3

6. Substituindo o valor de a em uma das equações teremos:
a b
2
3 b
b
2
2 3
b 1
Portanto os valores de a = - 3, b = 1 e c = 5. A função tem sua
representação algébrica f(x) = - 3x² + x + 5

7. GRÁFICO DA FUNÇÃO
DO 2º GRAU

8. Para construir o gráfico de uma função
quadrática ou do 2º grau no plano
cartesiano, vamos proceder da
seguinte maneira:
1.Atribuindo valores a x;
2.Representando os pontos no plano
cartesiano;
3.Ligando os pontos de variável real.

9. Ex.: represente no plano cartesiano a função real
f(x) = x² - 6x + 5.
Solução:
Construindo uma tabela com valores arbitrários para x vem
x
f(x) = x² - 6x + 5
(x, y)
1
f(1) = 1² - 6.1 + 5 = 1 – 6 + 5 = - 5 + 5 = 0
(1, 0)
2
f(2) = 2² - 6.2 + 5 = 4 – 12 + 5 = - 8 + 5 = - 3
(2, - 3)
3
f(3) = 3² - 6.3 + 5 = 9 – 18 + 5 = -9 + 5 = - 4
(3, - 4)
4
f(4) = 4² - 6.4 + 5 = 16 – 24 + 5 = - 8 + 5 = - 3
(4, - 3)
5
f(5) = 5² - 6.5 + 5 = 25 – 30 + 5 = - 5 + 5 = 0
(5, 0)

10. Representando os pontos no plano cartesiano teremos:

11. E por fim a representação gráfica da função quadrática

12. ZEROS DE UMA FUNÇÃO QUADRÁTICA
Denomina-se zeros ou raízes de uma função quadrática os
valores de x que anulam a função, ou seja, que tornam f(x) = 0.
•Se ∆ > 0, a função tem dois zeros reais e distintos (x’ ≠ x’’)
•Se ∆ = 0, a função apresenta tem dois zeros iguais (x’ = x’’)
•Se ∆ < 0, a função não tem zero real

13. Ex.: Vamos encontrar, se existir, os zeros da
função f(x) = x² - 4x – 5.
Solução:
x² 4 x 5 0
b² 4ac
( 4)² 4.1.( 5)
16 20 36 0
Como ∆ > 0 a função tem dois zeros reais. Assim:
x
b
2a
Calculemos agora seus zeros:

14. x
x
4 6
2
( 4)
36
2 .1
4 6 10
x'
5
2
2
4 6
2
x' '
1
2
2
Logo, os zeros da função são – 1 e 5

15. Ex.: Determinar os zeros da função y = x² - 2x + 6.
Solução:
( 2)² 4.1.6
4 24
20 0
Como ∆ < 0, a função não tem zero real
Ex.: Determinar os zeros da função y = 4x² + 20x + 25.
Solução:
(20)² 4.4.25 400 400 0
Como ∆ = 0 a função tem dois zeros reais e iguais.
Continuemos então a resolução:

16. 20
0
2.4
x
x
x' x' '
20 0
8
20
8
5
2

17. INTERPRETAÇÃO GRÁFICA DOS ZEROS DE UMA FUNÇÃO
QUADRÁTICA
Pela definição dada anteriormente, vimos que os zeros ou
raízes da função f(x) = ax² + bx + c sâo os valores de x para os
quais f(x) = 0
Ex.: Construir o gráfico da função f(x) = x² - 2x – 3.

18. Solução:
Fazendo a construção da tabela podemos montar o gráfico f(x).
x
y
-2
5
-1
0
0
-3
1
-4
2
-3
3
0
4
5

19. Note que a função intercepta o eixo das abscissas em dois pontos
distintos, ou seja, para esses dois valores f(x) = 0.
Portanto temos os zeros da função quadrática.

20. ESTUDO DO VÉRTICE DA PARÁBOLA
A parábola, que representa o gráfico da função f(x) = ax² + bx
+ c, passa por um ponto V, chamado vértice, cujas coordenadas são:
xv
b
(abscissa )
2a
yv
4a
(ordenada)
Os esboços dos gráficos, nos diversos casos são os seguintes:

21. 0
b
2a
4a

22. 0

23. 0
Logo: O vértice da parábola é o ponto
V
b
,
2a 4a

24. O pensamento é muito
mais importante do que o
conhecimento “Albert
Heinstein”