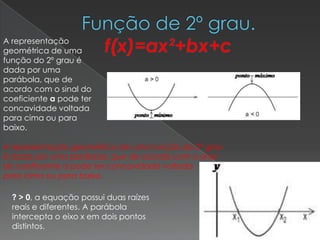
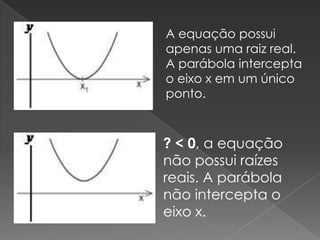
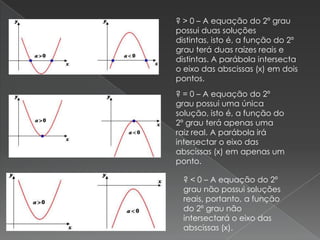
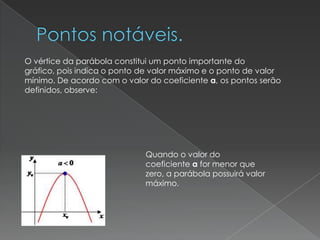
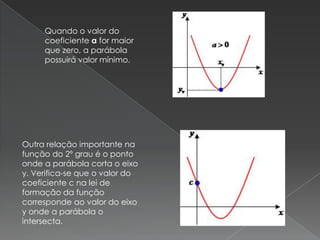
O documento discute funções do 1o e 2o grau. Apresenta um exemplo de função do 1o grau f(x)=x-2 e explica como encontrar seus pares ordenados (x, f(x)). Também explica que a representação geométrica de uma função do 2o grau é dada por uma parábola e como seus coeficientes determinam se a parábola corta o eixo x em um, dois ou nenhum ponto.

2.  Note que para definir a função do 1°
grau, basta haver uma expressão
algébrica do 1° grau. Como dito
anteriormente, o objetivo da função é
relacionar para cada valor de x um
valor para o f(x).

3.  Vejamos um exemplo para a função f(x)= x
– 2.
a) x = 1, temos que f(1) = 1 – 2 = –1
b) x = 4, temos que f(4) = 4 – 2 = 2
 Note que os valores numéricos mudam
conforme o valor de x é alterado, sendo
assim obtemos diversos pares
ordenados, constituídos da seguinte
maneira: (x, f(x)). Veja que para cada
coordenada x, iremos obter uma
coordenada f(x). Isso auxilia na construção
de gráficos das funções.

4. y
a) b) Sua vez de fazer o
3
gráfico, é a mesma
coisa, mas com
2
-3 -2 -1 1 2 3 4 outros números.
x
-1
-2
-3
X= -1 Y= -1

5. A representação
geométrica de uma
função do 2º grau é
dada por uma
parábola, que de
acordo com o sinal do
coeficiente a pode ter
concavidade voltada
para cima ou para
baixo.
A representação geométrica de uma função do 2º grau
é dada por uma parábola, que de acordo com o sinal
do coeficiente a pode ter concavidade voltada
para cima ou para baixo.
? > 0, a equação possui duas raízes
reais e diferentes. A parábola
intercepta o eixo x em dois pontos
distintos.

6. A equação possui
apenas uma raiz real.
A parábola intercepta
o eixo x em um único
ponto.
? < 0, a equação
não possui raízes
reais. A parábola
não intercepta o
eixo x.

7. ? > 0 – A equação do 2º grau
possui duas soluções
distintas, isto é, a função do 2º
grau terá duas raízes reais e
distintas. A parábola intersecta
o eixo das abscissas (x) em dois
pontos.
? = 0 – A equação do 2º
grau possui uma única
solução, isto é, a função do
2º grau terá apenas uma
raiz real. A parábola irá
intersectar o eixo das
abscissas (x) em apenas um
ponto.
? < 0 – A equação do 2º
grau não possui soluções
reais, portanto, a função
do 2º grau não
intersectará o eixo das
abscissas (x).

8. O vértice da parábola constitui um ponto importante do
gráfico, pois indica o ponto de valor máximo e o ponto de valor
mínimo. De acordo com o valor do coeficiente a, os pontos serão
definidos, observe:
Quando o valor do
coeficiente a for menor que
zero, a parábola possuirá valor
máximo.

9. Quando o valor do
coeficiente a for maior
que zero, a parábola
possuirá valor mínimo.
Outra relação importante na
função do 2º grau é o ponto
onde a parábola corta o eixo
y. Verifica-se que o valor do
coeficiente c na lei de
formação da função
corresponde ao valor do eixo
y onde a parábola o
intersecta.

10. Determine os pontos de intersecção da parábola da função f(x) =
2x² – 3x + 1, com o eixo das abscissas.
RESPOSTA: No instante em que a parábola cruza o eixo das
abscissas o valo de y ou f(x) é igual a zero. Portanto:
f(x) = 0
2x² – 3x + 1 = 0
Então: Os pontos de interseção são:
x=1ey=0
x = 1/2 e y = 0
Feito por : Gustavo