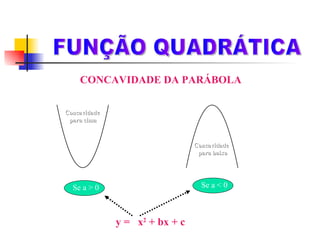
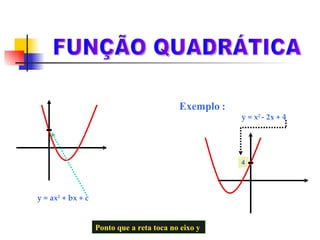
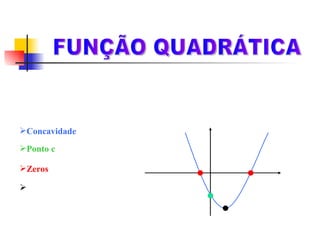
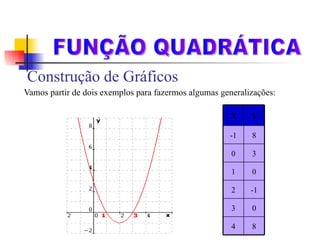
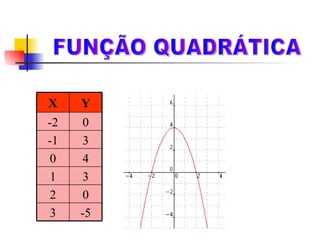
Este documento discute funções quadráticas e como elas podem ser usadas para modelar o movimento de uma bola chutada por um goleiro. A função h = 20t - 5t2 é usada para descrever a altura da bola em relação ao tempo. O documento também define funções quadráticas, discute suas propriedades como concavidade e vértice, e mostra como construir gráficos de funções quadráticas.

1. FUNÇÃO QUADRÁTICA DEFINIÇÃO CONCAVIDADE DA PARÁBOLA ZEROS DA FUNÇÃO TERMO INDEPENDENTE ESBOÇO DO GRÁFICO VÉRTICE

2. Introdução Vamos analisar o movimento de uma bola após ser chutada por um goleiro, em um tiro de meta (velocidade inicial de 72 km/h). FUNÇÃO QUADRÁTICA

3. A altura da bola varia em função do tempo. Veja a tabela a seguir. FUNÇÃO QUADRÁTICA 4 0 3 15 2 20 1 15 TEMPO (s) ALTURA (m)

4. Note que, claramente, a bola ganha altura até 2 segundos e depois perde altura, chegando ao chão novamente no instante 4 segundos. A função que fornece a altura, neste caso, em função do tempo é dada por: h = 20t – 5t 2 FUNÇÃO QUADRÁTICA

5. Provavelmente, Galileu foi o primeiro a observar que um objeto em queda livre percorre distâncias proporcionais ao quadrado do tempo decorrido. FUNÇÃO QUADRÁTICA 45 3 20 2 5 1 h (m) t (s)

6. DEFINIÇÃO FUNÇÃO QUADRÁTICA Seja f : IR – IR uma função definida por y = ax 2 + bx + c Dizemos que f é uma Função Quadrática , onde a , b e c são constantes reais e “ x ” é a variável em questão. O gráfico descrito por uma função quadrática é uma Parábola

7. FUNÇÃO QUADRÁTICA Identificação de coeficientes da função quadrática 2x 2 - 3x + 5 = 0 a = 2 b =-3 c = 5 -x 2 + 4x - 3 = 0 a =-1 b = 4 c = -3 4x + 8x 2 - 4 = 0 a = 8 b = 4 c = -4 3x - 6x 2 = 0 a = -6 b = 4 c = -4

8. FUNÇÃO QUADRÁTICA CONCAVIDADE DA PARÁBOLA Concavidade para cima Concavidade para baixo y = a x 2 + bx + c Se a > 0 Se a < 0

9. TERMO INDEPENDENTE FUNÇÃO QUADRÁTICA c y x y = ax 2 + bx + c Exemplo : 4 y x y = x 2 - 2x + 4 Ponto que a reta toca no eixo y

10. FUNÇÃO QUADRÁTICA ESBOÇO DO GRÁFICO Para construir um gráfico de uma função quadrática devemos ter : Concavidade Ponto c Zeros Vértice y x

11. FUNÇÃO QUADRÁTICA Zeros ou Raízes Já sabemos que os zeros (ou as raízes) de uma função são os valores de x que fazem y = 0. No caso de uma função quadrática, teremos uma equação do segundo grau. Relembremos então a técnica estudada.

12. Construção de Gráficos Vamos partir de dois exemplos para fazermos algumas generalizações: FUNÇÃO QUADRÁTICA Exemplo 1 : y = f(x) = x² - 4x + 3 0 3 8 4 -1 2 0 1 3 0 8 -1 Y X

13. FUNÇÃO QUADRÁTICA Exemplo 2 : y = f(x) = -x² + 4 0 2 -5 3 3 1 4 0 3 -1 0 -2 Y X

14. Coordenadas do Vértice y = ax 2 + bx + c FUNÇÃO QUADRÁTICA Ponto mínimo Ponto máximo Em qualquer caso, as coordenadas do vértice são dadas por:

15. Coordenadas do Vértice FUNÇÃO QUADRÁTICA

16. Comentários Finais O estudo das funções quadráticas é muito importante para a Física e para a Engenharia, pois descreve o movimento dos corpos sob ação da gravidade.

17. Componente: Samuel Messias Vitor