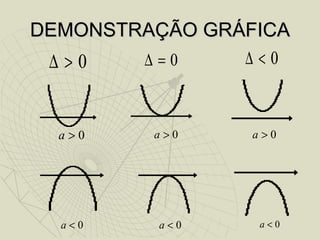
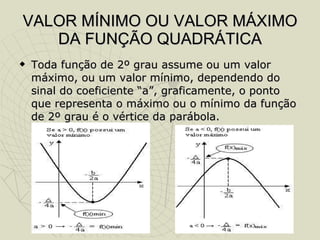
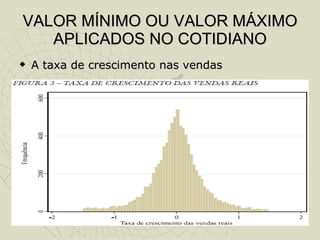
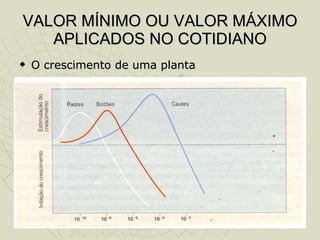
O documento discute a origem e fundamentos da função quadrática. Resume que as funções quadráticas surgiram originalmente das equações de segundo grau, desenvolvidas por Euclides em 300 a.C. Explica que as funções quadráticas têm como gráfico a parábola e definem-se como f(x)=ax2+bx+c. Discutem a representação gráfica, raízes, vértice e valores máximo e mínimo das funções quadráticas e apresentam exemplos de sua aplicação no cotidiano.

1. ORIGEM E FUNDAMENTOS DA FUNÇÃO QUADRÁTICA Tarefa Individual Final Informática Educativa II :: Objeto de Aprendizagem Aluna: Luciane Antoniolli

2. A ORIGEM A noção de função do 2º grau ou função quadrática associa-se originalmente à ideia de equação do 2º grau, por volta de 300 a.C., o matemático grego Euclides ( 325-265 a.C) desenvolveu uma nova técnica denominada Álgebra Geométrica. No Renascimento destacou-se as tentativas de explicar o movimento de queda livre de um corpo ou trajetória de uma bola de canhão, que é uma parábola, vários teóricos dos séculos XVI e XVII tentaram explicar essa trajetória, sem obter a parábola, tais explicações foram aperfeiçoadas até se chegar à parábola associada à curva de 2º grau, o que acelerou a necessidade de se relacionar curvas a equações, de modo geral, álgebra à geometria.

3. DEFINIÇÃO Em geral, uma função quadrática ou polinomial do segundo grau é expressa da seguinte forma: f (x) =ax²+bx+c, sendo a≠0 As funções de segundo grau têm a variável independente com grau 2, ou seja, o seu maior expoente é 2. O gráfico que corresponde a essas funções é uma curva denominada parábola.

4. REPRESENTAÇÃO GRÁFICA DA FUNÇÃO QUADRÁTICA Sua representação gráfica é dada em torno de eixos:

5. VALOR DO COEFICIENTE “a” De acordo com o valor do coeficiente “a”, a parábola assume concavidade voltada para cima ou para baixo. Exemplos: y = f(x) = x² - 4 y = f(x) = -x² + 4 a=1, a>0 a=-1, a<0

6. ZEROS ( OU RAÍZES) DE UMA FUNÇÃO QUADRÁTICA Chama-se zeros ou raízes da função polinomial do 2º grau f(x) = ax² + bx + c , a≠0, os valores de “x” que anulam a função, ou seja tornam f(x)=0, valores estes que são obtidos pela chamada fórmula de Bhaskara: Onde b²-4ac, é chamado de Discriminante e representado pela letra grega Δ (delta).

7. EXEMPLOS DE RAÍZES DA FUNÇÃO QUADRÁTICA A quantidade de raízes reais de uma função quadrática depende do valor obtido para o radicando Δ =b²-4ac. Se Δ >0, a função tem dois zeros reais desiguais (x’ e x”); Se Δ =0, a função tem um zero real duplo (x’=x”); Se Δ <0, a função não tem zero real.

8. DEMONSTRAÇÃO GRÁFICA

9. AS PARÁBOLAS NO COTIDIANO Temos alguns exemplos de construções com parábolas

10. VÉRTICE DA PARÁBOLA A parábola, que representa o gráfico da função f(x)=ax²+bx+c, passa por um ponto V, chamado vértice. Coordenada “ Xv” do vértice: Fica exatamente no meio das coordenadas das duas raízes, onde a coordenada &quot;x&quot; do vértice é a média aritmética das coordenadas &quot;x&quot; das raízes, isto é, a soma das duas dividido por dois: Exemplo:

11. VÉRTICE DA PARÁBOLA Coordenada “ Yv” do vértice : Para encontramos a coordenada Yv , basta substituirmos o valor encontrado para Xv, no lugar do x da função, e encontraremos o o F(Xv), ou apenas o Yv. Exemplo:

12. VÉRTICE DA PARÁBOLA Através do estudo anterior sobre o vértice da parábola, obtivemos as seguintes fórmulas: a>0, o V é Ponto de Mínimo de f; a<0, o V é Ponto de Máximo de f.

13. VALOR MÍNIMO OU VALOR MÁXIMO DA FUNÇÃO QUADRÁTICA Toda função de 2º grau assume ou um valor máximo, ou um valor mínimo, dependendo do sinal do coeficiente “a”, graficamente, o ponto que representa o máximo ou o mínimo da função de 2º grau é o vértice da parábola.

14. A UTILIZAÇÃO DOS VALORES MÍNIMO E MÁXIMO NO COTIDIANO O valores máximo e mínimo de uma função quadrática podem ser analisados em muitas situações cotidianas em que temos a aplicação de uma parábola, a palavra parábola provém do grego e significa “lançar ao longe”, o seu significado foi sempre muito associado a trajetória de um objeto lançado sob determinado ângulo. Atribuímos também a parábola e os pontos de máximo e de mínimo a situações que envolvam lucro, prejuízo, crescimento, potência e a outras análises presentes na Física, Biologia, Administração, Contabilidade, entre outras ciências.

15. VALOR MÍNIMO OU VALOR MÁXIMO APLICADOS NO COTIDIANO O lançamento de uma bola

16. VALOR MÍNIMO OU VALOR MÁXIMO APLICADOS NO COTIDIANO A altura máxima alcançada pela nuvem de partículas após uma implosão

17. VALOR MÍNIMO OU VALOR MÁXIMO APLICADOS NO COTIDIANO A taxa de crescimento nas vendas

18. VALOR MÍNIMO OU VALOR MÁXIMO APLICADOS NO COTIDIANO O crescimento de uma planta

19. Conclusão Tudo que foi apresentado neste trabalho nos faz analisar que os fundamentos matemáticos tem uma profunda relação com o cotidiano de todos nós, esteja ele relacionado com a educação, com o trabalho, ou até mesmo com os momentos de lazer, e analisando a função quadrática comprovamos que ela está muito mais presente em nossas vidas do que imaginamos, pois quando estudamos os valores mínimo e máximo desta função, vimos que ela tem uma profunda relação com o ser humano e também com a natureza, seja no cálculo do crescimento de uma planta, ou na área financeira, mas o fundamental neste estudo das funções quadráticas, é que possamos demonstrá-la com exemplos que torne o aprendizado muito mais significativo para todos. “ A Matemática é o alfabeto com o qual Deus escreveu o universo.” (Galileu Galilei)

20. REFERÊNCIAS BIBLIOGRÁFICAS PAIVA, Manoel. Matemática: Conceitos, linguagem e aplicações. São Paulo: Moderna, 2002. v.1. DANTE, Luiz Roberto. Matemática: contexto e aplicações. Vol. 1, 2 e 3. Editora Ática, 2003. GIOVANNI e BONJORNO. Matemática Fundamental: uma nova abordagem. Volume único. Editora FTD, 2002. BIEMBENGUT, Maria Salett. Modelagem Matemática e Implicação no Ensino e Aprendizagem de Matemática. Blumenau: FURB, 1999.