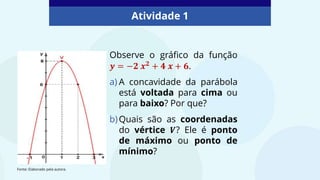
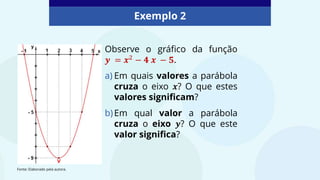
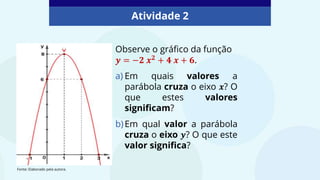
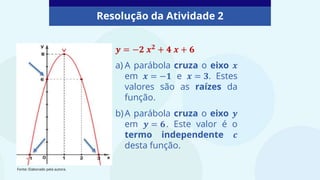
O documento aborda funções polinomiais do 2º grau, conhecidas como funções quadráticas, representadas por f(x) = ax² + bx + c, onde a ≠ 0. Explora as características da parábola, incluindo concavidade e o vértice, além de exemplificar a interseção com os eixos x e y. Atividades práticas são fornecidas para a identificação de raízes e termos independentes das funções apresentadas.

2. 3º Termo do Ensino Médio da EJA
Parte III
Funções Polinomiais do 2º Grau

3. Denominamos função polinomial de 2º grau ou função
quadrática a função 𝒇 𝒙 = 𝒂 𝒙2
+ 𝒃 𝒙 + 𝒄 ou 𝒚 = 𝒂 𝒙2
+ 𝒃 𝒙 + 𝒄,
em que 𝒂, 𝒃 e 𝒄 são constantes, sendo 𝒂 ≠ 𝟎.
Função Polinomial do 2º Grau
O gráfico da função quadrática é uma parábola.
𝒚 = 𝒙2 − 𝟒 𝒙 − 𝟓
𝒇 𝒙 = 𝟑 𝒙𝟐 + 𝟐𝒙 + 𝟏
𝒈 𝒙 = −𝒙𝟐 + 𝟒
𝒉 𝒙 = −𝟔 𝒙𝟐 + 𝒙
Fonte: Elaborado pela autora.

4. A parábola que pode ter a concavidade voltada para cima ou para
baixo, dependendo do valor do coeficiente 𝒂.
Coeficiente 𝒂 e Vértice V
Fonte: Elaborado pela autora.
𝒚 = 𝒂 𝒙2
+ 𝒃 𝒙 + 𝒄
𝒂 > 𝟎 (positivo) 𝒂 < 𝟎 (negativo)
Coordenadas do Vértice ⇒ 𝑽 𝒙𝑽, 𝒚𝑽

5. Observe o gráfico da função
𝒚 = 𝒙2
− 𝟒 𝒙 − 𝟓.
a) A concavidade da parábola
está voltada para cima ou
para baixo? Por que?
b)Quais são as coordenadas
do vértice 𝑽? Ele é ponto de
máximo ou ponto de
mínimo?
Exemplo 1
Fonte: Elaborado pela autora.

6. 𝒚 = 𝒙2
− 𝟒 𝒙 − 𝟓
a) A concavidade está voltada
para cima porque 𝒂 = 𝟏
(positivo).
b)𝑽(𝟐, −𝟗), como 𝒂 = 𝟏 (positivo)
o vértice é ponto de mínimo.
Resolução do Exemplo 1
Fonte: Elaborado pela autora.

7. Observe o gráfico da função
𝒚 = −𝟐 𝒙𝟐 + 𝟒 𝒙 + 𝟔.
a) A concavidade da parábola
está voltada para cima ou
para baixo? Por que?
b)Quais são as coordenadas
do vértice 𝑽? Ele é ponto
de máximo ou ponto de
mínimo?
Atividade 1
Fonte: Elaborado pela autora.

8. 𝒚 = −𝟐 𝒙𝟐
+ 𝟒 𝒙 + 𝟔.
a) A concavidade está voltada
para baixo porque 𝒂 = −𝟐
(negativo).
b)𝑽(𝟏, 𝟖) , como 𝒂 = −𝟐
(negativo) o vértice é ponto
de máximo.
Resolução da Atividade 1
Fonte: Elaborado pela autora.

9. 𝒚 = 𝒂 𝒙2 + 𝒃 𝒙 + 𝒄
A parábola cruza o eixo 𝒙 do plano cartesiano nas
raízes da função, ou seja, nos valores de 𝒙 que
fazem o valor de 𝒚 ser igual a zero.
A parábola cruza o eixo 𝒚 do plano cartesiano no
valor do termo independente, ou seja, quando 𝒚 é
igual a 𝒄.
Raízes e Termo Independente

10. Observe o gráfico da função
𝒚 = 𝒙2 − 𝟒 𝒙 − 𝟓.
a) Em quais valores a parábola
cruza o eixo 𝒙? O que estes
valores significam?
b)Em qual valor a parábola
cruza o eixo 𝒚? O que este
valor significa?
Exemplo 2
Fonte: Elaborado pela autora.

11. 𝒚 = 𝒙2 − 𝟒 𝒙 − 𝟓
a) A parábola cruza o eixo 𝒙 em
𝒙 = −𝟏 e 𝒙 = 𝟓. Estes valores
são as raízes da função.
b)A parábola cruza o eixo 𝒚 em
𝒚 = −𝟓. Este valor é o termo
independente 𝒄 desta
função.
Resolução do Exemplo 2
Fonte: Elaborado pela autora.

12. Observe o gráfico da função
𝒚 = −𝟐 𝒙𝟐 + 𝟒 𝒙 + 𝟔.
a) Em quais valores a
parábola cruza o eixo 𝒙? O
que estes valores
significam?
b)Em qual valor a parábola
cruza o eixo 𝒚? O que este
valor significa?
Atividade 2
Fonte: Elaborado pela autora.

13. 𝒚 = −𝟐 𝒙𝟐 + 𝟒 𝒙 + 𝟔
a) A parábola cruza o eixo 𝒙
em 𝒙 = −𝟏 e 𝒙 = 𝟑. Estes
valores são as raízes da
função.
b)A parábola cruza o eixo 𝒚
em 𝒚 = 𝟔. Este valor é o
termo independente 𝒄
desta função.
Resolução da Atividade 2
Fonte: Elaborado pela autora.

14. Agradecemos sua participação!
Bons estudos!