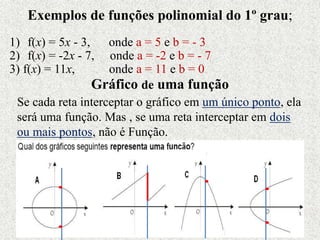
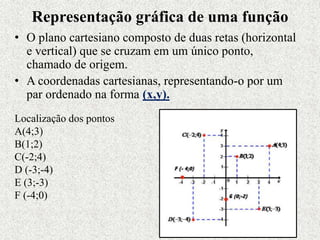
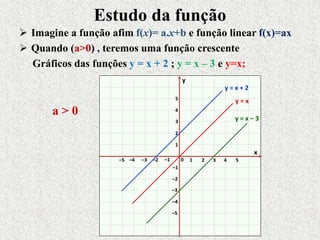
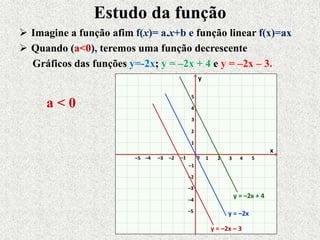
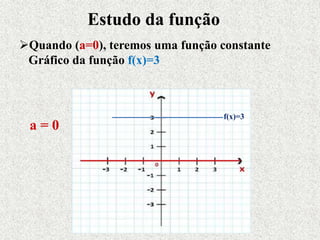
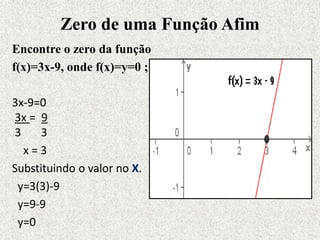
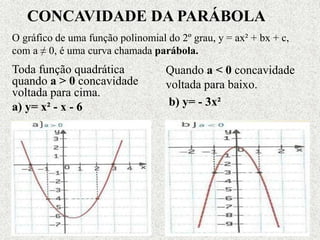
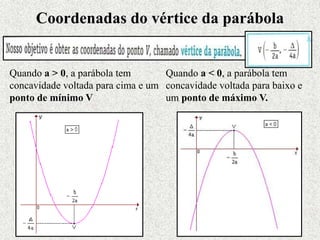
Este documento fornece um resumo sobre funções polinomiais do 1o e 2o grau. Ele define o que são funções do 1o grau e suas características, como ter um gráfico em forma de reta. Também define funções do 2o grau, cujo gráfico forma uma parábola, e explica como determinar zeros, vértice e máximos/mínimos destas funções.

1. Função Polinomial do 1º grau
Prof:Zaqueu Oliveira

2. Objetivos
• Compreender o conceito de função.
• Escrever a lei de formação de uma função
• Identificar a variável dependente e independente.
• Representar uma função por meio de gráficos.
• Classificar as funções em crescente ou
decrescente.
• Determinar o zero de uma função, o ponto de
interseção de seu gráfico.
• Determinar o ponto de máximo e mínimo.

3. História
•Desde o tempo dos Gregos até à Idade Moderna a
teoria dominante era a Geometria Euclidiana que
tinha como elementos base o ponto, a reta e o plano.
•A noção de função vai ser um dos fundamentos do
Cálculo Infinitesimal. Foi Leibniz (1646 - 1716) quem
primeiro usou o termo "função" em 1673 no
manuscrito Latino "Methodus tangentium inversa, seu
de fuctionibus".
•Um retoque final nesta definição viria a ser dado em
1748 por Euler (1707 - 1783) - um antigo aluno de
Bernoulli - substituindo o termo "quantidade" por
"expressão analítica". Foi também Euler quem
introduziu a notação f(x).

4. Algumas situações de funções
O valor da fatura de telefone
é calculado em função do
consumo no mês. F(x)= 30+C
O tempo de uma viagem está
em função da velocidade
praticada no trajeto.

5. Definição
Chama-se função polinomial do 1º grau, ou função
afim,a qualquer função de IR em IR dada por uma lei da
formação f(x)= ax+b .
1. E podemos dizer f(x) = y, logo y= ax+b
2. Onde a e b são números reais dados e a ≠ 0.
3. O gráfico dessa função é sempre uma reta.
4. A função de Primeiro Grau é a função de grau 1.

6. Exemplos de funções polinomial do 1º grau;
1) f(x) = 5x - 3, onde a = 5 e b = - 3
2) f(x) = -2x - 7, onde a = -2 e b = - 7
3) f(x) = 11x, onde a = 11 e b = 0
Gráfico de uma função
Se cada reta interceptar o gráfico em um único ponto, ela
será uma função. Mas , se uma reta interceptar em dois
ou mais pontos, não é Função.

7. Representação gráfica de uma função
• O plano cartesiano composto de duas retas (horizontal
e vertical) que se cruzam em um único ponto,
chamado de origem.
• A coordenadas cartesianas, representando-o por um
par ordenado na forma (x,y).
Localização dos pontos
A(4;3)
B(1;2)
C(-2;4)
D (-3;-4)
E (3;-3)
F (-4;0)

8. Construção do Gráfico
• O jeito mais fácil de se construir uma função de
primeiro grau é criar uma tabela para os valores
de x e determinar os valores associados em y.
y = x + 1
F(x) = x + 1
x y (x,y)
-1 -1+1=0 (-1,0)
0 0+1=1 (0,1)
1 1+1=2 (1,2)
2 2+1=3 (2,3)
3 3+1=4 (3,4)

9. Construção do Gráfico
• O modo mais recomendado na construção de uma
função é encontrar os interceptos em x e em y.
• y = x + 1
• F(x) = x + 1
Para x=0 Para y=0
y= x+1 y=x+1
y=0+1 0=x+1
y=1 x=-1

10. Estudo da função
 Imagine a função afim f(x)= a.x+b e função linear f(x)=ax
 Quando (a>0) , teremos uma função crescente
Gráficos das funções y = x + 2 ; y = x – 3 e y=x;
x
y
0 1 2 3–3 –2 –1
1
2
3
–3
–2
–1
4 5–4–5
–5
–4
4
5
a > 0 y = x – 3
y = x + 2
y = x

11. Estudo da função
 Imagine a função afim f(x)= a.x+b e função linear f(x)=ax
 Quando (a<0), teremos uma função decrescente
Gráficos das funções y=-2x; y = –2x + 4 e y = –2x – 3.
x
y
0 1 2 3–3 –2 –1
1
2
3
–3
–2
–1
4 5–4–5
–5
–4
4
5
y = –2x + 4
y = –2x
a < 0
y = –2x – 3

12. Quando (a=0), teremos uma função constante
Gráfico da função f(x)=3
Estudo da função
a = 0
f(x)=3

13. Zero de uma Função Afim
Encontre o zero da função
f(x)=3x-9, onde f(x)=y=0 ;
3x-9=0
3x = 9
3 3
x = 3
Substituindo o valor no X.
y=3(3)-9
y=9-9
y=0

14. Intersecção
• Em qual ponto as funções y=x+1 e y=-2x+1 se
interceptam?
y= x+1 (I)
y= -2x+1 (II)
x+1= -2x+1
x+2x = 1-1
3x=0
x=0/3
x=0
Substituindo em (I), temos:
y = 0+1
y = 1
Resposta: Nos pontos (0,1) -2
-1
0
1
2
3
4
-5 0 5
Y
Valores
Y

15. "A mudança deve acontecer de dentro para
fora. Os seus pensamentos determinarão
diretamente a forma que você vê o mundo.
Pense positivo! Pense que você pode e que
você é capaz de coisas maiores." (Dr. Jô
Furlan)

16. Bibliografia
• Slidesdare
• Google imagens
• Livro didático Vontade de saber de
matemática
• Artigos relacionados as equações do 2º grau.
• Site Só matemática.

17. Função Polinomial do 2º grau
Prof:Zaqueu Oliveira

18. Objetivos
• Compreender o conceito de função.
• Escrever a lei de formação de uma função
• Identificar a variável dependente e independente.
• Representar uma função por meio de gráficos.
• Classificar as funções em completa ou incompleta.
• Determinar o zero de uma função, o ponto de
interseção de seu gráfico e o vértice da parábola.
• Determinar o ponto de máximo e mínimo.

19. História
•Desde o tempo dos Gregos até à Idade Moderna a
teoria dominante era a Geometria Euclidiana que
tinha como elementos base o ponto, a reta e o plano.
•A noção de função vai ser um dos fundamentos do
Cálculo Infinitesimal. Foi Leibniz (1646 - 1716) quem
primeiro usou o termo "função" em 1673 no
manuscrito Latino "Methodus tangentium inversa, seu
de fuctionibus".
•Um retoque final nesta definição viria a ser dado em
1748 por Euler (1707 - 1783) - um antigo aluno de
Bernoulli - substituindo o termo "quantidade" por
"expressão analítica". Foi também Euler quem
introduziu a notação f(x).

20. Função do 2° Grau
Uma quadra esportiva tem a forma retangular, com 40m de
comprimento e 20m de largura. O clube pretende ampliá-la.
Para isso, vai construir em volta dela uma faixa de largura
constante.
Sua área é função de x.
A = (40 + 2x) . (20 + 2x)
A = 800 + 80x + 40x + 4x2
A = f(x) = 4x² + 120x + 800

21. Chama-se função quadrática, ou função polinomial do 2º grau,
qualquer função f de IR em IR dada por uma lei da forma
f(x) = ax² + bx + c, onde a, b e c são números reais e a ≠ 0.
 a é o coeficiente real de x², com a≠0.
b é o coeficiente real de x.
c é um coeficiente real, também chamado termo independente.
Definição

22. Alguns exemplos de função quadráticas
• Função completa:
f(x) = 3x² - 4x + 1,(completa) onde a = 3, b = - 4 e c = 1
• Função incompleta:
f(x) = x² -1, (incompleta) onde a = 1, b = 0 e c = -1
f(x) = - x² + 8x, (incompleta) onde a = -1, b = 8 e c = 0
f(x) = -4x², (incompleta) onde a = - 4, b = 0 e c = 0

23. Toda função quadrática
quando a > 0 concavidade
voltada para cima.
a) y= x² - x - 6
Quando a < 0 concavidade
voltada para baixo.
b) y= - 3x²
CONCAVIDADE DA PARÁBOLA
O gráfico de uma função polinomial do 2º grau, y = ax² + bx + c,
com a ≠ 0, é uma curva chamada parábola.

25. A parábola está presente em algumas
situações do cotidiano. Quais são elas?
A antena parabólica A forma de parábola

26. Gráfico da função quadrática
• Seja a função definida por y = - x²+ 2x - 2
vamos atribuir para x os valores -1, 0, 1, 2 e 3
calcular os valores de y.
-6
-5
-4
-3
-2
-1
0
-2 0 2 4
Valores Y
Valores Y

27. Gráfico de uma função quadrática
 Todo gráfico de uma função do 2º grau é uma
parábola.
 O gráfico de uma função quadrática é composto de três
partes fundamentais:
1) Zeros da função: é ou são pontos em que o gráfico
corta o eixo das abscissas (eixo x), ou seja , onde y=0.
02) Vértice: ponto mais alto ou mais baixo do gráfico.
03) Termo independente: ponto que o gráfico corta o
eixo das ordenadas (eixo y), Neste ponto x=0.

28. A quantidade de raízes reais de uma função quadrática
depende do valor obtido para o radicando ∆=b²-4.a.c,
chamado discriminante, a saber:
1)Quando ∆>0, é positivo, há duas raízes reais e distintas;
2)Quando ∆=0, é zero, há duas raízes reais e iguais;
3)Quando ∆<0, é negativo, não há raiz real
Zeros ou raízes

29. > 0 , tem dois zeros reais e diferentes.
a > 0 a < 0
> 0,tem dois zeros reais e iguais
a > 0 a < 0
< 0, não tem zeros reais.
a > 0 a < 0

30. Zeros ou Raízes
As raízes são as soluções da equação do 2º grau
ax² + bx + c = 0, as quais são dadas pela chamada fórmula de
Bháskara:
Como determinar a raiz ou zero da Função do 2º grau?
Simplesmente aplicando a resolução de equações do 2º
grau :

31. Zeros ou Raízes
F(x)= x² + x – 6,igualando f(x)=0 => x² + x – 6=0
1) Identificação de coeficientes
onde a=1, b=1 e c=-6
2) ∆=b²-4.a.c
∆= (1)² - 4.(1).(-6) = 1+24 = 25>0
Como ∆>0, a função terá dois zeros.
3)
-8
-6
-4
-2
0
2
4
6
8
-5 0 5
Valores Y

32. Resolução de funções Incompletas
Inequações da forma:
ax² +bx = 0, (c = 0)
De modo geral, a equação do
tipo ax² +bx = 0 tem para
soluções:
x = 0
e
x = - b
a
Inequações da forma:
ax² +c = 0, (b = 0)
De modo geral, a equação
do tipo ax² +c = 0:
possui duas raízes reais se:
- c for um nº positivo
a
não possui raiz real se:
- c for um nº negativo
a

33. O gráfico de uma função quadrática intercepta o eixo
y no ponto de coordenadas (0,c)
Interseção com o eixo y

34. Coordenadas do vértice da parábola
Quando a > 0, a parábola tem
concavidade voltada para cima e um
ponto de mínimo V
Quando a < 0, a parábola tem
concavidade voltada para baixo e
um ponto de máximo V.

35. "A mudança deve acontecer de dentro para
fora. Os seus pensamentos determinarão
diretamente a forma que você vê o mundo.
Pense positivo! Pense que você pode e que
você é capaz de coisas maiores." (Dr. Jô
Furlan)

36. Bibliografia
• Slidesdare
• Google imagens
• Livro didático Vontade de saber de
matemática
• Artigos relacionados as equações do 2º grau.
• Site Só matemática.