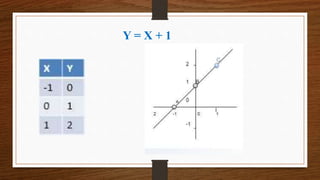
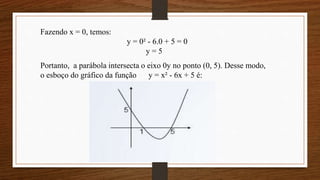
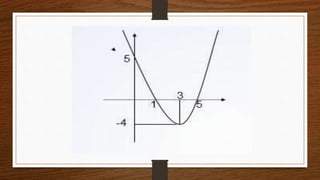
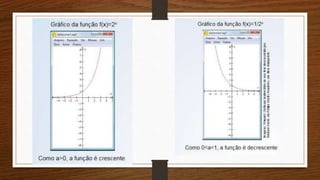
O documento apresenta os conceitos de funções afim, quadrática e exponencial, incluindo suas definições, gráficos e propriedades. Exemplos ilustram como essas funções podem ser usadas para modelar situações do cotidiano e resolver problemas envolvendo taxímetros, crescimento de populações bacterianas e sistemas de equações.

1. Estudo das Funções
• Função Afim ou
Linear (1º grau)
• Função
Quadrática (2º
grau)
• Função
Exponencial

2. Para que estudar as Funções?
•Em nosso dia-a-dia, estamos sempre
comparando e relacionando
números, grandezas e formas.

3. Exemplos
Número de questões que acertei num teste, com a nota que vou
tirar;
Velocidade média do automóvel, com o tempo de duração de
uma viagem;
Número de pães que vou comprar, com o preço a pagar.

4. Para fazer esta tabela, a dona Ana
faz o seguinte cálculo:
Preço a pagar = 0,20. nº de pães.
Dizemos que o preço a pagar (y) é
função do número de pães (x), pois
para cada quantidade de pães existe
um único preço y a pagar.
Y = 0,20.x
Na padaria da Ana tem uma tabela para facilitar o trabalho do
caixa:

5. Função Afim e Linear
1º Grau

6. Definição de Função Afim (1º Grau)
Uma função f: R→R chama-se função afim,
quando existem dois números reais a e b que
f(x) = ax + b. Para todo x ϵ R.

7. Gráfico da Função Afim
• Podemos representar os
pares ordenados no plano
cartesiano e fazer o gráfico
da função.

8. Y = X + 1

9. Questão 1
Em uma certa cidade, os
taxistas cobram R$2,50, a
bandeirada, mais R$1,50
por quilômetro rodado.
Como é possível para um
passageiro determinar o
valor da corrida?

10. Resolução
Podemos verificar que o valor
cobrado é sempre R$ 2,50, somado
com R$1,50 e multiplicado pela
quantidade de quilômetros rodados.
Considerando x a quantidade de
quilometro e y o valor cobrado,
temos: Y = 1,50x + 2,50

11. Gráfico da Função

12. Função Quadrática
2º grau

13. Definição de Função Quadrática (2º grau)
Seja a, b e c números reais e a ≠ 0. A função f :R→R tal
que f(x) = ax² + bx + c para todo x Є R, é chamada
função polinomial do 2º grau ou função quadrática.

14. Exemplos
•y = 5x² - 3x + 8
•y = -2x² + x
•g(x) = x² - 3

15. Gráfico da Função do 2º grau
f(x)= x² :
Como na função do 1º grau,
basta atribuir valores reais
para x, obtemos seus valores
correspondentes para y.

16. Raízes da Função
Chama-se zeros ou raízes da função polinomial do 2º grau f(x) = ax² + bx +c,
a ≠ 0, os números reais x tais que f(x) = 0.
Então as raízes da função são as soluções da equação do 2º
grau, as quais são dadas pela chamada fórmula de Bhaskara:
2.a
4.a.c-b²±b
x



17. Observação
A quantidade de raízes reais de uma função quadrática depende do
valor obtido para o radicando , chamado discriminante, a saber:
quando é positivo, há duas raízes reais e distintas;
quando é zero, há só uma raiz real;
quando é negativo, não há raiz real.




18. PONTO DE INTERSECÇÃO DA PARÁBOLA COM
O EIXO 0y
Para obter esse ponto, atribuímos o valor zero à variável x da equação da
parábola f(x) = ax² + bx +c
y = a.0² + b.0 + c
y = c
Logo, o ponto de intersecção da parábola com o eixo oy é (0, c).

19. Para esboçar o gráfico da função y = x² - 6x + 5, vamos obter os pontos de
intersecção da parábola com os eixos 0x e 0y .
Fazendo y = 0, achamos as raízes:
Assim, a parábola intersecta o eixo 0x nos pontos (1, 0) e (5, 0).

20. Fazendo x = 0, temos:
y = 0² - 6.0 + 5 = 0
y = 5
Portanto, a parábola intersecta o eixo 0y no ponto (0, 5). Desse modo,
o esboço do gráfico da função y = x² - 6x + 5 é:

21. Máximo e Mínimo da Função Quadrática
Quando a > 0, a parábola tem concavidade voltada para
cima e um ponto de mínimo V; quando a < 0, a parábola
tem concavidade voltada para baixo e um ponto de
máximo V.

22. Máximo e Mínimo da Função Quadrática
Em qualquer caso, as coordenadas de V são . Veja os gráficos:)
4
,
2
(
aa
b 


23. Exemplo
O vértice da parábola da equação y = x² - 6x + 5 é dado por V(Xv, Yv), em
que:
Portanto o vértice da parábola é o ponto v(3, -4).

25. Questão 2
• Há dois números em que o triplo do quadrado é igual a 15 vezes esses
números. Quais números são esses?

26. Função Exponencial

27. Definição de Função Exponencial
•É uma função f: , definida por f(x)=ax ou y=ax,
que atende as seguintes restrições a > 0 e a ≠ 1.

28. Gráfico da Função Exponencial
Gráfico de uma função é o desenho da relação existente entre dois objetos
“X e Y” e no caso da Função Exponencial, essa relação apresenta a seguinte
característica:
se a > 1 “Função Crescente”
se 0 < a < 1 “Função Decrescente”, onde “a” representa a base da função:
f(x)=ax ou y=ax.

30. Questão 3
• Uma cultura, inicialmente com 100 bactérias, reproduz-se em
condições ideais. Suponha que, por divisão celular, cada bactéria
dessa cultura dê origem a duas outras bactérias idênticas por hora.
1. Qual a população dessa cultura após 3 horas do instante inicial?
2. Depois de quantas horas a população dessa cultura será de 51200
bactérias?