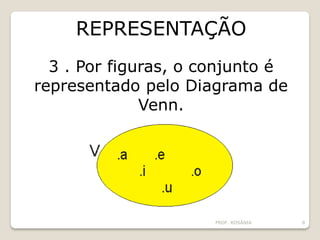
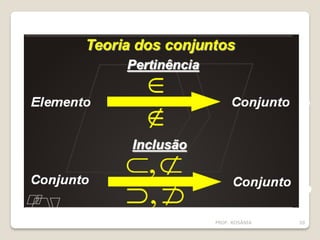
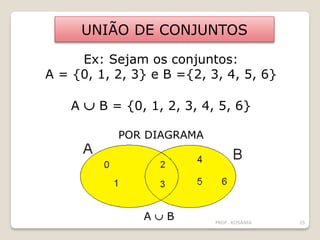
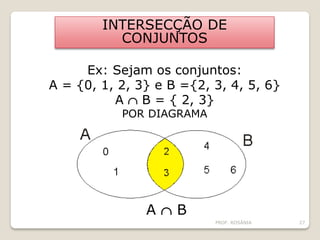
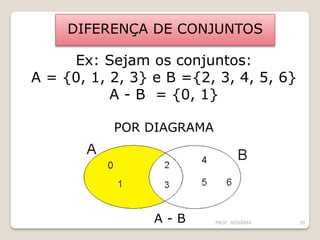
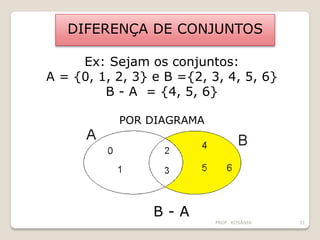
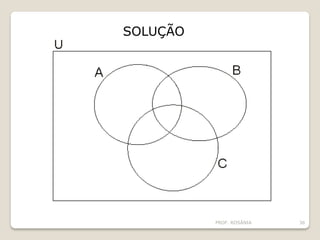
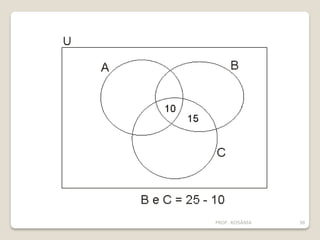
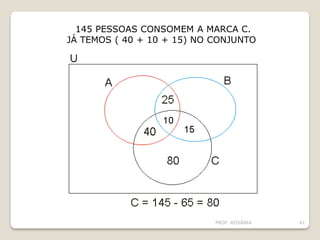
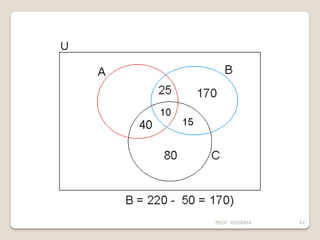
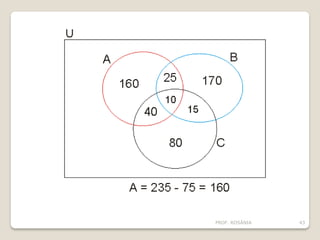
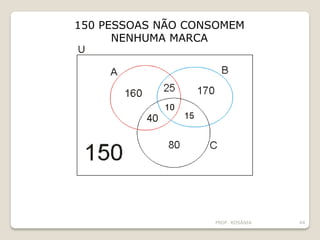
O documento descreve os conceitos básicos de conjuntos, incluindo elementos, representação de conjuntos, pertinência, igualdade, subconjuntos, conjunto vazio, conjunto unitário, conjunto universo, conjunto das partes e operações com conjuntos como união, interseção e diferença. É apresentado um problema sobre consumo de margarinas para ilustrar o cálculo do tamanho de um conjunto universo.

1. CONJUNTOS
É um agrupamento de
números, objetos, pessoas,
animais ou coisas
PROF. ROSÂNIA
1

2. Os itens que formam o conjunto
são chamados de ELEMENTOS e
são representados por letras
minúsculas.
(a, b, c....)
PROF. ROSÂNIA 2

3. Para nomear um conjunto
utilizamos letras
MAIÚSCULAS.
A = {a, b, c, ...}
PROF. ROSÂNIA 3

4. PROF. ROSÂNIA 4
1 . Por extenso, quando
seus elementos são
enumerados entre chaves e
separados por vírgula
V= {a, e, i, o, u}

5. Obs: Se o número de
elementos do conjunto for
muito grande, escreve-se
os três primeiros elementos
seguidos de reticências e
então escrevemos os três
últimos elementos.
L = { a, b, c, ..., x, y, z}
PROF. ROSÂNIA 5

6. Obs: No caso do
conjunto for infinito,
escrevemos seus
primeiros elementos
seguidos de reticências.
N = { 0, 1, 2, 3, 4, ...}
PROF. ROSÂNIA 6

7. 2 . Por Descrição, o conjunto é
representado por uma
propriedade que caracteriza
todos os seus elementos.
V= {x/x é vogal do alfabeto}
REPRESENTAÇÃO
PROF. ROSÂNIA 7

8. REPRESENTAÇÃO
3 . Por figuras, o conjunto é
representado pelo Diagrama de
Venn.
PROF. ROSÂNIA 8

9. PERTINÊNCIA
A relação entre ELEMENTO e
CONJUNTO é uma relação de
pertinência. Se o elemento x
pertence ao conjunto A, então
escrevemos:
x  A (lê-se: x pertence a A)
PROF. ROSÂNIA 9

10. PERTINÊNCIA
Se o elemento x não
pertence ao conjunto A,
então escrevemos:
x  A (lê-se: x não
pertence a A)
PROF. ROSÂNIA 10

11. Utilizamos os símbolos 
(pertence) e  (não
pertence) para
relacionar elemento
com conjunto.
PROF. ROSÂNIA 11

12. IGUALDADE DE CONJUNTOS
Se dois conjuntos possuem os
mesmos elementos, então eles são
iguais. Ex:
A={a, b, c, d} e B={d, c, b, a}
A = B
Todo elemento de A pertence a B e
vice-versa.
PROF. ROSÂNIA 12

13. Entretanto, se dois
conjuntos A e B não
possuem os mesmos
elementos, dizemos que
eles não são iguais, ou
melhor, dizemos que
A ≠ B
PROF. ROSÂNIA 13

14. CONJUNTO VAZIO
É o conjunto que não possui
elementos, sendo
representado por:
{ } ou 
PROF. ROSÂNIA 14

15. CONJUNTO UNITÁRIO
É o conjunto que possui
apenas um elemento.
PROF. ROSÂNIA 15

16. CONJUNTO UNIVERSO
É o conjunto ao qual
pertencem os elementos de
todos os conjuntos
envolvidos no estudo.
PROF. ROSÂNIA 16

17. SUBCONJUNTO
Se todo elemento de um conjunto A
pertence também ao conjunto B, então
dizemos que A é subconjunto de B.
Então dizemos que A é subconjunto de
B.
Escrevemos: A  B ( lê-se: A está
contido em B).
Podemos, neste caso, dizer que B
contém A (B  A)
PROF. ROSÂNIA 17

18. SUBCONJUNTO
Se A não for subconjunto de B,
então dizemos que:
A  B ( A não está contido em
B)
B  A ( B não contém A)
PROF. ROSÂNIA 18

19. As expressões contém ( ),
não contém (), está
contido (), e não está
contido () são utilizadas
apenas para relacionar
conjunto com conjunto.
PROF. ROSÂNIA 19

20. Elemento Conjunto
Conjunto Conjunto
PROF. ROSÂNIA 20

21. CONJUNTO DAS PARTES
O conjunto de todos os subconjuntos
de um conjunto.
conjunto de partes de A é denotado
por P(A).
PROF. ROSÂNIA 21

22. Seja A = { x, y, z} a lista completa de
subconjuntos de A é:
•{ } (conjunto vazio);
•{x};
•{y};
•{z};
•{x, y};
•{x, z};
•{y, z};
•{x, y, z};
e portanto o conjunto de partes de A é o
conjunto de 8 elementos:
P(S) = {{ }, {x}, {y}, {z}, {x, y}, {x, z},
{y, z}, {x, y, z}}.
PROF. ROSÂNIA 22

23. OPERAÇÕES COM
CONJUNTOS
São três as operações com conjuntos:
UNIÃO
INTERSECÇÃO
DIFERENÇA
PROF. ROSÂNIA 23

24. UNIÃO DE CONJUNTOS
A união de dois conjuntos A
e B, é o conjunto constituído
por todos os elementos que
pertencem a A ou a B e é
representada por A  B
(lê-se: A união B).
PROF. ROSÂNIA 24

25. UNIÃO DE CONJUNTOS
Ex: Sejam os conjuntos:
A = {0, 1, 2, 3} e B ={2, 3, 4, 5, 6}
A  B = {0, 1, 2, 3, 4, 5, 6}
POR DIAGRAMA
A  B PROF. ROSÂNIA 25

26. INTERSECÇÃO DE
CONJUNTOS
A intersecção de dois
conjuntos A e B é o conjunto
constituído pelos elementos
que pertencem ao conjunto A
e ao conjunto B.
É representado por:
A  B (lê-se: A intersecção B).
PROF. ROSÂNIA 26

27. INTERSECÇÃO DE
CONJUNTOS
Ex: Sejam os conjuntos:
A = {0, 1, 2, 3} e B ={2, 3, 4, 5, 6}
A  B = { 2, 3}
POR DIAGRAMA
A  B
PROF. ROSÂNIA 27

28. INTERSECÇÃO DE
CONJUNTOS
OBS: se não houver elementos
que pertençam simultaneamente
aos dois conjuntos A e B, dizemos
que a intersecção entre A e B é o
conjunto vazio.
A  B = 
Neste caso A e B são conjuntos
DISJUNTOS
PROF. ROSÂNIA 28

29. DIFERENÇA DE CONJUNTOS
A diferença entre dois
conjuntos A e B, é o conjunto
formado pelos elementos que
pertencem a A, mas não
pertencem a B.
A – B ( lê-se: A menos B)
PROF. ROSÂNIA 29

30. DIFERENÇA DE CONJUNTOS
Ex: Sejam os conjuntos:
A = {0, 1, 2, 3} e B ={2, 3, 4, 5, 6}
A - B = {0, 1}
POR DIAGRAMA
A - B PROF. ROSÂNIA 30

31. DIFERENÇA DE CONJUNTOS
Ex: Sejam os conjuntos:
A = {0, 1, 2, 3} e B ={2, 3, 4, 5, 6}
B - A = {4, 5, 6}
POR DIAGRAMA
B - A
PROF. ROSÂNIA 31

32. Se B for um subconjunto de A (B  A), a
diferença A – B chama-se complementar
de B em relação a A, e é representada
por
Lê-se: Complementar de B em relação a A.
COMPLEMENTO DE UM
CONJUNTO
PROF. ROSÂNIA 32

33. Ex: considere os conjuntos
A = { 0, 1, 2, 3} e B = { 0, 1}
temos: = A – B = {2, 3}
Por diagrama:
PROF. ROSÂNIA 33

34. PROF. ROSÂNIA 34
PROBLEMAS
1. Em certa região foi realizada uma
pesquisa sobre o consumo de margarina
das marcas A, B e C. Os dados obtidos
nessa pesquisa estão na tabela a seguir.

35. PROF. ROSÂNIA 35
a)500
b)650
c) 700
d)850
Com base nesses dados assinale o
número de pessoas que responderam
a essa pesquisa.

36. PROF. ROSÂNIA 36
SOLUÇÃO

37. PROF. ROSÂNIA 37

38. PROF. ROSÂNIA 38

39. PROF. ROSÂNIA 39

40. PROF. ROSÂNIA 40

41. PROF. ROSÂNIA 41
145 PESSOAS CONSOMEM A MARCA C.
JÁ TEMOS ( 40 + 10 + 15) NO CONJUNTO

42. PROF. ROSÂNIA 42

43. PROF. ROSÂNIA 43

44. PROF. ROSÂNIA 44
150 PESSOAS NÃO CONSOMEM
NENHUMA MARCA

45. PROF. ROSÂNIA 45
Para saber o número de pessoas que
responderam à pesquisa, basta somar todos
os elementos, ou seja:
160 + 25 + 10 + 40 + 170 + 15 + 80 + 150
U = 650 pessoas
a)500
b)650
c)700
d)850