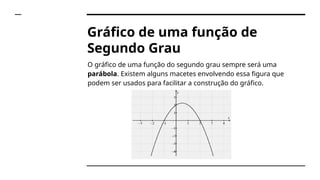
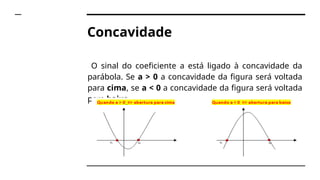
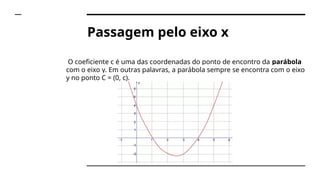
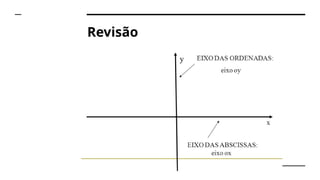
Uma função de segundo grau é expressa na forma y = ax² + bx + c, com a diferente de zero. As raízes podem ser reais ou inexistentes, determinadas pela fórmula de Bhaskara e pelo discriminante (delta). O gráfico é uma parábola, cuja concavidade depende do sinal de a e as raízes correspondem aos pontos onde a parábola cruza o eixo x.

1. Função de Segundo
Grau

2. O que é função?
Uma função é uma regra que liga
cada elemento de um conjunto A
a um único elemento de um
conjunto B, respectivamente
conhecidos como domínio e
contradomínio da função.

3. Função de Segundo Grau
Para que a função seja chamada função do segundo
grau, é necessário que sua regra (ou lei de formação)
possa ser escrita na seguinte forma:
y = ax²+ bx + c
com a sempre diferente de zero!

4. Identificando Funções de 2º
grau
a) y = x² + 3x - 5
b) y = -5x² +2
c) f(x) = 3x²+2x - 3
d) x = -10y²
e) y = 3x + 3
f) y = 2 + 3x² - 2x
Quais dessas funções acima são funções de
segundo grau?

5. Raízes das funções de Segundo
Grau
As raízes de uma função são os valores assumidos por
x quando f(x) = 0.
Em funções de segundo grau podermos ter:
● 2 raízes reais;
● 1 raíz real;
● nenhuma raíz real;

6. Fórmula de Bhaskara
Temos as seguintes situações:
Delta positivo: teremos duas raízes reais;
Delta igual a zero: teremos uma raíz real;
Delta negativo: não há nenhuma raíz real;

7. Exemplos
a) f(x) = x
2
+ x – 6
b) f(x) = x² + 3x – 10
c) f(x) = 3x² - 5x
d) f(x) = 4129247249187x²
e) f(x) = x²-9

8. Ponto máximo ou mínimo
(Vértice)
Vamos recalcular os vertices
para as funções do slide
anterior?

9. Gráfico de uma função de
Segundo Grau
O gráfico de uma função do segundo grau sempre será uma
parábola. Existem alguns macetes envolvendo essa figura que
podem ser usados para facilitar a construção do gráfico.

10. Concavidade
O sinal do coeficiente a está ligado à concavidade da
parábola. Se a > 0 a concavidade da figura será voltada
para cima, se a < 0 a concavidade da figura será voltada
para baixo.

11. Passagem pelo eixo x
O coeficiente c é uma das coordenadas do ponto de encontro da parábola
com o eixo y. Em outras palavras, a parábola sempre se encontra com o eixo
y no ponto C = (0, c).

12. Localização das raízes reais
As raízes da função serão representadas por
pontos onde a parábola cruza com o eixo x!

13. Revisão