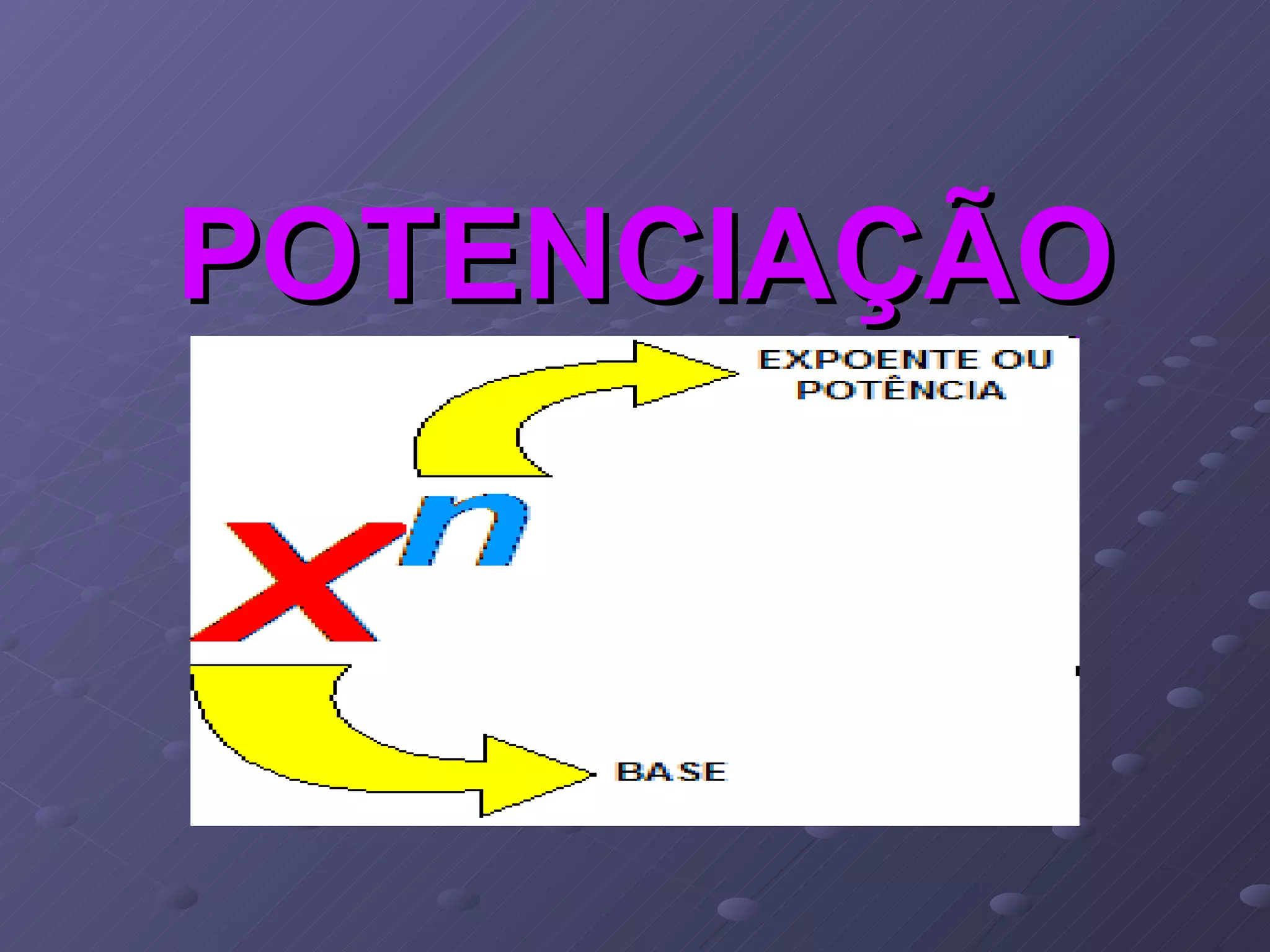
1) O documento explica o que são potências e como calcular operações com potências como multiplicação, divisão, potenciação e raiz de potências. 2) É dado que para multiplicação de bases iguais soma-se os expoentes e para divisão subtrai-se. 3) Também é explicado como calcular potenciação de potência e potência de produto.

1. POTENCIAÇÃO

2. O QUE SÃO AS POTÊNCIAS: As potências surgiram no intuito de representar multiplicações onde os fatores eram iguais. Exemplo: 3 x 3 x 3 x 3 é o 3 vezes ele mesmo 4 vezes Multiplicação com Fatores iguais

3. Representamos uma potência da seguinte forma: base expoente 3 4 =3 x 3 x 3 x 3 = 81 Chamamos de: base sempre valor do fator ; expoente é a quantidade de vezes que o fator se multiplica; potência é o resultado do produto.

4. Casos especiais: EXPOENTES: 1: Toda potenciação cujo expoente é 1 tem como resultado o valor da base. Exemplo: 7 1 = 7 0 : Toda potenciação cujo expoente é zero o resultado será sempre 1. Exemplo: 12 0 = 1

5. Base: 10: P ara calcular uma potenciação com base igual a dez basta escrever zeros igual ao número do expoente. Exemplo: 10 8 = 100.000.000 (8 zeros) Ou seja 10 5 = 100.000 5 zeros

6. Multiplicação entre Bases Iguais A Regra é: Repete a Base e SOMA os Expoentes . Exemplos : 2 2 . 2 3 = 2 2 + 3 = 2 5 = 2 x 2 x 2 x 2 x 2 = 32 5 1 . 5 3 = 5 1 + 3 = 5 4 = 5 x 5 x 5 x 5 = 625

7. Divisão entre Bases Iguais A Regra é: Repete a Base e SUBTRAI os Expoentes . Exemplos : 2 8 ÷ 2 3 = 2 8- 3 = 2 5 = 2 x 2 x 2 x 2 x 2 = 32 5 7 . 5 3 = 5 7-3 = 5 4 = 5 x 5 x 5 x 5 = 625

8. Observação: Muitas vezes as divisões são escritas na forma fracionária, porém aplica-se a mesma regra da divisão. Detalhe: expoente do numerador menos expoente do denominador Exemplo:

9. Potência de Potência Regra é: Repete a Base e MULTIPLICA-SE os Expoentes Exemplos: (8 5 ) 6 = 8 5x6 = 8 30 (15 3 ) 9 = 15 3x9 = 15 27

10. Potência de um Produto Regra: DISTRIBUIR a Potência para as Bases Exemplos: (14 x 9) 5 = 14 5 x 9 5 (21 x 3) 8 = 21 8 x 3 8

11. Atividades: Use as propriedades de potencias nas expressões. a) 73 . 75 b) 53 . 54 . 52 c) 105 : 105 d) 45 : 43 e) (52)5 [(56)0]8 (7 . 10)3 ( 2 . 32 . 52)4

12. Agora ficou faço, então mãos a obra!!

13. 3 - Reduza a uma só potencia: a) (-3)⁵ . (-3)² b) (-8) . (-8) . (-8) c) (-5)³ . (-5) . (-5)² d) (-3)⁷ : (-3)² e) (-4)² : (-4)² f) [(-4)² ]³ g) [(-3)³ ]² h) [(-5)⁰ ]³