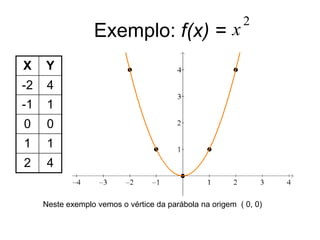
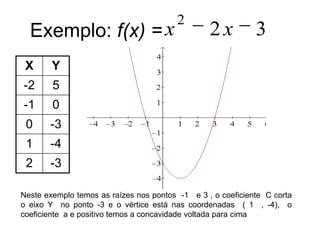
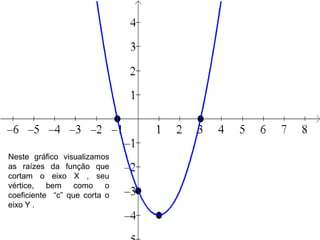
O documento descreve como criar gráficos de funções quadráticas. Todo gráfico de uma função quadrática será uma parábola. Primeiro, tabelamos os valores de x e y de acordo com a função. Devemos observar o coeficiente a para determinar a concavidade da parábola. O documento fornece exemplos de funções quadráticas e como identificar suas raízes, vértice e intercepto no eixo y.

1. Gráfico da Função Quadrática

2. Todo gráfico de uma função do segundo grau será uma parábola .O processo de criação de gráfico é o mesmo para uma função do 1° grau, primeiro tabelamos as coordenadas , obedecendo a função e determinando os valores de x e y Neste caso temos que sempre observar ao tabelar o x e y , o coeficiente a que determina a concavidade da parábola.

3. Exemplo: f(x) = Neste exemplo vemos o vértice da parábola na origem ( 0, 0)

4. Exemplo: f(x) =Neste exemplo temos as raízes nos pontos -1 e 3 , o coeficiente C corta o eixo Y no ponto -3 e o vértice está nas coordenadas ( 1 , -4), o coeficiente a e positivo temos a concavidade voltada para cima

5. Valores das constantes Esta tabela e muito importante no desenvolvimento e entendimento de uma função quadrática.

6. 2° método:Achar as raízes da funçãoO valor de c toca o eixo do yAchar o vértice da funçãoNeste método desenvolvemos a equação de 2º grau , encontrando as raízes x’ e x’’ , temos também o método de encontrar o vértice da parábola.

7. Neste gráfico visualizamos as raízes da função que cortam o eixo X , seu vértice, bem como o coeficiente “c” que corta o eixo Y .