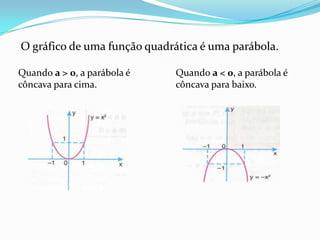
O documento explica o que são funções quadráticas e como representá-las graficamente. Uma função quadrática relaciona uma variável x com outra variável y através da equação y = ax2 + bx + c, onde a, b e c são constantes. O gráfico de uma função quadrática é uma parábola, que pode ser côncava para cima ou para baixo dependendo dos valores de a. O documento apresenta exemplos de como calcular o vértice, raízes e domínios de sinal de funções quadráticas.

1. Função QuadráticaA função do 2º grau

2. Uma quadra esportiva tem a forma retangular, com 40m de comprimento e 20m de largura. O clube pretende ampliá-la. Para isso, vai construir em volta dela uma faixa de largura constante.Sua área é função de x.A = (40 + 2x) . (20 + 2x)A = 800 + 80x + 40x + 4x2A = f(x) = 4x2 + 120x + 800Função quadrática ou função do 2º grau é toda função real do tipoy = f(x) = ax2 + bx + cSendo a, b e c constantes reais, com a ≠ 0

3. O gráfico de uma função quadrática é uma parábola.Quando a > 0, a parábola é côncava para cima. Quando a < 0, a parábola é côncava para baixo.

4. O logotipo de uma empresa foi criado a partir de um quadrado dividido em 8 partes iguais, conforme indica a figura. A área de cada parte é função do lado do quadrado; portanto, a área pintada de vermelho é função do lado do quadrado. Fórmula e gráfico da função do 2º grauRepresentando por x a medida do lado do quadrado e por y a área da parte vermelha, temos a fórmula:

5. Vamos obter alguns pontos do gráfico atribuindo valores para x.Observe, abaixo, o gráfico de y = 0,25 x2, para x ≥ 0

6. Vamos considerar que a função seja válida para todo x real. Atribuindo valores simétricos aos da tabela anterior, obtemos:

7. Contextualizando Os formandos do ensino fundamental reuniram-se e planejaram uma viagem para comemorar a formatura. A agência de turismo oferece o seguinte pacote promocional: o preço p para cada um será: p = 180 – 0,6x reais.Quanto a agência vai receber para promover a viagem?Se x alunos aderirem, cada um pagando p reais, a receita (R) será x.p; logo, x.(180 – 0,6x).A receita é função do número x de aluno que viajarem. R(x) = - 0,6x + 180xA agência terá receita máxima se forem 150 alunos.

8. Vértice da parábolaÉ o ponto em que o eixo de simetria corta a parábola.Em y = - 0,6x2 +180x , v é o ponto de coordenadas (150,13500)V = (150 , 13500)O valor máximo de y é 13500, que será a receita máxima da agência.Vamos representar por xv a abscissa do vértice eyva ordenada do vértice.V = (xv , yv)Os zeros da função quadrática (raízes da função)Zeros de uma função f são os valores de x para os quais f(x) = 0

9. Os sinais da função quadráticaObservemos o gráfico da função y = x2 – 4x + 3.Os zeros de f , 1 e 3 , são as abscissas dos pontos em que a parábola corta o eixo x.Para todos os valores de x menores que 1, temos f(x) > 0Para x = 1 ou x = 3, temos f(x) = 0.Para os valores de x entre 1 e 3 , temos f(x) < 0Para todos os valores de x maiores que 3 , temos f(x) > 0f(x) > 0, para x < 1 ou x > 3f(x) = 0, para x = 1 ou x = 0f(x) < 0, para 1 < x < 3

10. Construção de uma parábolaSendo a função f(x) = x2 – 2x + 21º passo:Determinar as raízes3º passo: Determinar onde a parábola corta o eixo ordenado(termo independente da função = c) e o seu simétrico em relação ao eixo de simetria.x2 – 2x + 2 = 0∆= b2 – 4ac∆= - 4x = s= { } (não existe raiz real)4º passo:Marcar os pontos no gráfico e traçar a curva2º passo: Determinar xv e yv.

11. BibliografiaPanadésRubió, Angel; Freitas, Luciana Tenuda de. Matemática e sua tecnologias: ensino médio. Vol. 1. ed.1 – São Paulo: IBEP, 2005Iezzi, Gelson; Dolce, Osvaldo; Machado, Antônio. Matemática e Realidade: 9º Ano 6ª ed.São Paulo: Atual, 2009