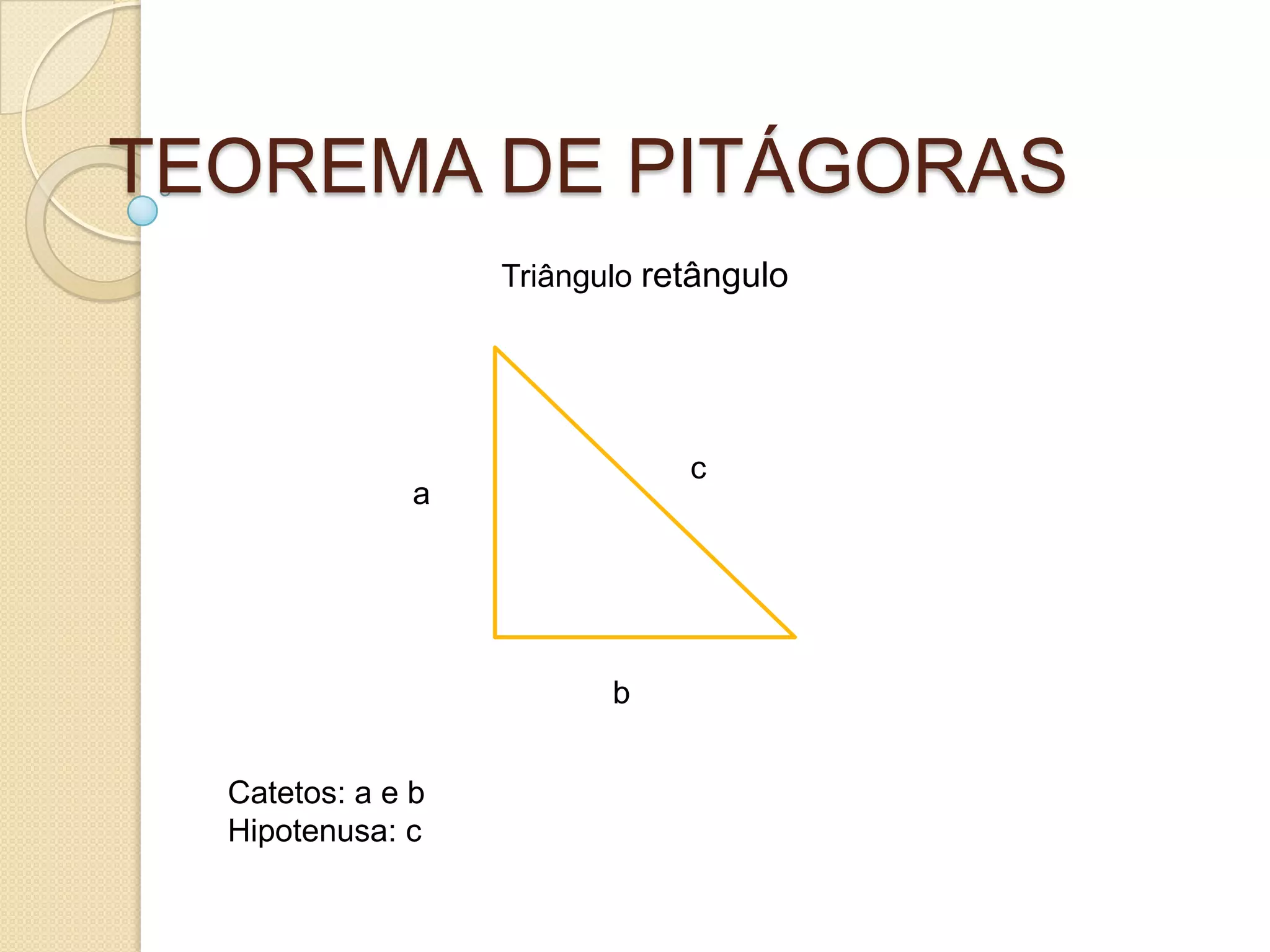
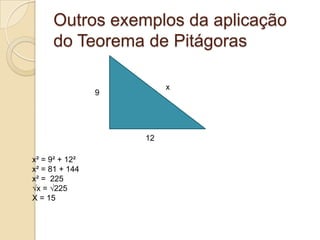
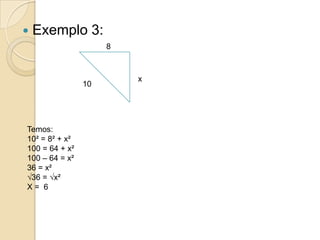
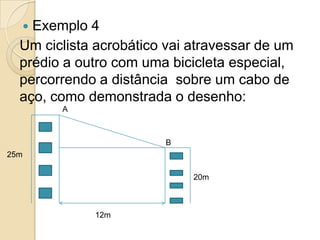
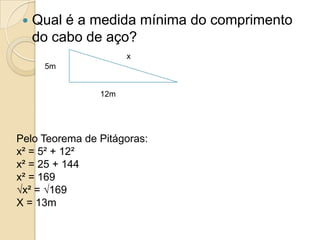
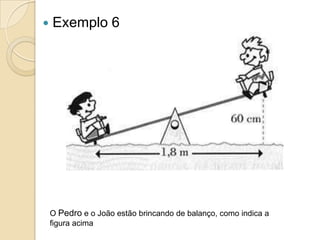
O documento apresenta o Teorema de Pitágoras e sua aplicação para calcular lados desconhecidos em triângulos retângulos. O teorema relaciona os catetos e a hipotenusa de um triângulo retângulo da seguinte forma: a2 + b2 = c2. Exemplos ilustram como usar o teorema para resolver problemas geométricos.