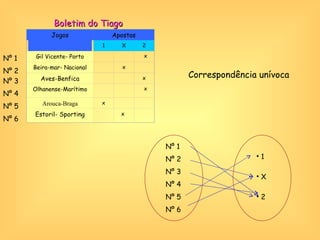
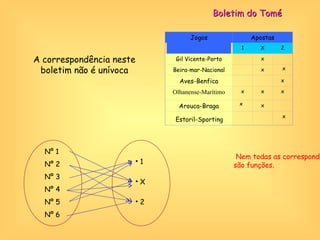
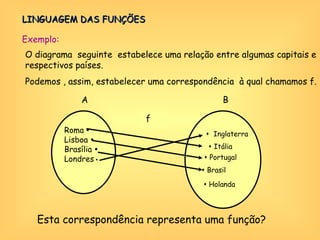
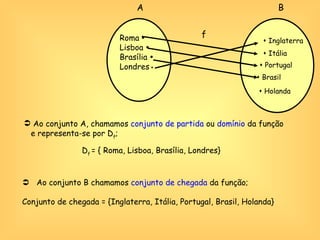
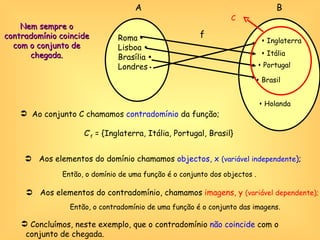
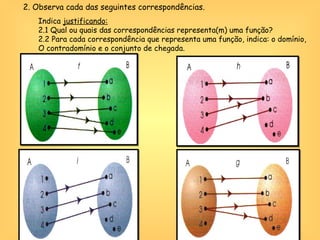
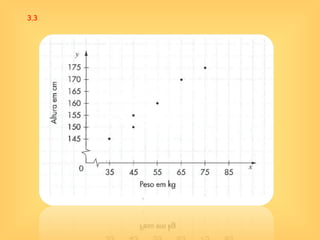
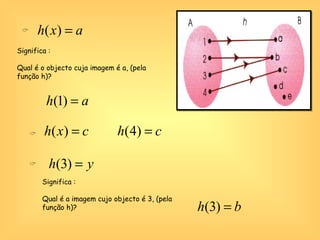
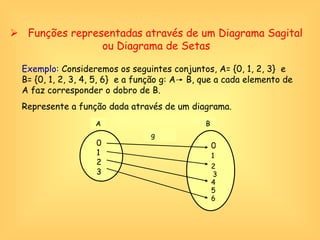
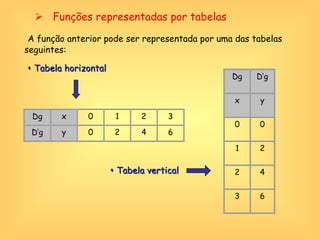
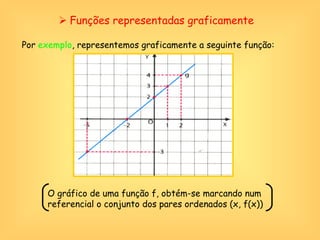
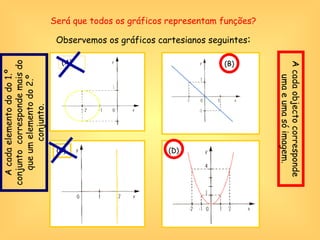
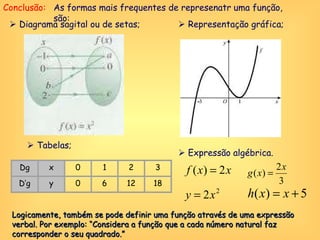
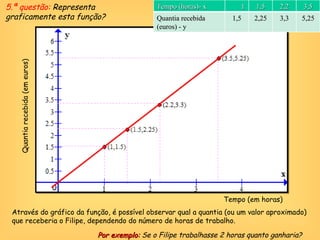
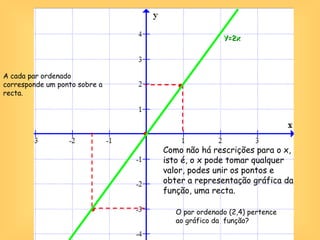
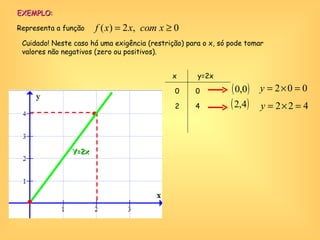
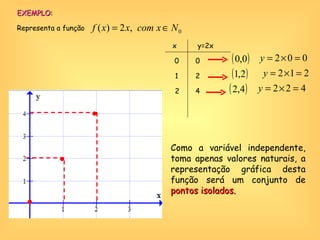
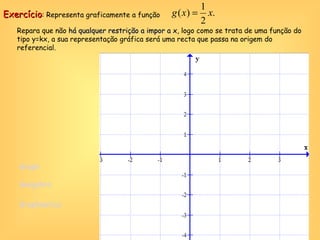
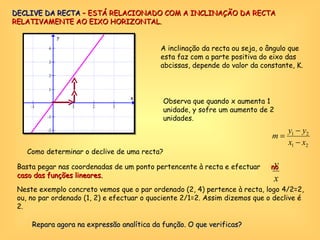
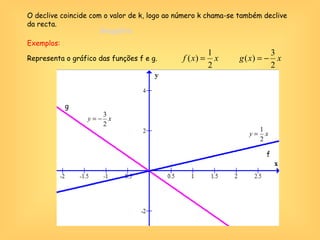
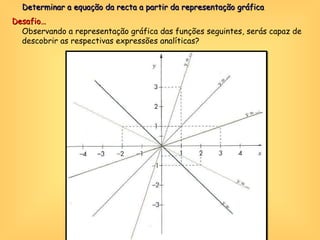
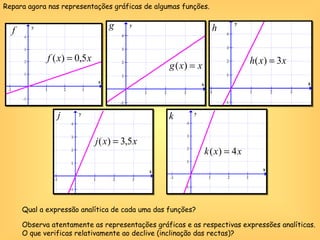
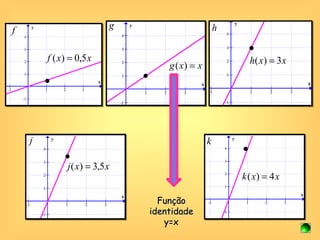
O documento discute o conceito de função em matemática, sua história e importância. Explica que funções relacionam variáveis dependentes e independentes e podem ser representadas de diferentes formas, incluindo diagramas, tabelas, gráficos e expressões algébricas. Funções desempenham um papel fundamental em diversas áreas como economia e física.