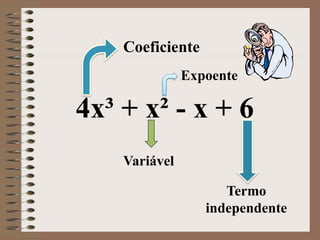
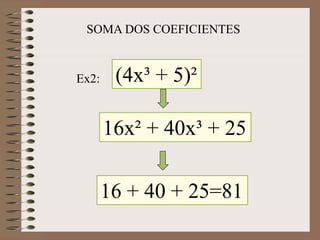
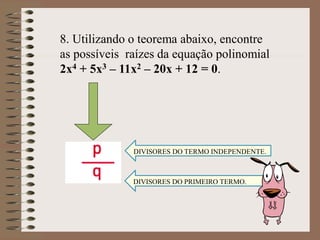
1) O documento apresenta conceitos sobre polinômios como classificação, operações e propriedades. 2) São definidos termos como monômio, binômio, trinômio, polinômio, grau, coeficiente e variável. 3) São explicados procedimentos para realizar operações como adição, subtração, multiplicação e divisão com polinômios.

2. POLINÔMIO é toda expressão
algébrica racional inteira.
Exemplos:
a) -8x³y monômio
b)x²y + 5xw binômio
c) - x + y – 3w trinômio
d)a – b – 2c + 7d polinômio
Classificação especial

3. Função polinomial
ou polinômio
P(x) = anxn + an-1xn-1 + ... +
a2x2 + a1x + a0

4. 4x³ + x² - x + 6
Coeficiente
Variável
Expoente
Termo
independente

5. Grau de um polinômio
Os polinômios são chamados
conforme o seu grau. Para
identificar o seu grau, basta
observar o grau do maior
monômio, esse será o grau
do polinômio.

6. GRAU DE UM POLINÔMIO
EXEMPLOS:

7. GRAU DE UM POLINÔMIO

8. EXPRESSÕES QUE NÃO SÃO
POLINÔMIOS

9. VALOR NUMÉRICO
DE UM POLINÔMIO
Dado um polinômio p(x),
temos que seu valor numérico
é tal que x = a é um valor que
se obtém substituindo x por a,
onde a pertence ao conjunto
dos números reais.

10. VALOR NUMÉRICO DE UM
POLINÔMIO

11. RAIZ DE UM POLINÔMIO
Raízes de um polinômio
são valores que
substituídos nas
variáveis e zeram o
polinômio.

12. Se, ao calcularmos o valor numérico de
um polinômio determinarmos p(a) = 0,
temos que esse número dado por a
corresponde à raiz do polinômio p(x).
RAIZ DE UM POLINÔMIO

13. ENTÃO -1 É RAIZ DE P(X)
OBS: o grau do polinômio indica
o número de raízes, uma delas é o -1.
RAIZ DE UM POLINÔMIO

14. 1 e 0 não são raízes de P(x)
RAIZ DE UM POLINÔMIO

15. RAIZ DE UM POLINÔMIO

16. Então 1 é raíz de P(x)
4º grau
RAIZ DE UM POLINÔMIO

17. SOMA DOS COEFICIENTES
x3 + 2x + 2
1 + 2 + 2 = 5
Ex:

18. (4x³ + 5)²
SOMA DOS COEFICIENTES
Ex2:
16x² + 40x³ + 25
16 + 40 + 25=81

19. Regra básica

20. (2𝑥 − 3)102Ex2:
(2.1 − 3)102
= 1

21. PESQUISA DE RAÍZES RACIONAIS
Considerando “p” os divisores do termo
independente e “q” os divisores do
coeficiente do termo de maior grau, as
possíveis raízes racionais deste
polinômio são dadas por:
DIVISORES DO TERMO INDEPENDENTE.
DIVISORES DO PRIMEIRO TERMO.

22. EXEMPLO:
CADA TERMO DE P DIVIDO COM TODOS DE Q
ESSE CONJUNTO SÃO AS POSSÍVEIS
RAÍZES DE P(X)

24. 1. Calcular o valor numérico
do polinômio P(x) = x3 – 7x2 +
3x – 4 para x = 2.
EXERCICIO 1
2. Considerando que p(x) = 2x³ –
kx² + 3x – 2k, para que valores de
k temos p(2) = 4?

25. MONÔMIO COEFICIENTE PARTE
LITERAL
GRAU
4x²y
- 3ab4
2h²z5
2
3
𝑚²𝑛³𝑦
−
1
5
𝑎²𝑏³𝑐
3. Identifique o coeficiente, a parte literal e o dê
grau dos monômios abaixo:

26. 4. Associe V ou F a cada sentença:
( ) 6x² e -4x³ não são monômios semelhantes
( ) 5y e – 5y são monômios opostos
( ) x e 5x são monômios semelhantes
( ) 2 e -7 não são monômios semelhantes.
5. Determine a soma dos coeficientes do
polinômio P(x) = (6x² – 4x + 1)² .

27. 6. Determine o grau do polinômio P(x) =
(a – 1) x³ + (a + 1)x² – ax + a
7. Calcule o valor numérico de P(x) = –𝑥4 +
3x³ – x² – 4x + 1, para:
a) x = 0
b) x = 1
c) x = –1
d) x = i
e) x = – i

28. 8. Utilizando o teorema abaixo, encontre
as possíveis raízes da equação polinomial
2x4 + 5x3 – 11x2 – 20x + 12 = 0.
DIVISORES DO TERMO INDEPENDENTE.
DIVISORES DO PRIMEIRO TERMO.

29. Para confirmar se os valores que
encontramos são realmente a raiz da
equação polinomial, vamos substituir cada
valor no lugar do x da equação. Através do
cálculo algébrico, se o polinômio resultar
em zero, então o número substituído é,
realmente, a raiz da equação.

30. OPERAÇÕES
COM
POLINÔMIOS

31. ADIÇÃO E
SUBTRAÇÃO
O procedimento utilizado na
adição e subtração de
polinômios envolve técnicas de
redução de termos semelhantes,
jogo de sinal, operações
envolvendo sinais iguais e sinais
diferentes.

32. EXEMPLO:
Considere os polinômios –2x² + 5x – e
–3x³ + 2x – 1.
(–2x² + 5x – 2) + (–3x³ + 2x – 1)
–2x² + 5x – 2 – 3x³ + 2x – 1
–2x² + 7x – 3x³ – 3
–3x³ – 2x² + 7x – 3
adição

33. (–2x² + 5x – 2) – (–3x³ + 2x – 1)
–2x² + 5x – 2 + 3x³ – 2x + 1
–2x² + 3x – 1 + 3x³
3x³ – 2x² + 3x – 1
subtração

34. A multiplicação com polinômio (com dois ou
mais monômios) pode ser realizada de três
formas:
Multiplicação de monômio com polinômio.
Multiplicação de número natural com
polinômio.
Multiplicação de polinômio com polinômio
MULTIPLICAÇÃO DE
POLINÔMIOS

35. b) 3x . ( 5x2 + 3x – 1) =
15x³ + 9x² - 3x
EXEMPLOS:
c) 3 (2x2 + x + 5) =
6x² + 3x + 15
a) (7x5) . (-3x2) = −21𝑥7

36. d) (3x – 1) . (5x2 + 2)=
15x³ + 6x – 5x² - 2

37. DIVISÃO DE POLINÔMIOS
A operação de divisão é composta por dividendo,
divisor, quociente e resto, no caso da divisão de
polinômio por polinômio, considerando que cada
um deles seja formado por mais de um
monômio, iremos considerar a seguinte divisão:

38. a) 6x3 : 3x = 2x²
EXEMPLOS:
b) (12x3 + 9 – 4x) : (x + 2x2 + 3) =

39. TEOREMA DO RESTO
O resto da divisão de um
polinômio por um binômio do 1º
grau é o valor numérico que o
polinômio assume quando o “x” é
substituído pela raiz do divisor.

40. CALCULAA RAIZ DO BINÔMIO E
SUBSTITUI NO POLINÔMIO
O resto da divisão de P(x) = 2x² - x -1 por x - 1
X – 1 = 0
X = 1
RAIZ DO BINÔMIO
P(1) = 2 . 1² - 1 – 1
P(1) = 2 – 1 – 1
P(1) = 0 (resto)
A DIVISÃO É
EXATA
NOTA:
- O POLINÔMIO É
DIVISÍVEL PELO
BINÔMIO.
- A RAIZ DO BINÔMIO
TAMBÉM É RAIZ DO
POLINÔMIO.

41. Ex: qual é o valor de m para que a divisão do
polinômio P(x) = 2𝑥4 − 5𝑥3 + 𝑚𝑥2 + 3𝑥 −
2 por
D(x) = 𝑥 − 3 tenha resto igual a 88?
X – 3 = 0
X = 3
RAIZDOBINÔMIO
𝟐. 𝟑 𝟒
− 𝟓. 𝟑 𝟑
+ 𝒎. 𝟑 𝟐
+𝟑. 𝟑 − 𝟐 = 𝟖𝟖
2. 81 – 5.27 + m.9 + 9 – 2 = 88
162 – 135 + 9m + 9 – 2 = 88
9m + 27 + 7 = 88
9m = 88 – 27 – 7
9m = 54
m =
𝟓𝟒
𝟗
m = 6

42. Exemplo:
Sem efetuar as divisões,
prove que o polinômio
P(x) = x4 - 4x3 + 4x2 - 4x
+3 é divisível por x - 3

43. Dessa forma, basta aplicarmos o
Teorema do Resto.
Então:
P(x) = x4 - 4x3 + 4x2 - 4x +3
P(3) = 34 – 4 . 33 + 4 . 32 – 4 . 3 + 3
P(3) = -3 + 3
P(3) = 0
x – 3 = 0
x = 3