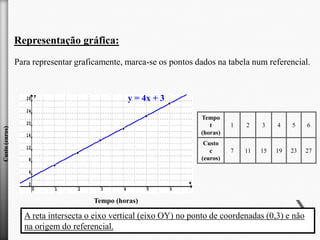
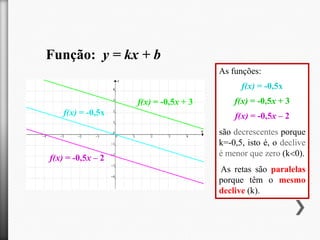
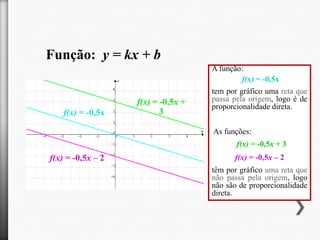
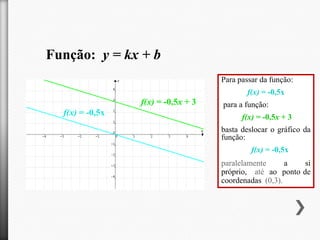
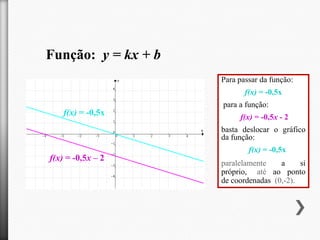
O documento descreve o aluguer de máquinas de limpeza de alcatifas pela empresa "Limpopó". A taxa de aluguer é de 4€ por hora mais 3€ de taxa fixa. Assim, quanto mais tempo a máquina é alugada, maior é o preço total, de acordo com a função afim f(x)=4x+3.

2. Exemplo:
A empresa “Limpopó” aluga máquinas para a limpeza de alcatifas. O aluguer de
cada máquina tem um preço, por hora, de 4€, acrescido de uma taxa fixa de 3€
, isto é, a partir do momento em que a pessoa aluga a máquina tem de pagar 3€.

3. Função: y = kx + b
1
Tempo
Preço
2
7
4+3
4 1+3
k
x
4
11
8+3
4
3
15
12 + 3
4 3+3
19
16 + 3
4 4+3
2+3
5
6
23
27
24 + 3
20 + 3
4 5+3 4 6+3
b
Em todos os casos, a primeira parcela varia com o tempo e a segunda é fixa (3€).

4. Qual é a expressão algébrica desta função?
f ( x)
Declive da reta
4x
3
ou
f ( x)
3 4x
Ordenada na origem
Uma função cuja expressão algébrica é do tipo y =kx +b (em que k e b são
números quaisquer) designa-se por função afim.

5. Representação gráfica:
Para representar graficamente, marca-se os pontos dados na tabela num referencial.
y = 4x + 3
1
2
3
4
5
6
Custo
c
(euros)
Custo (euros)
Tempo
t
(horas)
7
11
15
19
23
27
Tempo (horas)
A reta intersecta o eixo vertical (eixo OY) no ponto de coordenadas (0,3) e não
na origem do referencial.

6. Exemplo:
Considera as seguintes funções do tipo y = kx + b.
h(x) = 2x , i (x) = 2x + 3, j(x) = 2x - 5
- Num mesmo referencial, representa graficamente
as três funções.
- Qual é a posição relativa das retas que
representam as funções?
- Indica as coordenadas dos pontos de interseção
de cada uma das retas com o eixo das
ordenadas.
Conclusão:
- Funções afins cujas expressões algébricas tenham o mesmo declive são
representadas graficamente por retas paralelas.

7. Exemplo:
Conclusão:
- O gráfico de uma função afim y = kx + b é uma reta cuja representação gráfica
pode ser obtida a partir da deslocação da representação gráfica de y = kx
paralelamente a si própria para cima ou para baixo dependendo do sinal de b.

8. Qual é a influência da variação do parâmetros k e b na reta que
representa a função afim y=kx +b.
Parâmetro k : declive da reta

9. Nota:
- Qualquer ponto do eixo Ox (eixo das abcissas) tem ordenada zero.
Logo, as coordenadas são do tipo (x,0).
- Qualquer ponto do eixo Oy (eixo das ordenadas) tem abcissa zero.
Logo, as coordenadas são do tipo (0,y).

10. Exemplo:
Considera as seguintes funções do tipo y = kx + b.
h(x) = x + 3 , i(x) = -3x + 3, j(x) = 2x + 3
- Num mesmo referencial, representa graficamente
as três funções.
- Qual é a posição relativa das retas que
representam as funções?
- Indica as coordenadas dos pontos de interseção
de cada uma das retas com o eixo das ordenadas.
Conclusão:
As funções afins, y = kx + b, com a mesma ordenada na origem correspondem a
retas que têm um ponto comum: o ponto de coordenadas (0,b).

11. Qual é a influência da variação do parâmetros k e b na reta que
representa a função afim y=kx +b.
Parâmetro b : ordenada na origem
- O parâmetro b na expressão y = kx + b chama- se ordenada na origem e é a
ordenada do ponto de interseção da reta com o eixo das ordenadas.
- O gráfico da função y =kx + b é uma reta que interseta o eixo das ordenadas
no ponto de coordenadas ( 0, b).

12. Função: y = kx + b
f(x) = 2x
f(x) = 2x – 1
f(x) = 2x + 2
As funções:
f(x) = 2x
f(x) = 2x + 2
f(x) = 2x – 1
são crescentes porque k= 2,
isto é, o declive é maior
que zero ( k 0).
As retas são paralelas
porque têm o mesmo
declive (k).

13. Função: y = kx + b
f(x) = 2x
f(x) = 2x – 1
A função:
f(x) = 2x
tem por gráfico uma reta que
passa pela origem, logo é de
proporcionalidade direta.
f(x) = 2x + 2
As funções:
f(x) = 2x + 2
f(x) = 2x – 1
têm por gráfico uma reta que
não passa pela origem, logo
não são de proporcionalidade
direta.

14. Função: y = kx + b
f(x) = 2x
Para passar da função:
f(x) = 2x
para a função:
f(x) = 2x + 2
f(x) = 2x + 2
basta deslocar o gráfico da
função:
f(x) = 2x
paralelamente
a
si
próprio, até ao ponto de
coordenadas (0,2).

15. Função: y = kx + b
f(x) = 2x
Para passar da função:
f(x) = 2x – 1
f(x) = 2x
para a função:
f(x) = 2x -1
basta deslocar o gráfico da
função:
f(x) = 2x
paralelamente
a
si
próprio, até ao ponto de
coordenadas (0,-1).

16. Função: y = kx + b
f(x) = 2x + 2
A reta que define a
função:
f(x) = 2x + 2
intersecta o eixo das
ordenadas
(eixo
vertical) no ponto de
coordenadas (0,2), 2 é
a ordenada na origem.

17. Função: y = kx + b
f(x) = 2x – 1
A recta que define a
função:
f(x) = 2x - 1
intersecta o eixo das
ordenadas
(eixo
vertical) no ponto de
coordenadas (0,-1), -1
é a ordenada na
origem.

18. Função: y = kx + b
As funções:
f(x) = -0,5x
f(x) = -0,5x + 3
f(x) = -0,5x
f(x) = -0,5x – 2
f(x) = -0,5x + 3
f(x) = -0,5x – 2
são decrescentes porque
k=-0,5, isto é, o declive
é menor que zero (k 0).
As retas são paralelas
porque têm o mesmo
declive (k).

19. Função: y = kx + b
A função:
f(x) = -0,5x
f(x) = -0,5x
f(x) = -0,5x +
3
tem por gráfico uma reta que
passa pela origem, logo é de
proporcionalidade direta.
As funções:
f(x) = -0,5x + 3
f(x) = -0,5x – 2
f(x) = -0,5x – 2
têm por gráfico uma reta que
não passa pela origem, logo
não são de proporcionalidade
direta.

20. Função: y = kx + b
Para passar da função:
f(x) = -0,5x
f(x) = -0,5x + 3
f(x) = -0,5x
para a função:
f(x) = -0,5x + 3
basta deslocar o gráfico da
função:
f(x) = -0,5x
paralelamente
a
si
próprio, até ao ponto de
coordenadas (0,3).

21. Função: y = kx + b
Para passar da função:
f(x) = -0,5x
para a função:
f(x) = -0,5x
f(x) = -0,5x - 2
basta deslocar o gráfico
da função:
f(x) = -0,5x – 2
f(x) = -0,5x
paralelamente
a
si
próprio, até ao ponto
de coordenadas (0,-2).

22. Função: y = kx + b
A recta que define a
função:
f(x) = -0,5x + 3
f(x) = -0,5x + 3
intersecta o eixo das
ordenadas
(eixo
vertical) no ponto de
coordenadas (0,3), 3
é a ordenada na
origem.

23. Função: y = kx + b
A reta que define a
função:
f(x) = -0,5x - 2
f(x) = -0,5x – 2
intersecta o eixo das
ordenadas
(eixo
vertical) no ponto de
coordenadas (0,-2) e
-2 é a ordenada na
origem.

24. Gráficos das funções do tipo y = kx+b
- A representação gráfica duma função do tipo y = kx + b, com k e b constantes,
é uma reta que interseta o eixo das ordenadas em (0,b) e é paralela à reta que
representa a função y = kx.
- O gráfico da função y=kx+b sofre um deslocamento de b unidades, no eixo das
ordenadas, relativamente ao gráfico de y=kx, a função de proporcionalidade
direta.

25. Determinação do declive de uma reta

26. Função constante
Uma função definida por uma expressão algébrica do tipo
y= b, sendo b uma constante, é uma função constante.
O gráfico de uma função constante é uma reta paralela
ao eixo das abcissas que corta o eixo das ordenadas no
ponto (0, b).
Exemplo:

27. Nota:
- Uma função do tipo y = b, chama-se função constante porque qualquer que
seja o objeto, a sua imagem é sempre a mesma.
- Numa reta horizontal, que corresponde a uma função constante (y=b), o
declive é zero.

28. Casos particulares da função afim
- Todas as funções lineares (do tipo y = kx) são funções afins, em que b = 0.
Representa uma situação de proporcionalidade direta e tem por gráfico uma reta
que contém a origem do referencial.
- Todas as funções constantes (do tipo y = b) são funções afins, em que k = 0,
cujo gráfico é uma reta horizontal que contém o ponto (0,b).
-
O gráfico de uma função afim não linear e não constante é uma reta que não
passa pela origem do referencial e não é horizontal.