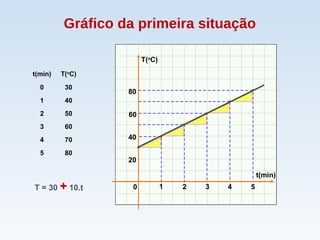
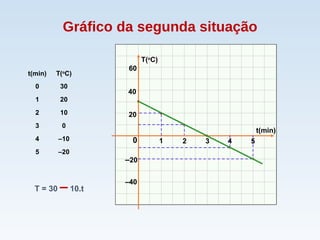
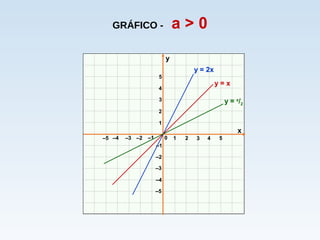
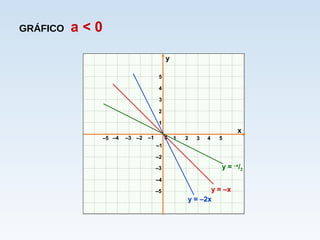
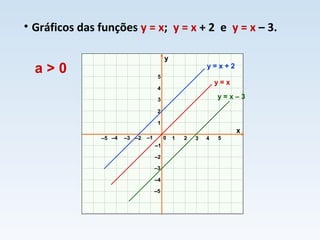
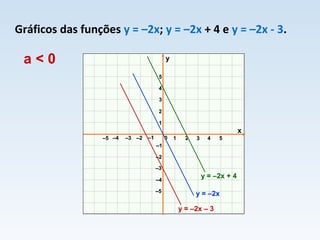
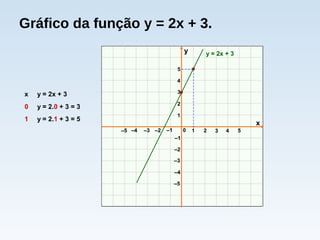
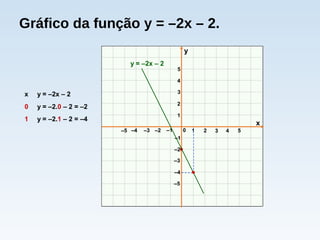
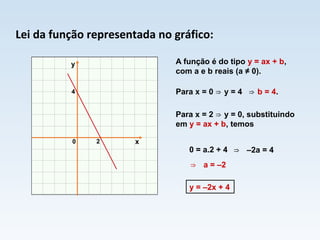
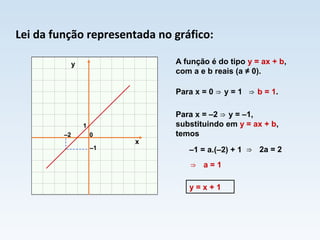
O documento descreve duas situações de variação de temperatura em função do tempo. Na primeira, a temperatura aumenta a uma taxa constante de 10°C por minuto, modelada pela função T = 30 + 10t. Na segunda, a temperatura diminui a uma taxa constante de 10°C por minuto, modelada pela função T = 30 - 10t. Ambas as situações são exemplos de funções afins.

1. Função afim: a
função polinomial
de 1º grau

2. Vamos analisar a variação
de temperatura de certa
substância em duas
situações distintas:

3. ① AUMENTANDO 10°C por minuto.
t(min) 0 1 2 3 4 5
T(o
C) 30 40 50 60 70 80
A temperatura da substância é medida minuto a minuto:
A taxa de variação da temperatura é positiva e constante = 10o
C/min
Após t minutos, a temperatura T da substância em o
C é,
T = 30 + 10.t

4. ② DIMINUINDO 10°C por minuto.
t(min) 0 1 2 3 4 5
T(o
C) 30 20 10 0 –10 – 20
Após t minutos, a temperatura T da substância em o
C é,
T = 30 – 10.t
A temperatura da substância é medida minuto a minuto:
A taxa de variação da temperatura é negativa e constante =
-10o
C/min

5. Gráfico da primeira situação
t(min) T(o
C)
0 30
1 40
2 50
3 60
4 70
5 80
t(min)
T(o
C)
0 1 2 3 4
20
40
60
80
5T = 30 + 10.t

6. Gráfico da segunda situação
t(min) T(o
C)
0 30
1 20
2 10
3 0
4 –10
5 –20
t(min)
T(o
C)
0 1 2 3 4
–20
–40
20
40
5
T = 30 – 10.t
60

7. Função afim ou polinomial de 1º grau é toda função do
tipo:
y = f(x) = ax + b
Em que a e b são constantes reais.
Situações cotidianas que envolvem
taxas de variação constante são
modeladas pela função afim.

8. CASOS PARTICULARES
FUNÇÃO f: R R
definida por
Coeficientes a
e b
Gráfico
LINEAR f(x)= ax a ≠ 0 e b = 0
CONSTANTE f(x) = b a = 0 e b ≠ 0
IDENTIDADE
f(x) = x a = 1 e b = 0

9. CRESCIMENTO E
DECRESCIMENTO.
a > 0 ⇒ função crescente
⇒ reta ascendente (sobe da esquerda p/ direita)
a < 0 ⇒ função decrescente
⇒ reta descendente (desce da esquerda p/ direita)

10. GRÁFICO - a > 0
x
y
0 1 2 3–3 –2 –1
1
2
3
–3
–2
–1
4 5–4–5
–5
–4
4
5
y = x
y = x
/2
y = 2x

11. x
y
0 1 2 3–3 –2 –1
1
2
3
–3
–2
–1
4 5–4–5
–5
–4
4
5
y = –x
y = –x
/2
y = –2x
a < 0GRÁFICO

12. A partir do gráfico da função linear y =
ax obtemos os gráficos de todas as
funções afins y = ax + b, deslocando o
gráfico para cima ou para baixo de
acordo com o valor da constante b

13. • Gráficos das funções y = x; y = x + 2 e y = x – 3.
x
y
0 1 2 3–3 –2 –1
1
2
3
–3
–2
–1
4 5–4–5
–5
–4
4
5
y = x
a > 0
y = x – 3
y = x + 2

14. Gráficos das funções y = –2x; y = –2x + 4 e y = –2x - 3.
x
y
0 1 2 3–3 –2 –1
1
2
3
–3
–2
–1
4 5–4–5
–5
–4
4
5
y = –2x + 4
y = –2x
a < 0
y = –2x – 3

15. A análise das duas últimas figuras sugere um caso
geral em relação a todas as funções afins do tipo y =
f(x) = ax + b.
• Que relação existe entre o coeficiente b e o
ponto onde cada reta corta o eixo y?
b é a ordenada do ponto em que a reta
corta o eixo y. Ou seja, a reta intercepta o
eixo y no ponto de coordenadas (0, b).

16. Gráfico da função y = 2x + 3.
x y = 2x + 3
0 y = 2.0 + 3 = 3
1 y = 2.1 + 3 = 5
x
y
0 1 2 3–3 –2 –1
1
2
3
–3
–2
–1
4 5–4–5
–5
–4
4
5
y = 2x + 3

17. Gráfico da função y = –2x – 2.
x y = –2x – 2
0 y = –2.0 – 2 = –2
1 y = –2.1 – 2 = –4
x
y
0 1 2 3–3 –2 –1
1
2
3
–3
–2
–1
4 5–4–5
–5
–4
4
5
y = –2x – 2

18. Nos gráficos das funções de 1º grau, a reta
sempre corta o eixo x. A abscissa do ponto
por onde o gráfico da função intercepta esse
eixo é chamada de zero ou raiz da função.
Raiz da função é o valor de x tais que f(x) = 0.

19. Lei da função representada no gráfico:
x
y
0 2
4
A função é do tipo y = ax + b,
com a e b reais (a ≠ 0).
Para x = 0 y = 4⇒
Para x = 2 y = 0, substituindo⇒
em y = ax + b, temos
0 = a.2 + 4 –⇒ 2a = 4
⇒ a = –2
y = –2x + 4
⇒ b = 4.

20. A função é do tipo y = ax + b,
com a e b reais (a ≠ 0).
Para x = 0 y = 1⇒
Para x = –2 y = –1,⇒
substituindo em y = ax + b,
temos
–1 = a.(–2) + 1 ⇒ 2a = 2
⇒ a = 1
y = x + 1
⇒ b = 1.
x
y
0–2
1
–1
Lei da função representada no gráfico: