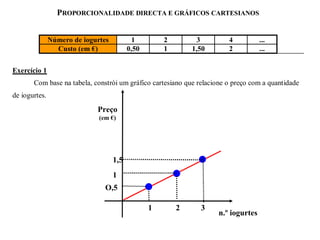
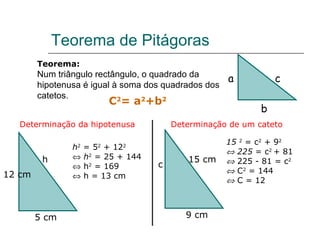
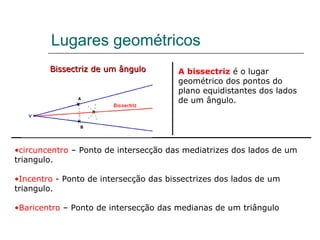
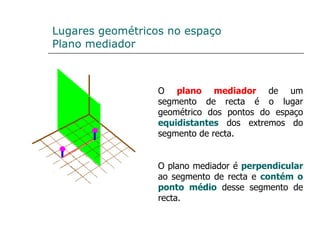
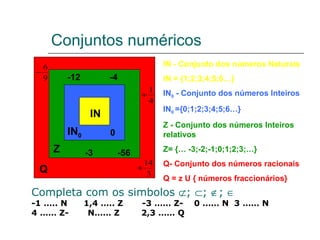
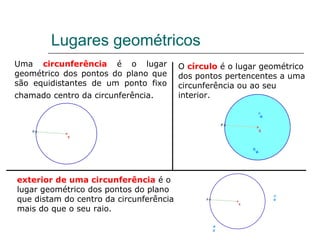
1) O documento resume os principais conteúdos de Matemática do 7o e 8o ano, incluindo teorema de Pitágoras, funções, semelhança de triângulos e estatística. 2) Fornece detalhes sobre como aplicar o teorema de Pitágoras e os critérios de semelhança de triângulos na resolução de problemas. 3) Discutem conceitos como múltiplos e divisores, potências, notação científica, lugares geométricos e medidas estatísticas.

1. Preparação para o teste intermédio de Matemática 8º ano Conteúdos do 7º ano Conteúdos do 8º ano

2. Conteúdos do 8º Ano Teorema de Pitágoras Funções Semelhança de triângulos Ainda os números Lugares geométricos Estatística

3. Conteúdos do 7º Ano Do Espaço ao Plano Semelhança de Figuras ( está abordado nos conteúdos do 8º ano) Conhecer melhor os números Conjuntos e operações Equações Proporcionalidade directa Estatística (está abordado nos conteúdos do 8º ano)

4. Teorema de Pitágoras Teorema: Num triângulo rectângulo, o quadrado da hipotenusa é igual à soma dos quadrados dos catetos. a b c C 2 = a 2 +b 2 Determinação da hipotenusa h 2 = 5 2 + 12 2  h 2 = 25 + 144  h 2 = 169  h = 13 cm 15 2 = c 2 + 9 2  225 = c 2 + 81  225 - 81 = c 2  C 2 = 144  C = 12 Determinação de um cateto 9 cm 5 cm 12 cm c 15 cm h

5. Semelhança de triângulos Critérios de semelhança de triângulos Dois triângulos são semelhantes se: Tiverem dois ângulos geometricamente iguais Tiverem os três lados correspondentes directamente proporcionais Tiverem dois lados directamente proporcionais e o ângulo por eles formado for igual

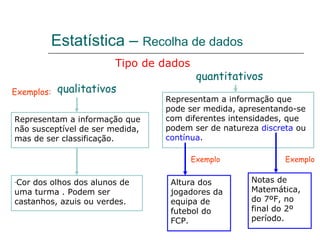
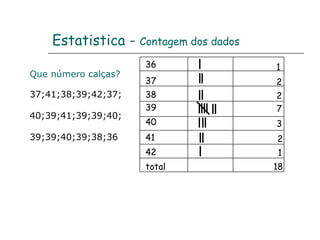
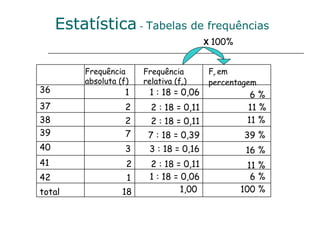
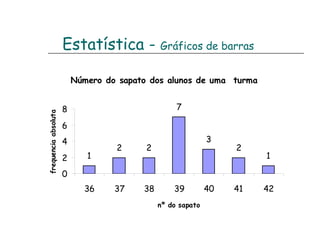
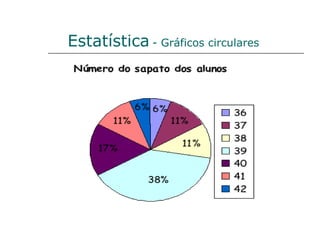
6. Escola EB 2,3 Prof. Dr. Egas Moniz - Avanca Aplicação dos critérios de semelhança de triângulos 1. Determina a altura da árvore. Serão os triângulos [ABE] e [CDE] semelhantes? Sim, porque tem dois ângulos geometricamente iguais, o de 90º e o ângulo AEB. Determinação da altura da árvore. 5,2 = h  h = 5,2 x 0,8 : 1,6 1,6 0,8 h = 5,2 x 0,8 : 1,6 h = 2,6 m A altura da árvore é de 2,6 metros. 3,6 + 1,6 = 5,2 m Semelhança de triângulos

7. Semelhança de triângulos Relação entre perímetros e áreas de figuras semelhantes Se dois polígonos A e B são semelhantes e a razão de semelhança de A para B é r, então: A razão entre os perímetros de A e B é r. A Razão entre as áreas de A e B é r2. P B :P A = r A B :A A =r 2

8. Funções Definição : Uma função é uma correspondência entre A e B que a cada elemento de A faz corresponder um e um só elemento de B Formas de definir uma função: Por um diagrama Por uma tabela Por uma expressão analítica Por um gráfico

9. Funções definidas por um diagrama Ex. Não são funções Ex. Funções 1 2 3 4 -1 -2 -3 1 2 -1 2 1 2 3 -1 -7 -2 -4 -3 A B D f = {1;2,3} D’ f = {-1;-2,-3} Objectos: 1;2,3 Imagens: -1;-2;-3 A – Conjunto de Partida B – Conjunto de chegada f ( 2 ) = -2 f ( x ) = -x f

10. Funções definidas por uma Tabela D f = {1;2,3;4} D’ f = {4;8;12;16} Objectos: 1;2,3;4 Imagens: 4;8;12;16 Variável independente: Lado do quadrado Variável dependente: Perímetro do quadrado f ( 2 ) = 8 f ( x ) = 4x Seja a função f definida pela tabela seguinte 16 12 8 4 Perímetro do quadrado (P) 4 3 2 1 Lado de um quadrado (L)

11. Funções definidas por uma expressão analítica Seja a função f definida pela seguinte expressão analítica f(x ) = 2x -1 Calcular a imagem sendo dado o objecto f(3) = 2 x 3 -1 f(3) = 5 Calcular o objecto sendo dada a imagem f(x) = 15  2x – 1 = 15  2x = 15 + 1  2x = 16  x = 8 (3;5) e (8;15) pertencem à recta que é gráfico da função f.

12. Funções definidas por um gráfico Variável independente: Peso Variável dependente: Custo F( … ) = 12 F(1) = ….. Tipo de função: Linear Expressão analítica: f(x) = 6x

13. Ainda os Números Múltiplos e divisores Potências Notação cientifica

14. Múltiplos e divisores ( m.m.c) 1º processo M 12 = {0;12;24;36;48;60…} M 30 = {0;30;60…} m.m.c = {60} Determina o m.m.c(12;30) 2º processo 12 2 30 2 6 2 15 3 3 3 5 5 1 1 12 = 2 2 x 3 30 = 2 x 3 x 5 m.m.c = 2 2 x 3 x5 = 60 Produto dos factores primos comuns e não comuns elevados ao maior expoente

15. Múltiplos e divisores ( M.d.c) 1º processo D 12 = {1;2;3;4;6;12} D 30 = {1;2;3;5;6;10;15;30} M.d.c = {6} Determina o m.d.c(12;30) 2º processo 12 2 30 2 6 2 15 3 3 3 5 5 1 1 12 = 2 2 x 3 30 = 2 x 3 x 5 M.d.c = 2 x 3 = 6 Produto dos factores primos comuns elevados ao menor expoente

16. Potências Regras operatórias das potências Multiplicação Com a mesma base 2- 2 x 2 7 = 2 5 Com o mesmo expoente (-2) 3 x (-7) 3 = 14 3 Divisão Com a mesma base 2 -2 : 2 7 = 2 -9 = Com o mesmo expoente (-24) 3 : (-6) 3 = 4 3 Potencia de potência (2 3 ) 5 = 2 15 Potencia de expoente inteiro negativo 5 -1 = 1 5 Potencia de expoente nulo 5 0 = 1

17. Notação Científica Definição : Diz-se que um número está escrito em notação cientifica se está escrito na forma de um produto de um número a entre 1 e 10 e uma potência de base 10, e escreve-se: a x 10 n , com 1≤a<10 Ex: Escreve os seguintes números em notação cientifica 253 x 10 -3 6769800 0,0000008 76,9 x 10 5 Operações com números escritos em notação científica Multiplicação (2,1 x 10 -3 ) x (2 x10 8 ) = (2,1 x2) x (10 -3 x 10 8 ) = 4,2 x 10 5 Divisão (8,04 x 10 -7 ) : ( 4,02 x 10 5 ) = 2,02 x 10 -12

18. Lugares geométricos Uma circunferência é o lugar geométrico dos pontos do plano que são equidistantes de um ponto fixo chamado centro da circunferência. O círculo é o lugar geométrico dos pontos pertencentes a uma circunferência ou ao seu interior. exterior de uma circunferência é o lugar geométrico dos pontos do plano que distam do centro da circunferência mais do que o seu raio.

19. Lugares geométricos Coroa circular: É o conjunto dos pontos do plano que se encontram a uma distancia de C maior ou igual a r 1 e menor ou igual a r 2. r 1 r 2 Mediatriz de um segmento de recta, [AB] É o lugar geométrico dos pontos do plano equidistantes dos extremos do segmento de recta, [AB]

20. Lugares geométricos Bissectriz de um ângulo A bissectriz é o lugar geométrico dos pontos do plano equidistantes dos lados de um ângulo. circuncentro – Ponto de intersecção das mediatrizes dos lados de um triangulo. Incentro - Ponto de intersecção das bissectrizes dos lados de um triangulo. Baricentro – Ponto de intersecção das medianas de um triângulo

21. Lugares geométricos no espaço Superfície esférica e esfera Ao lugar geométrico dos pontos do espaço equidistantes de um ponto fixo chamado centro, dá-se o nome de superfície esférica . A esfera é o lugar geométrico de todos os pontos do espaço que se encontram a igual ou menor distância de um ponto fixo chamado centro.

22. Lugares geométricos no espaço Plano mediador O plano mediador de um segmento de recta é o lugar geométrico dos pontos do espaço equidistantes dos extremos do segmento de recta. O plano mediador é perpendicular ao segmento de recta e contém o ponto médio desse segmento de recta.

23. Estatística Recolha de dados Tabelas de frequências Gráficos Medidas de tendência CENTRAL

24. qualitativos Representam a informação que não susceptível de ser medida, mas de ser classificação. Exemplos: Cor dos olhos dos alunos de uma turma . Podem ser castanhos, azuis ou verdes. Representam a informação que pode ser medida, apresentando-se com diferentes intensidades, que podem ser de natureza discreta ou contínua . Exemplo quantitativos Notas de Matemática, do 7ºF, no final do 2º período. Exemplo Altura dos jogadores da equipa de futebol do FCP. Estatística – Recolha de dados Tipo de dados

25. Estatistica - Contagem dos dados 36 37 38 39 40 total 1 2 2 7 3 18 41 42 2 1 Que número calças? 37;41;38;39;42;37; 40;39;41;39;39;40; 39;39;40;39;38;36

26. Frequência absoluta (f) Frequência relativa (f r ) F r em percentagem 6 % 11 % 11 % 39 % 16 % 11 % X 100% 1 : 18 = 0,06 2 : 18 = 0,11 2 : 18 = 0,11 7 : 18 = 0,39 3 : 18 = 0,16 1,00 36 37 38 39 40 total 41 42 1 2 2 7 3 18 2 1 2 : 18 = 0,11 1 : 18 = 0,06 6 % 100 % Estatística - Tabelas de frequências

27. Estatística - Gráficos de barras

28. Pictograma = 1 aluno Estatística - Pictograma

29. Estatística - Gráficos circulares Frequência absoluta (f) Graus 20º 40º 40º 140º 60º 360º 36 37 38 39 40 total 41 42 1 2 2 7 3 18 2 1 40º 20º

30. Estatística - Gráficos circulares

31. Estatística – Medidas de tendência central Média A média do número do sapato dos alunos é 39,1 1 36 2 37 Frequência absoluta (f) 18 1 2 3 7 2 Total 42 41 40 39 38

32. Estatística – Medidas de tendência central Moda - É o valor que surge com mais frequência se os dados são discretos. Neste caso a moda é 39. Mediana - Ordenados os elementos, a mediana é o valor que a divide ao meio, isto é, 50% dos elementos da amostra são menores ou iguais à mediana e os outros 50% são maiores ou iguais à mediana. 36;37;37;38;38;39;39;39;39;39;39;39;40;40;40;41;41;42 (39 + 39) : 2 = 39 1 36 2 37 Frequência absoluta (f) 18 1 2 3 7 2 Total 42 41 40 39 38

33. EQUAÇÃO : é uma igualdade entre duas expressões onde, pelo menos numa delas, figura uma ou mais letras . Equações 3x+5=2-x+4 Sou equação 3+(5-2-4) = 3+1 Não sou equação 1º membro 2º membro termos: ; -2 ; 3 x ; - 4 ; - x incógnita: x termos com incógnita: 3 x ; - x ; termos independentes: -2 ; -4

34. Solução de uma equação : é um número que colocado no lugar da incógnita transforma a equação numa igualdade numérica verdadeira SOLUÇÃO Equações 6 5 SOLUÇÃO 5 SOLUÇÃO Equações equivalentes: Mesmo conjunto solução

35. Resolver uma equação é determinar a sua solução. Equações sem parênteses e sem denominadores efectuamos as operações. Dividimos ambos os membros pelo coeficiente da incógnita . Conjunto solução Determinamos a solução. Numa equação podemos mudar termos de um membro para o outro , desde que lhes troquemos o sinal Num dos membros ficam os termos com incógnita e no outro os termos independentes

36. EQUAÇÕES COM PARÊNTESES simplificação de expressões com parênteses: Sinal menos antes dos parênteses : Tiramos os parênteses trocando os sinais dos termos que estão dentro Sinal mais antes dos parênteses: Tiramos os parênteses mantendo os sinais que estão dentro. Número antes dos parênteses: Tiramos os parênteses, aplicando a propriedade distributiva.

37. Como resolver uma equação com parênteses. Eliminar parênteses. Agrupar os termos com incógnita. Efectuar as operações Dividir ambos os membros pelo coeficiente da incógnita Determinar a solução, de forma simplificada. C.S =

38. EQUAÇÕES COM DENOMINADORES Começamos por reduzir todos os termos ao mesmo denominador. Duas fracções com o mesmo denominador são iguais se os numeradores forem iguais. Podemos tirar os denominadores desde que sejam todos iguais.

39. Esta fracção pode ser apresentada da seguinte forma Sinal menos antes de uma fracção O sinal menos que se encontra antes da fracção afecta todos os termos do numerador. 1 (2) (6) (3) (3) Começamos por “desdobrar” a fracção que tem o sinal menos antes.(atenção aos sinais!) Reduzimos ao mesmo denominador e eliminamos os denominadores.

40. EQUAÇÕES COM PARÊNTESES E DENOMINADORES Devemos começar por eliminar os parênteses e depois os denominadores (3) (3) (3) (2) (2) C.S.=

41. Proporcionalidade directa Razão

43. 0,5 0,5 0,5 0,5 0,5 0,5

45. Preço (em €) n.º iogurtes 1 2 3 O,5 1 1,5

46. Percentagens 5 % de 120 chocolates são _______ 0,05 x 120 = 6 6 chocolates em 50 são ___% 50------- 100% x = 6 x 100 : 50 6 -------- x 150 acrescidos de 10% são ____ 150 + 10% = 150 +15 = 165 500 com um desconto de 20% ____ 500 - 20% = 500-100 = 400

47. Resolução de problemas envolvendo Percentagens 1- O preço de um sofá é de 300€, sem IVA. Sabendo que o IVA é 21%, quanto é o valor, em euros, do IVA deste sofá? Qual é o preço final do sofá? 21% de 300 = 300 x 21% = 63 300 + 63 = 363 O preço final do sofá é 363 euros. 2- Uma camisola custava 56 euros e a Ana que era amiga da dona da loja, comprou-a por 42 euros. Qual foi a percentagem de desconto? Euros % 56 -------------------------- 100 42 --------------------------- x x = 42 x 100 : 56 = 75% 100 – 75 % = 25 % O desconto foi de 25%.

48. Conjuntos numéricos IN - Conjunto dos números Naturais IN = {1;2;3;4;5;6…} IN 0 - Conjunto dos números Inteiros IN 0 ={0;1;2;3;4;5;6…} Z - Conjunto dos números Inteiros relativos Z= {… -3;-2;-1;0;1;2;3;…} Q- Conjunto dos números racionais Q = z U { números fraccionários} Completa com os simbolos  ;  ;  ;  -1 ….. N 1,4 ….. Z -3 …… Z- 0 …… N 3 …… N 4 …… Z- N…… Z 2,3 …… Q IN Q Z IN 0 -3 -56 -12 -4 0