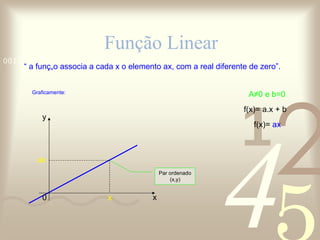
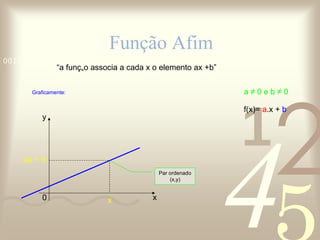
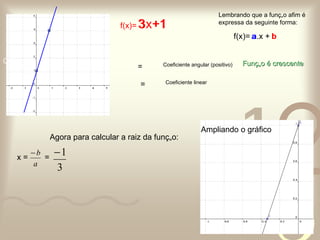
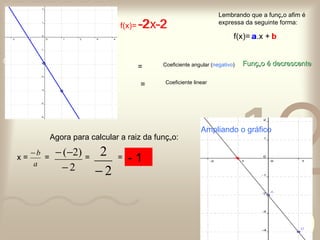
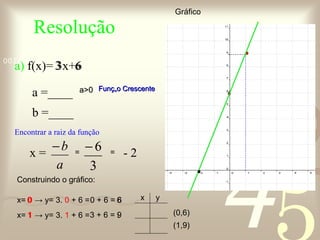
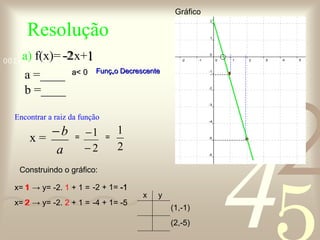
O documento discute conceitos de funções matemáticas, incluindo: 1) A importância das funções para compreender relações entre fenômenos; 2) Definições e exemplos de funções do 1o e 2o grau, como funções constantes, identidade, lineares e afins; 3) Como representar graficamente essas funções e encontrar suas raízes.