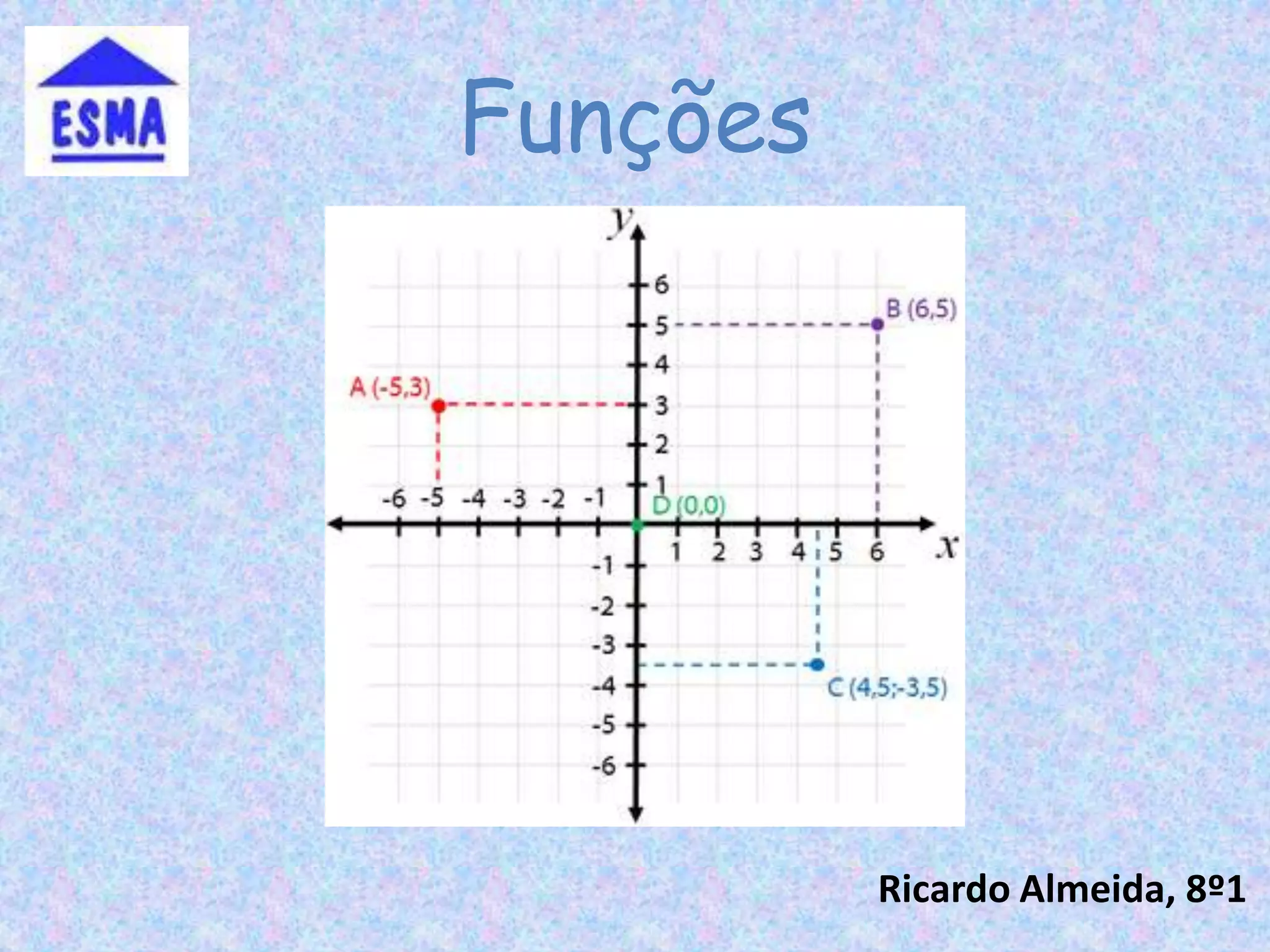
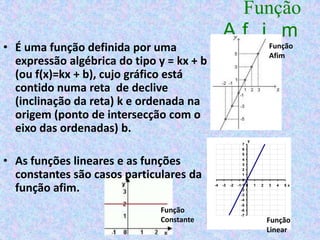
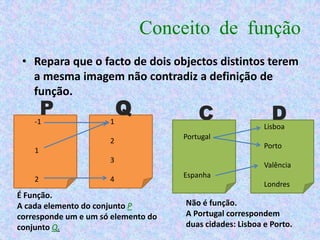
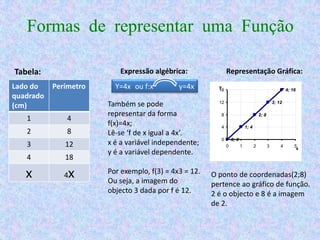
1) O documento descreve os conceitos de função, referencial cartesiano, domínio, contradomínio e diferentes tipos de funções como funções constantes, afins, de proporcionalidade e suas representações gráficas. 2) Uma função é uma correspondência entre dois conjuntos onde cada elemento do primeiro conjunto está associado a um único elemento do segundo. 3) Existem diferentes formas de representar funções incluindo tabelas, expressões algébricas e gráficos.

1. Funções
Ricardo Almeida, 8º1

2. Re f e r e n c i a
l
• Um referencial C a r t e s i a n o
cartesiano é constituido
por dois eixos orientados,
perpendiculares entre si,
que se intersectam num
ponto a que se chama
origem do referencial e,
normalmente,
representa-se por O.

3. Conceito de função
• Uma função é uma correspondência entre dois
conjuntos que a cada elemento do primeiro
conjunto associa um e um só elemento do segundo
conjunto (correspondência unívoca).

4. Conceito de função
• Repara que o facto de dois objectos distintos terem
a mesma imagem não contradiz a definição de
função.
-1
P 1
Q C D
Lisboa
Portugal
2
Porto
1
3
Valência
Espanha
2 4
Londres
É Função.
A cada elemento do conjunto P Não é função.
corresponde um e um só elemento do A Portugal correspondem
conjunto Q. duas cidades: Lisboa e Porto.

5. Domínio e contradomínio de
uma função
• Numa função, o domínio é o conjunto dos objectos.
• Contradomínio é o conjunto das suas imagens.
P Q
1
-1
D={-1;1;2}
D`={1;4}
2
1 Conjunto de Chegada:
3 {1;2;3;4}
2
4
A cada elemento do conjunto P corresponde
um e um só elemento do conjunto Q

6. Formas de representar uma Função
Tabela: Expressão algébrica: Representação Gráfica:
Lado do Perímetro Y=4x ou f:x y=4x y
16 4; 16
quadrado
(cm) Também se pode 12 3; 12
representar da forma 8 2; 8
1 4
f(x)=4x; 4 1; 4
2 8 Lê-se ‘f de x igual a 4x’.
0 0; 0
3 12 x é a variável independente; 0 1 2 3 4 5
x
y é a variável dependente.
4 18
x 4x Por exemplo, f(3) = 4x3 = 12.
Ou seja, a imagem do
O ponto de coordenadas(2;8)
pertence ao gráfico de função.
objecto 3 dada por f é 12. 2 é o objecto e 8 é a imagem
de 2.

7. Função
Af i m
• É uma função definida por uma Função
Afim
expressão algébrica do tipo y = kx + b
(ou f(x)=kx + b), cujo gráfico está
contido numa reta de declive
(inclinação da reta) k e ordenada na
origem (ponto de intersecção com o
eixo das ordenadas) b.
y
7
6
5
• As funções lineares e as funções 4
3
2
constantes são casos particulares da 1
0
função afim. -4 -3 -2 -1-1 0
-2
-3
1 2 3 4 5x
-4
-5
Função -6
-7
Constante Função
Linear

8. Função d e
p r o p o r c i o n a l i d a d e
Uma função definidaa uma expressão
d i r e c t por
algébrica do tipo y = kx (ou f(x) = kx), k  0,
tem o nome de função de proporcionalidade
directa ou função linear.
x é um objecto;
y = f(x) é sua imagem;
k é a constante de proporcionalidade.
Uma função de proporcionalidade directa ou
uma função linear é uma função cujo gráfico
está contido numa reta que passa na origem.

9. Função
c o n s t a n t
Uma função definida por uma expressão e
algébrica do tipo y = k (ou f(x) = k) sendo k uma
constante, é uma função constante.
O gráfico de uma função constante está
contido numa reta paralela ao eixo Ox, ou seja,
horizontal.