Baixado 272 vezes
Carregado porRodrigo Carvalho
âNgulos
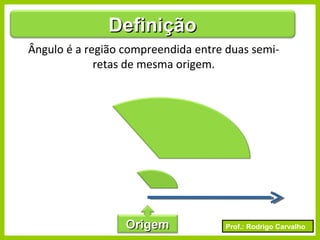
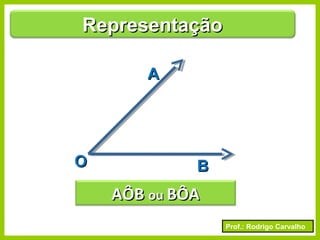
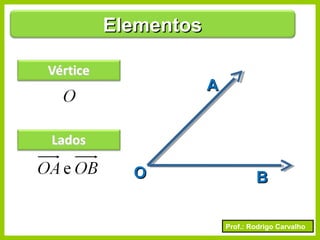
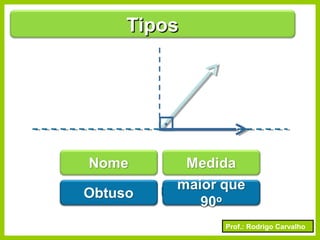
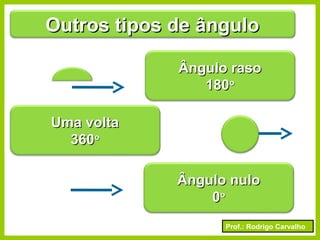
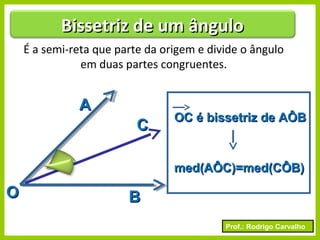
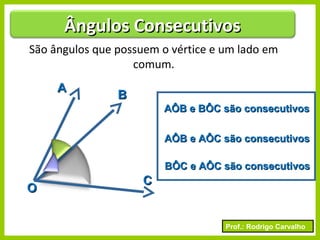
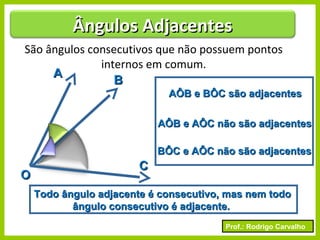
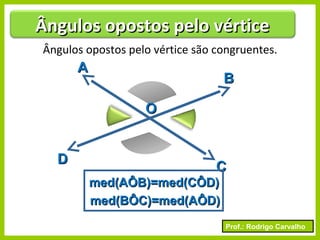
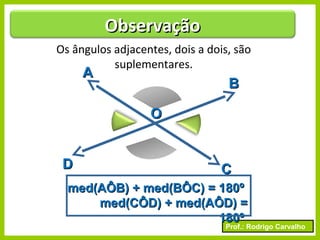
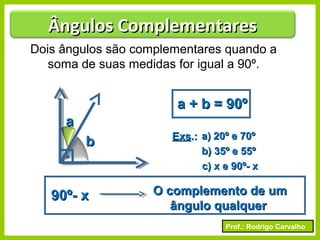
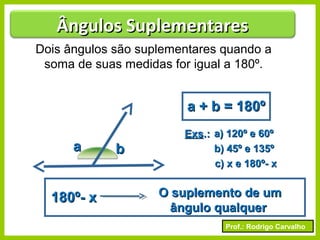
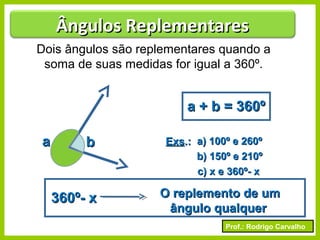
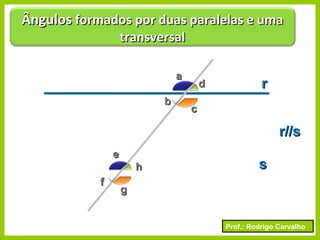
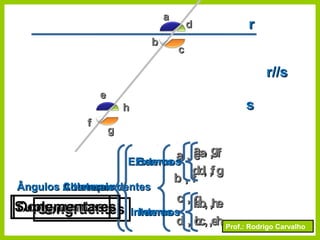
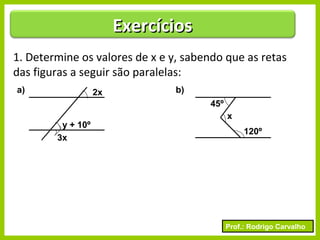
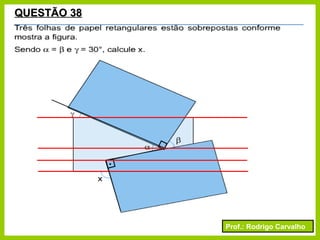
O documento apresenta conceitos básicos sobre ângulos, incluindo sua definição, tipos, elementos e relações entre ângulos como adjacentes, opostos e complementares. É apresentada a representação de ângulos e exemplos de cálculos envolvendo medidas de ângulos.
Mais conteúdo relacionado
âNgulos
- 1.
- 2. Prof.: Rodrigo Carvalho Ânguloé a região compreendida entre duas semi- retas de mesma origem. OrigemOrigem DefiniçãoDefinição
- 3.
- 4.
- 5. Prof.: Rodrigo Carvalho TiposTipos AgudoAgudo menorquemenor que 9090oo .
- 6. Prof.: Rodrigo Carvalho Outrostipos de ânguloOutros tipos de ângulo Uma voltaUma volta 360360oo Ângulo rasoÂngulo raso 180180oo Ângulo nuloÂngulo nulo 00oo
- 7. Prof.: Rodrigo Carvalho Éa semi-reta que parte da origem e divide o ângulo em duas partes congruentes. OO AA BB CC OC é bissetriz de AÔBOC é bissetriz de AÔB med(AÔC)=med(CÔB)med(AÔC)=med(CÔB) Bissetriz de um ânguloBissetriz de um ângulo
- 8. Prof.: Rodrigo Carvalho Sãoângulos que possuem o vértice e um lado em comum. AA OO BB CC AÔB e BÔC são consecutivosAÔB e BÔC são consecutivos AÔB e AÔC são consecutivosAÔB e AÔC são consecutivos BÔC e AÔC são consecutivosBÔC e AÔC são consecutivos Ângulos ConsecutivosÂngulos Consecutivos
- 9. Prof.: Rodrigo Carvalho Sãoângulos consecutivos que não possuem pontos internos em comum. AA BB CC OO AÔB e BÔC são adjacentesAÔB e BÔC são adjacentes AÔB e AÔC não são adjacentesAÔB e AÔC não são adjacentes BÔC e AÔC não são adjacentesBÔC e AÔC não são adjacentes Todo ângulo adjacente é consecutivo, mas nem todoTodo ângulo adjacente é consecutivo, mas nem todo ângulo consecutivo é adjacente.ângulo consecutivo é adjacente. Ângulos AdjacentesÂngulos Adjacentes
- 10. Prof.: Rodrigo Carvalho AA DD CC BB OO med(BÔC)=med(AÔD)med(BÔC)=med(AÔD) Ângulosopostos pelo vértice são congruentes. med(AÔB)=med(CÔD)med(AÔB)=med(CÔD) Ângulos opostos pelo vérticeÂngulos opostos pelo vértice
- 11. Prof.: Rodrigo Carvalho AA DDCC BB OO Os ângulos adjacentes, dois a dois, são suplementares. med(AÔB) + med(BÔC) = 180ºmed(AÔB) + med(BÔC) = 180º med(CÔD) + med(AÔD) =med(CÔD) + med(AÔD) = 180º180º ObservaçãoObservação
- 12. Prof.: Rodrigo Carvalho Doisângulos são complementares quando a soma de suas medidas for igual a 90º. . aa bb a + b = 90ºa + b = 90º a) 20º e 70ºa) 20º e 70ºExsExs.:.: b) 35º e 55ºb) 35º e 55º c) x e 90º- xc) x e 90º- x 90º- x90º- x O complemento de umO complemento de um ângulo qualquerângulo qualquer Ângulos ComplementaresÂngulos Complementares
- 13. Prof.: Rodrigo Carvalho Doisângulos são suplementares quando a soma de suas medidas for igual a 180º. aa bb a + b = 180ºa + b = 180º ExsExs.:.: a) 120º e 60ºa) 120º e 60º b) 45º e 135ºb) 45º e 135º c) x e 180º- xc) x e 180º- x 180º- x180º- x O suplemento de umO suplemento de um ângulo qualquerângulo qualquer Ângulos SuplementaresÂngulos Suplementares
- 14. Prof.: Rodrigo Carvalho ÂngulosReplementaresÂngulos Replementares Dois ângulos são replementares quando a soma de suas medidas for igual a 360º. a + b = 360ºa + b = 360º ExsExs.:.: a) 100º e 260ºa) 100º e 260º b) 150º e 210ºb) 150º e 210º c) x e 360º- xc) x e 360º- x 360º- x360º- x O replemento de umO replemento de um ângulo qualquerângulo qualquer aa bb
- 15. Prof.: Rodrigo Carvalho -O dobro do complemento de um ângulo:- O dobro do complemento de um ângulo: 2.(902.(90ºº - x)- x) - O complemento do dobro de um ângulo:- O complemento do dobro de um ângulo: 9090ºº - 2x- 2x - A metade do suplemento de um ângulo:- A metade do suplemento de um ângulo: 180180ºº - x- x 22 - O suplemento da metade de um ângulo:- O suplemento da metade de um ângulo: 180180ºº -- - O suplemento do complementoO suplemento do complemento de um ângulo:de um ângulo: 180180ºº - (90- (90ºº - x)- x) ObservaçõesObservações xx 22
- 16. Prof.: Rodrigo Carvalho 1.O triplo do complemento de um ângulo é igual ao suplemento da metade deste mesmo ângulo. Determine a medida do ângulo em questão. 2. A razão entre as medidas de dois ângulos complementares é igual a 2/3. Determine as medidas destes ângulos. ExercíciosExercícios
- 17. Prof.: Rodrigo Carvalho ÂngulosÂngulosformados por duas paralelas e umaformados por duas paralelas e uma transversaltransversal rr ss r//sr//s dd bb cc aa ff hh ee gg
- 18. Prof.: Rodrigo Carvalho rr ss r//sr//s dd bb cc aa ff hh ee gg ÂngulosCorrespondentesÂngulos Correspondentes a , ea , e b , fb , f c , gc , g d , hd , h CongruentesCongruentes Ângulos AlternosÂngulos Alternos ExternosExternos InternosInternos a , ga , g d , fd , f b , hb , h c , ec , e CongruentesCongruentes Ângulos ColateraisÂngulos Colaterais ExternosExternos InternosInternos a , fa , f d , gd , g b , eb , e c , hc , h SuplementaresSuplementares
- 19. Prof.: Rodrigo Carvalho ExercíciosExercícios 1.Determine os valores de x e y, sabendo que as retas das figuras a seguir são paralelas: 2x 3x y + 10º a) b) x 120º 45º
- 20. Prof.: Rodrigo Carvalho QUESTÃO38QUESTÃO 38 .
- 21. Prof.: Rodrigo Carvalho Sugestãode exercícios: LIVRO 2 - CAPÍTULO 01 Questões: 01, 02, 04, 06, 07, 10, 11, 14, 18, 21, 25, 28 e 29.