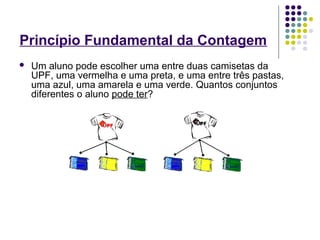
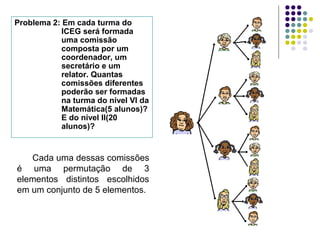
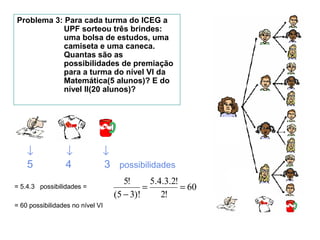
O documento discute os conceitos fundamentais da análise combinatória, incluindo permutações, arranjos, combinações e seus usos para resolver problemas de contagem. É apresentada a definição formal de cada conceito juntamente com exemplos numéricos de sua aplicação.

1. Análise Combinatória

2.  O que é análise combinatória?

3.  Análise Combinatória ou simplesmente
Combinatória, é o ramo da Matemática que
estuda os problemas relacionados a
contagem, ou seja, analisa coleções de
objetos que satisfaçam critérios ou atributos
específicos relacionados a contagem de
objetos nessas coleções.
Análise Combinatória

4.  Combinações de roupas
 Placas de automóveis
 Números de telefones
 Competições
 Premiações
 Formação de grupos, comissões
 Cardápios
 Rotas e caminhos
Análise Combinatória:
Situações cotidianas

5. Problemas de Contagem
 Um número de RG é composto por 10 algarismos, onde
o(s) primeiro(s) algarismo(s) pode(m) ser zero. Quantos
números de identidade são possíveis?

6. Problemas de Contagem
 Um número de RG é composto por 10 algarismos, onde
o(s) primeiro(s) algarismo(s) pode(m) ser zero. Quantos
números de identidade são possíveis?
= 10 possibilidades
= 10.000.000.000 identidades
10

7. Problemas de Contagem
 As placas de Licença de carros no Brasil consistem em sete
elementos: os três primeiros são letras(A – Z) e os quatro
últimos são números(0 – 9). Quantas placas de licença são
possíveis?

8. Problemas de Contagem
 As placas de Licença de carros no Brasil consistem em sete
elementos: os três primeiros são letras(A – Z) e os quatro
últimos são números(0 – 9). Quantas placas de licença são
possíveis?
= 26.26.26.10.10.10.10 possibilidades
= 175.760.000 placas.

9.  De quantas maneiras posso escolher uma sobremesa
entre duas tortas, quatro bolos e três sorvetes?
Problemas de Contagem

10.  De quantas maneiras posso escolher uma sobremesa
entre duas tortas, quatro bolos e três sorvetes?
↓ ↓ ↓
2 4 3
= 2+4+3 possibilidades
= 9 maneiras para escolha da sobremesa
Problemas de Contagem

11. FATORIAL
 O produto de dois inteiros positivos de 1 a n, inclusive, é
denotado por n! ( lê-se “n fatorial”):
n! = 1. 2 . 3. ...(n – 2).(n – 1).n
 Em outras palavras, n! é definido por:
1! = 1 e n! = n.( n – 1) !
 Também é conveniente definir 0! = 1 .
(LIPSCHUTZ E LIPSON, p. 135, 2004)

12.  Princípio da regra da soma
Para A e B conjuntos disjuntos, temos:
n ( A ∪ B) = n (A) + n (B)
 Princípio da regra do produto
Para A e B, temos o produto cartesiano de A e B:
n ( A x B) = n (A) x n (B)
Princípio Fundamental da Contagem

13.  Princípio da Multiplicação
Se existirem n1 resultados possíveis para um primeiro
evento e n2 para um segundo, então existem n1 . n2
resultados possíveis para a seqüência dos dois eventos.
Princípio Fundamental da Contagem
 Princípio da Adição
Se A e B são eventos disjuntos com n1 e n2 resultados
possíveis, respectivamente, então o número total de
possibilidades para o evento “A ou B” é n1 + n2.

14. Princípio Fundamental da Contagem
 Um aluno pode escolher uma entre duas camisetas da
UPF, uma vermelha e uma preta, e uma entre três pastas,
uma azul, uma amarela e uma verde. Quantos conjuntos
diferentes o aluno pode ter?

15. Princípio Fundamental da Contagem
 Um aluno pode escolher uma entre duas camisetas da
UPF, uma vermelha e uma preta, e uma entre três pastas,
uma azul, uma amarela e uma verde. Quantos conjuntos
diferentes o aluno pode ter?
= 2.3 possibilidades
= 6 conjuntos

16. Princípio Fundamental da Contagem:
Usando os dois princípios juntos
 Um aluno pode
escolher uma entre
duas camisetas da
UPF, uma vermelha e
uma preta, e uma
entre três pastas, uma
azul, uma amarela e
uma verde. Quantos
escolhas diferentes o
aluno pode fazer?

17. Princípio Fundamental da Contagem:
Usando os dois princípios juntos
 Um aluno pode
escolher uma entre
duas camisetas da
UPF, uma vermelha e
uma preta, e uma
entre três pastas, uma
azul, uma amarela e
uma verde. Quantos
escolhas diferentes o
aluno pode fazer?
= 2.3 possibilidades escolhendo primeiro a camiseta
= 3.2 possibilidades escolhendo primeiro a pasta
= 6 + 6 escolhas

18. Princípio Fundamental da Contagem:
Usando os dois princípios juntos
 Quantos inteiros de três dígitos(100 a 999) são pares?

19. Princípio Fundamental da Contagem:
Usando os dois princípios juntos
 Quantos inteiros de três dígitos(100 a 999) são pares?
= 9.10.1 = 90 números pares que terminam em 0
Considerando, analogamente, os que terminam em 2,4,6,e 8,
temos:
90 + 90 + 90 + 90 + 90 = 450 números pares

20. Problema 1: De quantas formas posso colocar em fila os alunos
do nível VI da Matemática(5 alunos)? E do nível
II(20 alunos)?
Problemas de Análise Combinatória
Problema 2: Em cada turma do ICEG será formada uma
comissão composta por um coordenador, um
secretário e um relator. Quantas comissões
diferentes poderão ser formadas na turma do nível
VI da Matemática(5 alunos)? E do nível II(20
alunos)?

21. Problema 4: Para cada turma do ICEG a UPF sorteou três
camisetas. Quantas são as possibilidades de
sorteio na turma do nível VI da Matemática(5
alunos)? E do nível II(20 alunos)?
Problemas de Análise Combinatória
Problema 3: Para cada turma do ICEG a UPF sorteou três
brindes: uma bolsa de estudos, uma camiseta e
uma caneca. Quantas são as possibilidades de
premiação para a turma do nível VI da
Matemática(5 alunos)? E do nível II(20 alunos)?

22. Problema 1: De quantas formas posso colocar em fila os alunos
do nível VI da Matemática(5 alunos)? E do nível II(20
alunos)?

23. Permutação: arranjo ordenado de objetos
A solução para o problema 1(que permutou
todos os n elementos do conjunto) é
 Nivel VI : P5 = 5!
 Nivel II : P20 = 20!
Genericamente, a permutação dos n
elementos de um conjunto é
Pn=n!

24. Problema 2: Em cada turma do
ICEG será formada
uma comissão
composta por um
coordenador, um
secretário e um
relator. Quantas
comissões diferentes
poderão ser formadas
na turma do nível VI da
Matemática(5 alunos)?
E do nível II(20
alunos)?
Cada uma dessas comissões
é uma permutação de 3
elementos distintos escolhidos
em um conjunto de 5 elementos.

25. Permutação: arranjo ordenado de objetos
A solução para o problema 2(que permutou r elementos
escolhidos entre os n objetos distintos do conjunto) é
Nível VI : P(5,3) = 5.4.3 =
Nível II : P(20,3) = 20.19.18 =
Genericamente, a permutação de r elementos de um conjunto
de n elementos(ou arranjo simples) é
P(n,r)=
60
!2
!2.3.4.5
)!35(
!5
==
−
6840
!17
!17.18.19.20
)!320(
!20
==
−
)!(
!
rn
n
−

26. ↓ ↓ ↓
5 4 3 possibilidades
= 5.4.3 possibilidades =
= 60 possibilidades no nível VI
Problema 3: Para cada turma do ICEG a
UPF sorteou três brindes:
uma bolsa de estudos, uma
camiseta e uma caneca.
Quantas são as
possibilidades de premiação
para a turma do nível VI da
Matemática(5 alunos)? E do
nível II(20 alunos)?
60
!2
!2.3.4.5
)!35(
!5
==
−

27. Problema 3: Para cada turma do ICEG a
UPF sorteou três brindes:
uma bolsa de estudos, uma
camiseta e uma caneca.
Quantas são as
possibilidades de premiação
para a turma do nível VI da
Matemática(5 alunos)? E do
nível II(20 alunos)?
↓ ↓ ↓
20 19 18 possibilidades
= 20.19.18 possibilidades =
= 6840 possibilidades no nível II
6840
!17
!17.18.19.20
)!320(
!20
==
−

28. Arranjo Simples (de n elementos tomados p a p,
p ≤ n, são os agrupamentos ordenados diferentes que se
podem formar com p dos n elementos dados)
Num conjunto de n elementos, ao agruparmos p a p:
 na primeira posição → n possibilidades
 na segunda posição → (n – 1) possibilidades
 na terceira posição → (n – 2) possibilidades
... ...
 na p-ésima posição → n – (p – 1) possibilidades

29. Arranjo Simples - An,p
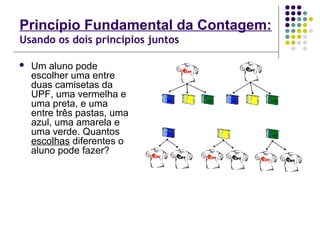
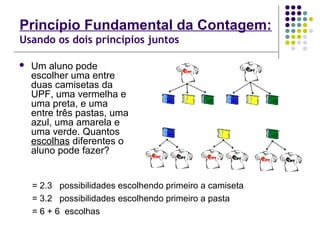
Aplicando o princípio fundamental da contagem, o número total
de possibilidades é dado por:
An,p = n(n – 1)(n – 2) ... [n – (p – 1)]
p fatores
ou An,p = n(n – 1)(n – 2) ... (n – p + 1)
( )
( )
( )
( )
( )!pn
n!
A
!pn
!pn1)p–(n...2)–1)(n–n(n
A
!pn
!pn
1).p–(n...2)–1)(n–n(nA
pn,
pn,
pn,
−
=
=
−
−+
=
=
−
−
+=

30. Problema 4: Para cada turma do
ICEG a UPF sorteou
três camisetas.
Quantas são as
possibilidades de
sorteio na turma do
nível VI da
Matemática(5 alunos)?
E do nível II(20
alunos)?
↓ ↓ ↓
Neste caso observe que os
dois agrupamentos de alunos
representados ao lado não
diferem um do outro, pois o
brinde é o mesmo. Então não
podem ser contados duas vezes.

31. Combinação Simples
Assim, precisamos
encontrar quantos subconjuntos
com 3 elementos podemos
formar com o grupo de 5
alunos.
Cada combinação dessas
dá origem a 6 arranjos. Isso
significa que o número de
arranjos de 5 elementos
tomados 3 a 3 é 6 vezes maior
que o número de combinaçoes
de 5 elementos tomados 3 a 3.

32. Combinação Simples
10
)!35(!3
!5
!3
)!35(
!5
6
.6
3
3,5
3,5
3,5
3,5
3,53,5
=
−
=
−
==
=
=
P
A
C
A
C
CA

33. Combinação Simples (de n elementos tomados
p a p, p ≤ n, são os subconjuntos com exatamente p
elementos que se podem formar com os n elementos dados)
)!(!
!
)!(!
!
!
)!(
!
!
,
,
,
pnp
n
C
pnp
n
n
pn
n
p
A
C
pn
pn
pn
−
=
−
=
−
==