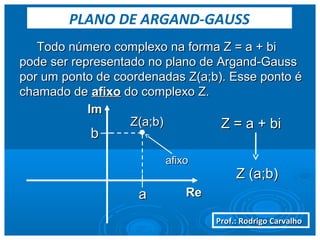
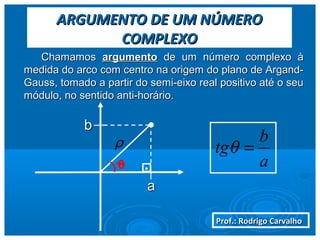
O documento apresenta os conceitos básicos de números complexos, incluindo: (1) sua forma algébrica como expressão Z = a + bi, onde a e b são números reais e i é a unidade imaginária; (2) definição de parte real e imaginária de um número complexo; (3) exemplos de números complexos; (4) operações entre números complexos como soma, subtração, multiplicação e divisão.

1. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
NÚMEROSNÚMEROS
COMPLEXOSCOMPLEXOS

2. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
A forma algébrica de um número complexo Z éA forma algébrica de um número complexo Z é
uma expressão da forma Z = a + bi, ondeuma expressão da forma Z = a + bi, onde aa ee bb sãosão
números reais enúmeros reais e ii é a unidade imaginária.é a unidade imaginária.
No número complexo Z = a + bi,No número complexo Z = a + bi, aa éé
chamada de parte real echamada de parte real e bb de parte imaginária.de parte imaginária.
aa Re(Z)Re(Z)
bb Im(Z)Im(Z)
DEFINIÇÃO
1i −=

3. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
ExemplosExemplos::
a) Z = - 3 + 5ia) Z = - 3 + 5i
Re(Z) = -3Re(Z) = -3
Im(Z) = 5Im(Z) = 5
b) Z = -i + 4b) Z = -i + 4
Re(Z) = 4Re(Z) = 4
Im(Z) = -1Im(Z) = -1
c) Z = 5c) Z = 5
Re(Z) = 5Re(Z) = 5
Im(Z) = 0Im(Z) = 0
d) Z = -6id) Z = -6i
Re(Z) = 0Re(Z) = 0
Im(Z) = -6Im(Z) = -6

4. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
OBSERVAÇÃOOBSERVAÇÃO::
1) Quando Im(Z) = 0, o número complexo será1) Quando Im(Z) = 0, o número complexo será
chamado dechamado de REALREAL..
2) Quando Re(Z) = 0 e Im(Z) = 0, o número2) Quando Re(Z) = 0 e Im(Z) = 0, o número
complexo será chamado decomplexo será chamado de IMAGINÁRIO PUROIMAGINÁRIO PURO..
Exemplo:Exemplo:
Determine as condições para que oDetermine as condições para que o
complexo Z = (2m + 1) + (-n + 3)i seja:complexo Z = (2m + 1) + (-n + 3)i seja:
a) Real;a) Real; b)Imaginário Puro.b)Imaginário Puro.
Ex: Z = 3Ex: Z = 3
Ex: Z = -7iEx: Z = -7i

5. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
Dizemos que os complexos Z = a + bi e W = c + diDizemos que os complexos Z = a + bi e W = c + di
são iguais se, e somente se, a = c e b = d, ou seja:são iguais se, e somente se, a = c e b = d, ou seja:
Re(Z) =Re(W)Re(Z) =Re(W)
Im(Z) = Im(W)Im(Z) = Im(W)
Z = WZ = W
**OBS.OBS.: Não podemos dizer que um número: Não podemos dizer que um número
complexo é maior ou menor que outro númerocomplexo é maior ou menor que outro número
complexo, ou seja, no conjunto C não existecomplexo, ou seja, no conjunto C não existe
relação de ordem.relação de ordem.
IGUALDADE ENTRE COMPLEXOS

6. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
1. SOMA E SUBTRAÇÃO1. SOMA E SUBTRAÇÃO
OPERAÇÕES ENTRE COMPLEXOS
Para somar ou subtrair dois complexos,Para somar ou subtrair dois complexos,
efetuaremos as partes reais entre si e as partesefetuaremos as partes reais entre si e as partes
imaginárias entre si.imaginárias entre si.
Exemplo:Exemplo: Sendo Z = 5 + 3i e W = 4 - i, temos:Sendo Z = 5 + 3i e W = 4 - i, temos:
Z+WZ+W = 5 + 3i + 4 - i5 + 3i + 4 - i = 9 + 2i9 + 2i
Z-WZ-W = 5 + 3i - (4 - i)5 + 3i - (4 - i) = 5 + 3i - 4 + i5 + 3i - 4 + i 1 + 4i1 + 4i=

7. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
2. MULTIPLICAÇÃO2. MULTIPLICAÇÃO
O produto entre dois complexos é obtidoO produto entre dois complexos é obtido
aplicando-se a distributiva entre seus termos.aplicando-se a distributiva entre seus termos.
**LEMBRE-SELEMBRE-SE:: ii22
== -1-1
Exemplo:Exemplo: Sendo Z = 3 + 2i e W = 1 + 4i, temos:Sendo Z = 3 + 2i e W = 1 + 4i, temos:
Z .WZ .W == (3 + 2i).(1 + 4i)(3 + 2i).(1 + 4i) == ==3 + 12i + 2i + 83 + 12i + 2i + 8ii22
== 3 + 12i + 2i + 8(-1)3 + 12i + 2i + 8(-1) = -5 + 14i-5 + 14i

8. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
Dado Z = a + bi, sendo i a unidade imaginária.Dado Z = a + bi, sendo i a unidade imaginária.
Chamamos o conjugado de Z, denotado por Z,Chamamos o conjugado de Z, denotado por Z,
ao complexo obtido pela troca de sinal da parteao complexo obtido pela troca de sinal da parte
imaginária de Z.imaginária de Z.
Z = a - biZ = a - bi
Exemplos:Exemplos:
a) Z = 3 + 2ia) Z = 3 + 2i ZZ = 3 – 2i3 – 2i
b) W = -5ib) W = -5i WW = 5i5i
c) K = 2c) K = 2 KK = 22
CONJUGADO DE UM COMPLEXO
**OBS.OBS.: Z = Z: Z = Z

9. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
3. DIVISÃO3. DIVISÃO
Para efetuarmos a divisão entre dois complexosPara efetuarmos a divisão entre dois complexos
Z e W, procederemos da seguinte maneira:Z e W, procederemos da seguinte maneira:
Z Z . WZ Z . W
W W WW W W
ConclusãoConclusão: Devemos multiplicar numerador e: Devemos multiplicar numerador e
denominador pelo conjugado do denominador.denominador pelo conjugado do denominador.

10. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
Exemplo:Exemplo: Dividir Z = 5 + 3i por W = 4 – 2i.Dividir Z = 5 + 3i por W = 4 – 2i.
ZZ
WW
5 + 3i5 + 3i
4 – 2i4 – 2i
. 4 + 2i4 + 2i
4 + 2i4 + 2i
20 + 10i + 12i + 6i20 + 10i + 12i + 6i22
4422
– (2i)– (2i)22
14 + 22i14 + 22i
16 - 4i16 - 4i22
14 + 22i14 + 22i
16 + 416 + 4
14 + 22i14 + 22i
20 2020 20
7 + 11i7 + 11i
10 1010 10
**OBSOBS.: Sempre que houver a unidade imaginária.: Sempre que houver a unidade imaginária
no denominador, realizaremos o processono denominador, realizaremos o processo
acima.acima.

11. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
ii00
=1=1
ii11
= i= i
ii22
= -1= -1
ii33
= i= i22
.i = (-1).i = -i.i = (-1).i = -i
ii44
= i= i22
.i.i22
= (-1).(-1) = 1= (-1).(-1) = 1
ii55
= i= i44
.i = 1.i = i.i = 1.i = i
ii66
= i= i44
.i.i22
= 1.(-1) = -1= 1.(-1) = -1
ii77
= i= i44
.i.i33
= 1.(-i) = -i= 1.(-i) = -i
……………………………….
ii1818
= i= i44
.. ii44
.. ii44
.. ii44
.. ii22
= -1= -1
POTÊNCIAS DO i

12. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
PROPRIEDADEPROPRIEDADE
Quando o expoente de i for maior do que 3,Quando o expoente de i for maior do que 3,
iremos dividí-lo por 4, sendo o resto destairemos dividí-lo por 4, sendo o resto desta
divisão o novo expoente de i.divisão o novo expoente de i.
663838 99
22
restoresto
Logo, iLogo, i278278
= i= i22
= -1.= -1.
Ex: iEx: i278278
= ?= ?
278 4278 4

13. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
**OBSOBS.: A soma de quaisquer 4 potências.: A soma de quaisquer 4 potências
consecutivas de i é sempre igual a zero.consecutivas de i é sempre igual a zero.
Ex: iEx: i55
++ii66
++ii77
++ii88
==00
ii3535
++ii3636
++ii3737
++ii3838
==00
GeneralizandoGeneralizando: i: inn
++iin+1n+1
++iin+2n+2
++iin+3n+3
= 0= 0

14. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
(1+ i)(1+ i)22
== 1 + 2i + i1 + 2i + i22
== 1 + 2i + (-1)1 + 2i + (-1) == 2i2i
== 1 - 2i + i1 - 2i + i22
== 1 - 2i + (-1)1 - 2i + (-1) == -2i-2i(1– i)(1– i)22
(1+ i)(1+ i)1010
== [[(1+ i)(1+ i)22
]]55
== (2i)(2i)55
== 32i32i55
== 32i32i11
== 32i32i
(1- i)(1- i)77
== [[(1- i)(1- i)22
]]33
..(1- i)(1- i) == ((-2i)-2i)33
.(1- i).(1- i) ==-8i-8i33
.(1- i).(1- i) ==
== -8.(-i).(1- i)-8.(-i).(1- i)== ==8i - 8i8i - 8i22 8i + 88i + 8
ALGUMAS POTÊNCIAS DE COMPLEXOS
Como o resultado é imaginário puro, podemosComo o resultado é imaginário puro, podemos
calcular outras potências:calcular outras potências:

15. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
Todo número complexo na forma Z = a + biTodo número complexo na forma Z = a + bi
pode ser representado no plano de Argand-Gausspode ser representado no plano de Argand-Gauss
por um ponto de coordenadas Z(a;b). Esse ponto épor um ponto de coordenadas Z(a;b). Esse ponto é
chamado dechamado de afixoafixo do complexo Z.do complexo Z.
ReRe
ImIm
Z = a + biZ = a + bi
Z (a;b)Z (a;b)
aa
bb
Z(a;b)Z(a;b)
afixoafixo
PLANO DE ARGAND-GAUSS

16. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
MÓDULO DE UM NÚMERO COMPLEXOMÓDULO DE UM NÚMERO COMPLEXO
Chamamos deChamamos de módulomódulo de um númerode um número
complexo a distância do afixocomplexo a distância do afixo do complexo àdo complexo à
origem do plano de Argand-Gauss.origem do plano de Argand-Gauss.
aa
bb
|z|
.
222
|| baz +=
(rô)ρouz

17. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
ARGUMENTO DE UM NÚMEROARGUMENTO DE UM NÚMERO
COMPLEXOCOMPLEXO
ChamamosChamamos argumentoargumento de um número complexo àde um número complexo à
medida do arco com centro na origem do plano de Argand-medida do arco com centro na origem do plano de Argand-
Gauss, tomado a partir do semi-eixo real positivo até o seuGauss, tomado a partir do semi-eixo real positivo até o seu
módulo, no sentido anti-horário.módulo, no sentido anti-horário.
aa
bb
ρ
0 . a
b
tg =θ

18. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
FORMA TRIGONOMÉTRICA DE UMFORMA TRIGONOMÉTRICA DE UM
NÚMERO COMPLEXONÚMERO COMPLEXO
Podemos representar um complexo em função do seuPodemos representar um complexo em função do seu
módulo e do seu argumento, chamada demódulo e do seu argumento, chamada de formaforma
trigonométricatrigonométrica de um número complexo.de um número complexo.
).(cos θθρ seniZ +=
Ex: Sendo o complexo Z = 2 – 2i, determine aEx: Sendo o complexo Z = 2 – 2i, determine a
sua forma trigonométrica .sua forma trigonométrica .

19. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
Na figura, estão representados, no plano complexo, os
pontos M, N e P, afixos dos números complexos m, n e p.
Sabendo-se que |m| = |n| = |p| = 1 e que θ = 45o
, pode-se
afirmar que
m – n + 2p é igual a:
θ θ
2i205)
i204)
i2103)
i202)
201)
−
−
−
−
−

20. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
OPERAÇÕES NA FORMAOPERAÇÕES NA FORMA
TRIGONOMÉTRICATRIGONOMÉTRICA
1. MULTIPLICAÇÃO1. MULTIPLICAÇÃO
).i.senθ(cosθρZe)i.senθ(cosθρZSejam 22221111 +=+=
)](.)[cos(.. 21212121 θθθθρρ +++= seniZZ
2. DIVISÃO2. DIVISÃO
)](.)[cos( 2121
2
1
2
1
θθθθ
ρ
ρ
−+−= seni
Z
Z

21. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
3. POTENCIAÇÃO (1ª fórmula de Moivre)3. POTENCIAÇÃO (1ª fórmula de Moivre)
:temosnulo,não
naturalnúmeroumne)i.senρ(cosθZSendo θ+=
)].(.).[cos( θθρ nseninZ nn
+=
.calcular Zi,
2
3
2
1
ZcomplexooSendo:Ex 6
+=

22. Prof.: Rodrigo CarvalhoProf.: Rodrigo Carvalho
4. RADICIAÇÃO (2ª fórmula de Moivre)4. RADICIAÇÃO (2ª fórmula de Moivre)
:temosnulo,não
naturalnúmeroumne)i.senρ(cosθZSendo θ+=
Z)k(
2
.
2
cos
∈











 +
+




 +
=
n
k
seni
n
k
Z nn πθπθ
ρ
Ex: Calcular as raízes cúbicas de 8 .Ex: Calcular as raízes cúbicas de 8 .