O documento apresenta conceitos fundamentais sobre funções afins e lineares, incluindo:
1) A história do termo "função" e sua criação por Gottfried Leibniz;
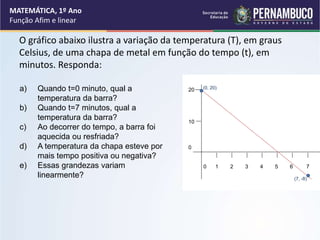
2) Exemplos de situações do dia-a-dia que podem ser representadas por funções;
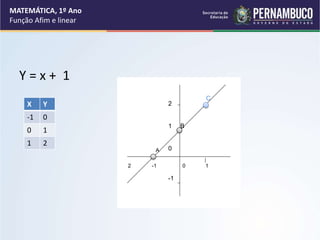
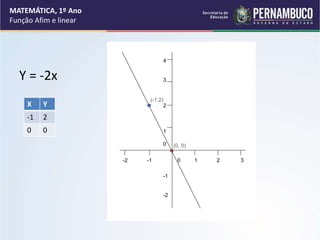
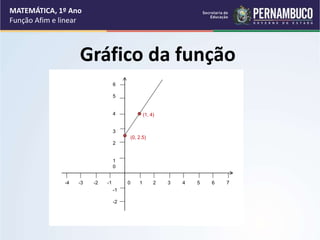
3) Definição formal de função afim e suas características principais como conjunto domínio, conjunto imagem, coeficientes angular e linear.