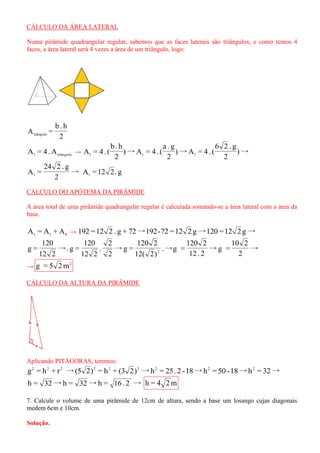
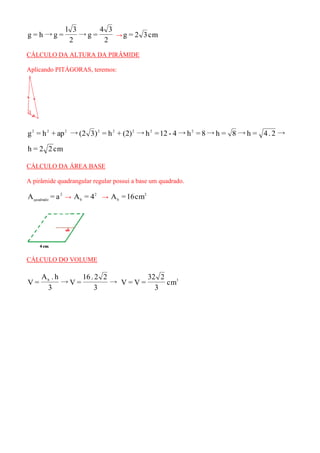
O documento discute o cálculo de medidas geométricas de pirâmides regulares, como altura, área lateral e total. Inclui exemplos de como calcular essas medidas para pirâmides triangulares, quadrangulares e de outros formatos, usando fórmulas como a de Pitágoras.

1. LISTA 1 - PIRÂMIDES – GABARITO
1. Calcular a medida da altura de um tetraedro regular sabendo que o perímetro da base mede 9cm.
SOLUÇÃO.
O tetraedro regular é a pirâmide triangular regular com todas as faces sendo triângulos equiláteros.
CÁLCULO DO APÓTEMA DA PIRÂMIDE
O apótema, g, da pirâmide é a altura do triângulo equilátero.
2
3 3
=
2
l 3
g = → cm
2
3 3
g =
CÁLCULO DO APÓTEMA DA PIRÂMIDE
O apótema da base, ab, é a terça parte da altura da base (também mediana).
2
3
=
6
3 3
) =
2
3 3
.(
3
1
) =
2
l 3
.(
3
1
ap = → cm
2
3
ap =
CÁLCULO DA ALTURA DA PIRÂMIDE
Aplicando PITÁGORAS, teremos:
4
3
-
4
9.3
) →h =
2
3
) = h + (
2
3 3
g = h + ap → ( 2 2 2 2 2 2 2
→
4
24
→h =
4
24
→h =
4
3
-
4
27
h = 2 2 h = 6 cm

2. 2. Determinar a área lateral e total de uma pirâmide triangular regular de 7cm de apótema, sendo 2cm o
raio do círculo circunscrito à base.
Solução.
CÁLCULO DA ARESTA DA BASE
O apótema da pirâmide é a altura da face. A aresta da base pode ser calculada em função do raio.
Utilizando essas informações, temos:
a = r 3→a = 2 3cm
CÁLCULO DA ÁREA BASE
A pirâmide triangular regular possui a base como um triângulo equilátero.
4
a 3
A =
2
triânguloequilátero
4
a 3
A =
2
b →
( )
4
2 3 3
A =
2
b →
4
4 .3 3
A = b →
4
12 3
A = b →
2
b A = 3 3cm
CÁLCULO DA ÁREA LATERAL
Num pirâmide triangular regular, sabemos que as faces laterais são triângulos, e como temos 3 faces no
tetraedro regular, a área lateral será 6 vezes a área de um triângulo, logo:

3. 2
b . h
A = tiângulo
l retângulo A = 3.A → )→
2
2 3 . 7
)→A = 3. (
2
a . g
)→A = 3. (
2
b . h
A = 3. ( l l l A = 21 3cm l
CÁLCULO DA ÁREA TOTAL
A área total de uma pirâmide triangular regular é calculada somando-se a área lateral com a área da
base.
t l b A = A + A → A = 21 3 + 3 3 t →
2
t A = 24 3cm
3. O volume de uma pirâmide quadrangular regular é 144m³ e a altura é o dobro da aresta da base.
Calcule a altura dessa pirâmide.
Solução.
A base da pirâmide quadrangular regular é um quadrado.
2
quadrado A = a → 2
b A = a
3
A . h
V = b
→ →144 .3 = 2a →2a = 432
3
a . 2a
144 = 3 3
2
→a = 216→a = 216→
2
432
a = 3 3 3 a = 6cm
h = 2a→h = 2. 6→ h =12cm
5. Uma pirâmide regular de base quadrada tem lado da base medindo 8 cm e área lateral igual a
5
3 da
área total. Calcular a altura e a área lateral desta pirâmide.
Solução.
A área total é a soma da área lateral com a área da base.

4. CÁLCULO DA ÁREA BASE
A pirâmide quadrangular regular possui a base um quadrado.
2
quadrado A = a → 2
b A = a → 2
b A = 8 → 2
b A = 64cm
CÁLCULO DA ÁREA LATERAL
Numa pirâmide quadrangular regular, sabemos que as faces laterais são triângulos, e como temos 4
faces, a área lateral será 4 vezes a área de um triângulo, logo:
2
b . h
A = tiângulo
l triângulo A = 4.A → →
2
32 . g
)→A =
2
8. g
)→A = 4 . (
2
a . g
)→A = 4 . (
2
b . h
A = 4 . ( l l l l
A =16g l
CÁLCULO DA ÁREA TOTAL
A área total é calculada efetuando-se a soma da área lateral com a área da base.
A = A + A →A = 64 +16g t l b t
CÁLCULO DO APÓTEMA DA PIRÂMIDE
Do enunciado tiramos que a área lateral é
5
3 da área total, logo:
→16g .5 = 3. (64 +16g)→80g =192 + 48g→
5
3
→16g = (64 +16g) .
5
3
A = A . l t
→
32
192
80g =192 + 48g→80g 48g =192→32g =192→g = g = 6 cm
CÁLCULO DO APÓTEMA DA BASE
O apótema da base é igual à metade do lado do quadrado.
→
2
8
→a =
2
l
a = b b a = 4 cm b
CÁLCULO DA ALTURA DA PIRÂMIDE
Aplicando PITÁGORAS, teremos:

5. g = h + ap →(6) = h + (4) →h = 36 -16→h = 20→h = 20→h = 4.5→ 2 2 2 2 2 2 2 2
h = 2 5cm
6. Sendo 192m² a área total de uma pirâmide quadrangular regular e 3 2 m o raio do círculo inscrito na base,
calcule a altura da pirâmide.
Solução.
A aresta da base quadrada pode ser calculada em função do raio.
CÁLCULO DA ARESTA DA BASE
A aresta da base é igual ao diâmetro da circunferência, logo:
a = d = 2r→a = 2. (3 2 )→a = 6 2 m
CÁLCULO DA ÁREA BASE
A pirâmide quadrangular regular possui a base um quadrado.
2
quadrado A = a → 2
b A = a → 2
b A = (6 2) → A = 36. 2 b → 2
b A = 72m

6. CÁLCULO DA ÁREA LATERAL
Numa pirâmide quadrangular regular, sabemos que as faces laterais são triângulos, e como temos 4
faces, a área lateral será 4 vezes a área de um triângulo, logo:
2
b . h
A = tiângulo
l triângulo A = 4.A → )→
2
6 2 . g
)→A = 4 . (
2
a . g
)→A = 4 . (
2
b . h
A = 4 . ( l l l
→
2
24 2 . g
A = l A =12 2. g l
CÁLCULO DO APÓTEMA DA PIRÂMIDE
A área total de uma pirâmide quadrangular regular é calculada somando-se a área lateral com a área da
base.
t l b A = A + A → 192 =12 2 . g + 72→192-72 =12 2 g→120 =12 2 g→
→
2
10 2
→g =
12 . 2
120 2
.→g =
12( 2)
120 2
→g =
2
2
.
12 2
120
→. g =
12 2
120
g = 2
→
2 g = 5 2m
CÁLCULO DA ALTURA DA PIRÂMIDE
Aplicando PITÁGORAS, teremos:
g = h + r →(5 2) = h + (3 2) →h = 25. 2 -18→h = 50 -18→h = 32→ 2 2 2 2 2 2 2 2 2
h = 32→h = 32→h = 16. 2 → h = 4 2m
7. Calcule o volume de uma pirâmide de 12cm de altura, sendo a base um losango cujas diagonais
medem 6cm e 10cm.
Solução.

7. CÁLCULO DA ÁREA BASE
A pirâmide possui a base um losango, logo: a área do losango é calculada como a metade do produto de
suas diagonais.
2
D. d
A = losango → b losango A = A →
2
D. d
A = b →
2
60
→A =
2
10 . 6
A = b b → 2
b A = 30cm
CÁLCULO DO VOLUME
→V = 30 . 4
3
30 .12
→V =
3
A . h
V = b
→ 3 V =120cm
8. Calcule o volume de uma pirâmide quadrangular regular cujas faces laterais são triângulos equiláteros
de lado 4, em centímetros quadrados.
Solução.
CÁLCULO DO APÓTEMA DA BASE
O apótema da base é igual à metade do lado do quadrado.
→
2
4
→a =
2
l
a = b b a = 2 cm b
CÁLCULO DO APÓTEMA DA PIRÂMIDE
Se as faces laterais da pirâmide são triângulos equiláteros, então o apótema da pirâmide, g, será a altura
desse triângulo. As arestas da base possuem a mesma medida do lado do triângulo. Temos:

8. 2
4 3
→g =
2
l 3
g = h→g = →g = 2 3cm
CÁLCULO DA ALTURA DA PIRÂMIDE
Aplicando PITÁGORAS, teremos:
g = h + ap →(2 3) = h + (2) →h =12 - 4→h = 8→h = 8→h = 4. 2→ 2 2 2 2 2 2 2 2
h = 2 2 cm
CÁLCULO DA ÁREA BASE
A pirâmide quadrangular regular possui a base um quadrado.
2
quadrado A = a → 2
b A = 4 → 2
b A =16cm
CÁLCULO DO VOLUME
→
3
16 . 2 2
→V =
3
A . h
V = b 3 cm
3
32 2
V = V =