1) O documento apresenta os principais conceitos de cálculo 1, incluindo conjuntos numéricos, funções, pares ordenados e sistema cartesiano. 2) São definidos os conjuntos dos números naturais, inteiros, racionais, irracionais e reais. 3) São explicados os conceitos de par ordenado, sistema cartesiano e tipos de funções como polinomiais, racionais, exponenciais e logarítmicas.

1. UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
Campus Toledo
Disciplina: Cálculo 1 Turma: P13
Professora Aracéli Ciotti de Marins
CÁLCULO 1
Toledo, 1/2010

2. Capítulo 1 – Conjuntos Numéricos e Funções
1. Sistematização dos Conjuntos Numéricos
1.1. Números Naturais ()
Este conjunto é de grande importância pelo seu uso na contagem. Sua notação é: N = 0, 1,
2, 3, ....
Quando não se utiliza o número 0 (zero), a notação utilizada é:
N* = N – 0 = 1, 2, ....
1.2. Números Inteiros ()
O conjunto dos números inteiros é formado pelos elementos do conjunto dos naturais
acrescidos de seus simétricos.
Notação: Z = ..., -2, -1, 0, 1, 2, ....
Quando o elemento zero não pertence ao conjunto, a notação se torna: Z* = Z – 0.
1.3. Números Inteiros ()
Quando se considera o conjunto dos números positivos, acrescidos do zero, a notação é:
Z+ = N.
Quando o elemento zero não pertence ao conjunto, a notação torna-se: (inteiros
positivos).
Analogamente, o conjunto dos inteiros não-positivos é: Z - = ..., -2, -1, 0 e este conjunto
sem o zero é o conjunto dos negativos:
1.4. Números Racionais ou Fracionários (Q)
São todos os números que podem ser escritos sob a forma de fração entre dois números
inteiros. Tem representação decimal finita ou dízima periódica.
A notação deste conjunto é:
p 
Q   / p Z  q Z*
q 
Exemplos: 2; -4; 0,5; 1,37; 1,5999...; 0,212121..., etc.
1.5. Números Irracionais
São os números cuja representação decimal não é exata nem periódica, conseqüentemente
não podem ser escritos como uma fração entre dois inteiros.
Exemplos:  = 3,14159265..., e = 2,718281828..., 2  1,4142135624... , etc.
1.6. Números Reais (R)
Representam a união entre os números Racionais e Irracionais: R = Q  I.
2

3. Exercícios
1. Determine se é verdadeira (V) ou falsa (F) cada uma das afirmações, justificando sua
resposta:
( )–7N
( ) 2 Q
( )5Z
( ) -8  Q
( ) 3  R
( )-I
( )–7Z
( ) 3  Q
2. Faça um esquema que represente a sistematização do conjunto dos números Reais,
decompostos em outros conjuntos.
3

4. 2. Par Ordenado e Sistema Cartesiano
Par Ordenado
Par é todo conjunto formado por dois elementos {a, b}, não importando a ordem que a e b
aparecem no conjunto, assim, são iguais os conjuntos: {a, b} = {b, a}. Porém, quando a
ordem dos elementos importa, o par passa a ser chamado de par ordenado.
Exemplo: Seja o par {x, y} a solução do sistema:
2 x  3 y  4

 x  3 y  7
Verifica-se que x = -1 e y = 2 é solução, ao passo que x = 2 e y = -1 não é. Assim, com
notação de conjuntos, temos que:
{-1, 2} = {2, -1}, o que não deve ocorre neste casso, então, utilizamos a notação
(-1, 2) para representar o par ordenado (x,y). Logo (-1,2)(2,-1).
Propriedade: Se (a, b) = (c, d) então a = c e b = d.
Exemplo: Determine a e b se: (a + 2, 18) = (0, 3b).
Sistema Cartesiano Ortogonal: É um sistema formado por dois eixos, x e y, perpendiculares
entre si:
O eixo x é denominado eixo das abscissas e o eixo y é denominado eixo das ordenadas.
Estes eixos dividem o plano em quatro regiões, chamadas quadrantes. Este sistema é
utilizado para localizar pontos, com abscissas e ordenadas conhecidas.
Exemplo: Faça um sistema cartesiano ortogonal, e nele localize os pontos: A(3,0), B(0,-2),
C(2,2), D(-2,-3), E(1,-4), F(-3,4).
Exercícios
1. Determine a e b:
a) (a, b) = (1, 3)
b) (2a – 2, b + 3) = (3a + 5, 2b – 7)
c) (2a, a – 8) = (1 – 3b, b)
2. Determine se as sentenças são verdadeiras (V) ou falsas (F):
a) ( ) (-5, 4)  3 quadrante;
b) ( ) os pontos de abscissas negativas e ordenadas positivas pertencem ao 1º
quadrante;
c) ( ) um ponto no 4º quadrante tem abscissa positiva e ordenada negativa.
4

5. 3. Funções
Uma função pode ser definida como uma correspondência de um conjunto A de
números Reais x a um conjunto B de números Reais y, em que o número y é único para um
valor específico x. Formalmente, defini-se uma função como um conjunto de pares
ordenados de números (x, y), sendo que dados dois pares ordenados distintos, nenhum deles
terá o mesmo primeiro número.
Definição: Uma função f é uma lei a qual para cada elemento x de um conjunto
A faz corresponder exatamente um elemento chamado f(x), em um conjunto B.
O conjunto de todos os valores admissíveis de x será chamado de domínio da
função e o conjunto de todos os valores resultantes de y é chamado a imagem da função.
O símbolo que representa um número arbitrário no domínio de f é chamado variável
independente, e o que representa um número qualquer na imagem de f é chamado variável
dependente.
Existem quatro maneiras de representar uma função:
a) verbalmente: descrevendo-a por palavras;
b) numericamente: por meio de tabelas de valores;
c) visualmente: através de gráficos;
d) algebricamente: utilizando-se uma forma escrita.
x2
Exemplo: Seja a função f definida pela regra: f  x   . Observa-se que os
x
 8
pares ordenados (1, 3), (-1, -1), (2, 2),  6,  pertencem à função f, já os pares ordenados
 6
(1, 2), (5, 3), (5, 9), dentre outros, não pertencem à f. O domínio da função f é composta por
todos os valores possíveis de serem substituídos no lugar de x, e verificamos que isto é
possível para todos os números reais, exceto para o número zero, que quando substituído
em x, na função, resultaria em 2 dividido por zero, o que sabemos ser uma divisão
impossível de ser resolvida. Então, formalmente, o domínio de f, denotado por Dom[f] é
igual a x   / x  0 que lê-se x pertencente aos Reais, tal que x é diferente de zero.
Observa-se também que, todos os reais fazem parte da imagem de f, pois seja qual for o
valor de y escolhido, há um valor de x correspondente. Então a imagem de f, denotada por
Im[f] é igual ao conjunto de todos os reais.
5

6. O gráfico de uma função f é o conjunto de todos os pontos (x, y) em R2 para os
quais (x, y) é um par ordenado de f.
A raiz de uma função f é o número x para o qual f(x) = 0. Graficamente, a raiz é
o local em que o gráfico intercepta o eixo x.
O intercepto y de uma função f é o valor em que o gráfico “corta” o eixo y e
corresponde ao valor de f(0).
a. Tipos de Funções
a) Funções Polinomiais: São funções em que a regra é descrita por um polinômio.
Exemplos: f  x   x 5  6 x 4  3 x 2  x  4 , g  x   x  4 , h x   6  x  2 x 2  x 10 .
As funções polinomiais subdividem-se em:
a. Função Constante: É toda função em que y não sofre variação quando x
varia, ou seja, o valor de y continua constante para todos os valores de x. É
escrita como f(x) = c. Seu gráfico é uma reta paralela ao eixo x, que
intercepta o eixo y em c.
b. Função Afim: É também conhecida como função do 1º grau. É toda função
do tipo: f(x) = ax + b, com a  0. O gráfico de uma função afim é sempre
uma reta, em que a é chamado coeficiente angular ou inclinação da reta e é o
valor que representa a taxa de variação de y com respeito a x. b é conhecido
como coeficiente linear da reta e o número no qual a reta intercepta o eixo y.
b
A raiz da função afim é: x  .
a
c. Função Linear: São funções afim com b = 0, ou seja: f(x) = ax. Seu gráfico
sempre passa pela origem.
d. Função Quadrática: É uma função polinomial de grau 2; É escrita como
f x   ax 2  bx  c , com a  0. O gráfico de uma função do 2º grau é uma
parábola. O intercepto y é o valor de c. As raízes são obtidas pela fórmula:
6

7. b    b  b 2  4ac
x1, 2  , sendo   b 2  4ac , assim: x1, 2  . Há três
2a 2a
possibilidades para :
i.  = 0 e a função terá duas raízes reais e iguais.
ii.  > 0 e a função terá duas raízes reais e distintas.
iii.  < 0 e a função não terá raízes. O gráfico ficará todo acima ou todo
abaixo do eixo x, conforme valor de a.
A concavidade da parábola é verificada da seguinte forma:
i. Se a > 0, a parábola tem concavidade voltada para cima e um ponto mínimo V;
ii. Se a < 0, a parábola tem concavidade voltada para baixo e um ponto máximo V.
b 
As coordenadas do vértice V da parábola são: xV  e yV 
2a 4a
Para construir a parábola seguem-se os passos:
iii. Verificar a concavidade utilizando a;
iv. Verificar o local em que a parábola intercepta o eixo x utilizando os zeros;
v. Calcular as coordenadas do vértice;
vi. Traçar a reta que passa por V e é paralela ao eixo y, que é o eixo de simetria da
parábola;
vii. c é o local em que a parábola intercepta o eixo y.
b) Funções Racionais: São funções que podem ser escritas como a divisão entre duas
x 2  3x  1 3x  4
funções polinomiais. Exemplos: f  x   , g x   .
x5 x 1
c) Funções Algébricas: São funções cujas regras envolvem somas, divisões,
3x  4
radiciações com funções racionais. Exemplos: f x   ,
5
1

g x   6 x  4 x 2 

2 .
7

8. d) Funções Transcendentes: São as funções logarítmicas, as exponenciais, as
trigonométricas, em geral, as que não são escritas pelo uso de polinômios.
a. Funções Exponenciais: Uma função é chamada de função exponencial, se
for definida por: f (x) = ax em que a é uma constante positiva diferente de 1.
a é chamada base do exponencial. Exemplos: f (x) = 2x; f (x) = (½) x. O
gráfico de uma função exponencial f(x) = ax é crescente, ou decrescente em
todo o domínio, conforme o caso:
i. Se a > 1, a função é crescente;
ii. Se 0 < a < 1, a função é decrescente.
Leis dos Expoentes: Se a e b forem números positivos e x e y números reais quaisquer,
então:
i. ax+y=axay;
ii. (ax)y=axy;
iii. (ab)x=axbx;
x
iv. a x  y  a
ay
Dentre todas as bases possíveis para a função exponencial, há uma mais utilizada no
cálculo, é a base e. Assim, com a base e: f(x) = ex e esta última função é chamada
exponencial natural.
Aplicações: A função exponencial ocorre freqüentemente em modelos matemáticos da
natureza e da sociedade, tais como crescimento populacional, decaimento radioativo, dentre
outras.
b. Função Logarítmica: é a função inversa da função exponencial. Definição:
Seja a  R, tal que a > 0 e a  1. Chamamos função logarítmica de base a
a função f, tal que para todo x  R: f  x   log a
x
Observações:
i. log a  y  a y  x ;
x
x
ii. log a  x ;
a
x
iii. a log a  x ;
iv. a raiz é sempre no número 1, pois f  x   log a  f 1  log 1  0
x
a
8

9. Leis dos Logaritmos: Se x e y forem números positivos, então:
xy x y
i. log a  log a  log a
x
y x y
ii. log  log a  log a
a
r
x x
iii. log a  r log a (em que r é um número real)
Logaritmos Naturais: Quando a base do logaritmo for o número natural e, o logaritmo é
x
chamado de logaritmo natural, e escrito como: log e  ln x
e) Funções Trigonométricas
A Função Seno é uma função tal que para todo x f  x   senx . No ciclo
trigonométrico, o valor de sen x representa a ordenada y, que varia entre -1 e 1:
Consideremos a função f(x)=sen x. O gráfico dessa função é o seguinte
O domínio da função seno é R e a imagem é o intervalo [-1,1]. Trata-se de uma função
limitada e periódica de período P=2π .
Para a função do tipo f(x) = sen (x + k), onde k é uma constante, existe uma translação
horizontal no gráfico da função f(x)= sen x, por exemplo:
9

10. Para a função do tipo f(x) = sen x + k, onde k é uma constante, existe uma translação
vertical no gráfico da função f(x)= sen x, por exemplo:
Para a função do tipo f(x) = k.sen x, onde k é uma constante, existe uma mudança de
inclinação no gráfico da função f(x)= sen x., Por exemplo:
A função Cosseno é uma função tal que para todo x f  x   cos x . No ciclo trigonométrico,
o valor de cos x representa a abscissa x, que varia entre -1 e 1:
O gráfico dessa função é o seguinte:
O domínio da função cosseno é R e a imagem é o intervalo [-1,1]. Trata-se de uma
função limitada e periódica de período P=2π . As translações e mudanças de inclinação
sofridas pelo gráfico da função cosseno, quando da existência de uma constante k, são
semelhantes às ocorridas com a função seno.
10

11. A função Tangente
senx
É uma função tal que para todo x f  x   tgx  . No ciclo trigonométrico tem-se:
cos x
O gráfico dessa função é o seguinte:
  
O domínio da função tangente é  x  R : x   k , k  Z  e a imagem é o conjunto R.
 2 
Trata-se de uma função periódica de período p = .
1 cos x
A função Cotangente é uma função tal que para todo x f  x   cot gx   . O ciclo
tgx senx
trigonométrico e o gráfico são dados a seguir:
1
A função Secante é uma função tal que para todo x f  x   sec x  . O ciclo
cos x
trigonométrico e o gráfico são dados a seguir:
11

12. 1
A função Cossecante é uma função tal que para todo x f  x   cos cx  . O ciclo
senx
trigonométrico e o gráfico são dados a seguir:
f) Funções definidas por partes
São funções que não são definidas por apenas uma sentença, assim, para encontrar o
valor da função em um determinado número, é necessário verificar à qual das sentenças ou
regras ele deve ser aplicado.
2 x, se x  2

Exemplo: f  x   5, se x  2
 x  4, se x  2

Um dos principais exemplos de funções definidas por partes são as funções
modulares, também conhecida como função valor absoluto, é dada por:
x se x  0
f x   x  
 x se x  0
b. Simetria de funções
a) Uma função é dita par quando f(-x) = f(x)
b) Uma função é dita ímpar quando f(-x) = - f(x)
Obs.: Quando uma função não é par nem ímpar é chamada assimétrica
c. Funções Crescentes e Decrescentes
a) Uma função f é chamada crescente em um intervalo I se:
f(x1) < f(x2) sempre que x1 < x2 em I
b) Uma função f é chamada decrescente em um intervalo I se:
f(x1) > f(x2) sempre que x1 < x2 em I
12

13. d. Composição de funções: Dadas duas funções f e g a função composta, denotada
por f o g, é definida por:
 fog x   f g x 
x 1
Exemplo: Dadas as funções f  x   x  3 e g  x   , temos que:
3
  fog x   f g x   g x   3   x  1  3  x  1 9  x  8 ;
 
 3  3 3
f x   1 x  3  1 x  2
 gof x   g  f x    
3 3 3
e. Inversão de funções: Dada uma função f a inversa de f é a função denotada por f -1
 
tal que f f 1  x   x .
Exemplo: Determine a inversa de f  x   2 x  3 .
Resolução:
 x   x
f f 1
2 f  x   3  x
1
2f 1
x   x  3
f 1
x   x  3
2
13

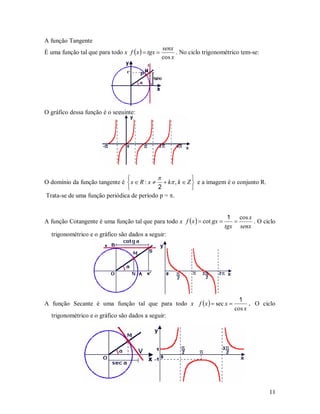
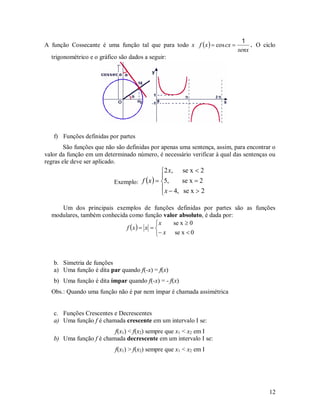
14. Exercícios
1. Os registros de temperatura T (em ºF) foram tomados de duas em duas horas
a partir da meia noite até as 14 horas, em Dallas, em 2 de junho de 2001. O
tempo foi medido em horas após a meia noite:
t 0 2 4 6 8 10 12 14
T 73 73 70 69 72 81 88 91
Use os registros para esboçar um gráfico de T como uma função de t, e use o gráfico
para estimar a temperatura as 11 horas da manhã.
2. Se f(x) = 3x3 – x + 2, encontre f(2), f(-2), f(a), f(-a), f(a + 1), 2f(a), f(2a),
f(a2), [f(a)]2 e f(a + h).
3. Encontre o domínio das funções:
a. f  x   x  3 ; 2
c. f x   .
b. f(t) = t2 – 6t x4
4. Uma caixa aberta em cima, tem um volume de 10 m3. O comprimento da
base é o dobro da largura. O material da base custa R$ 10,00 por metro
quadrado, ao passo que o material das laterais custa R$ 6,00 por metro
quadrado. Expresse o custo total do material em função da largura da base.
5. Faça o gráfico das funções abaixo:
a. f  x   x
b. f x   x  1 d. f x   x  1
c. f x   x  1 e. f x   x  1
2 x  1 se x  2 x  4 se x  6
 g. f x   
f. f  x   5 se x  2 5  x se x  6
x  2 se x  2

 x se x  -1 4  x se x  1
4 se x  -1  6 se x  1

 

h. g  x    x  1 se - 1  x  2 i. g x    x  1 se - 1  x  3
 2 se x  2 3 se x  2
 
3 x
 se x  2 x
 se x  2
14

15. f x    x 2  2 x  8
6. Faça o gráfico de cada uma das funções: f  x   x 2  6 x  9
f x   x 2  x  6
7. A parábola f(x) = x2 - 4x + 3 e a reta f(x) = ax + b cruzam os eixos
cartesianos nos mesmos pontos. Qual é a equação da reta?
8. Curva de aprendizagem é um conceito criado por psicólogos que
constataram a relação existente entre a eficiência de um indivíduo e a
quantidade de treinamento ou experiência possuída por este indivíduo. Um
exemplo de curva de aprendizagem é dado pela expressão:
Q x   700  400e 0 ,5 x . Nesta expressão, Q é quantidade de peças
produzidas por um funcionário, x é o tempo de experiência e e = 2,7183.
a. Quantas peças um funcionário com 2 meses de experiência deverá
produzir mensalmente?
b. E um funcionário sem experiência?
c. Compare os cálculos, e verifique se há coerência.
9. Encontre f + g, f – g, fg e f/g, e estabeleça os domínios:
a. f  x   x 3  2x 2 , g  x   3 x 2  1
b. f x   1 x , g x   1 x
10. Encontre as funções f o g, g o f, f o f, e g o g; e seus domínios:
a. f  x   2 x 2  x , g  x   3 x  2
1
b. f  x   1 x , g  x  
x
11. Faça um esboço do gráfico de f  x   cos x   2 e determine o domínio e a
imagem.
12. Determine a imagem e o domínio das funções:
a. f(x) = sec x
b. f(x) = tg x
c. f(x) = cotg x
d. f(x) = sec x
13. Classifique as informações como V (verdadeiras) ou F(falsas):
a. ( ) –1  D (sec x)
b. ( ) 3  Im (sec (x + 3))
c. ( ) –4  Im ((senx) + 3)
d. ( ) 90°  D(tg x)
15

16. 14. Quais os deslocamentos que ocorrem no gráfico de f(x) = cos x se:
a. f (x) = (cos x) + k
b. f (x) = cos (x + k)
c. f (x) = k cos x
15. Considere f  x   x 2  2 x  1 e g x   2 x  3 .
a. Determine g  x 
1
b. Determine gof
c. Classifique f quanto à simetria
d. f é crescente, decrescente ou assimétrica?
g
  x 
 
e. Determine  f 
f x  h   f x 
f. Calcule h
16. Dada a função g  x   5 x  6 , determine:
a. g 0
3
b. g  
 5 
c. g  x  7 
d. O ponto (x, 0)
e. O ponto (1,x)
17. Determine as raízes e os interceptos y, das funções abaixo, caso existam:
a. f  x   log 3
x
b. f x   x 2  2 x  3
18. O número y de alunos reprovados em CDI I está baseado na quantidade x de
pessoas que costumam conversar nas aulas, sendo que y será dado pela
função y = f(x):
1,4 x  5, se 0  x  10
f x   
47, se x  10
a. Faça um gráfico de reprovados versus o número de conversadores;
b. Estime a quantidade de reprovados, baseado no número de
conversadores.
16

17. 19. Sejam f  x   x 2  2 x  3 e g  x   x  8 . Determine:
a. Dom f 
b. fog ;
c. gof ;
1
d. g ;
e. diga se as funções encontradas nos itens (b) e (c) são pares, ímpares ou
assimétricas;
f. Esboce o gráfico de gog .
20. Determine a equação da reta abaixo:
21. Determine as raízes das funções abaixo, e onde o gráfico intercepta o eixo y:
a. f x   x 2  5x  6
a. f x  x 2  x  6
b. f(x) = 3x
c. f x   x 2  3x  2
d. f x  2 x  5
e. f(x) = 4
22. Suponha que você recebeu uma oferta para trabalhar por apenas um mês.
Qual das seguintes formas de pagamento você prefere?
I – Um milhão de dólares no fim do mês.
II – Um centavo de dólar no primeiro dia do mês, dois centavos no segundo dia,
quatro no terceiro dia e em geral, 2n – 1 centavos de dólar no n-ésimo dia.
23. Se a população de bactérias começa com 100 e dobra a cada três horas, então
t
o número de bactérias após t horas é n  f t   100  2 3, quando a população
atingirá 50000 bactérias?
17

18. 24. Qual a inversa de cada função dadas pelas regras abaixo?
a. f  x   2 x  3
x5
b. f x 
3
25. Calcule o valor da função f nos números indicados:
a. f x   6 x  3 no número -1
b. f  z   z 3  4 z 2  z  12 no número -2
w4
c. f w  no número -4
w 4
26. Classifique as funções abaixo quanto a simetria:
a. f  x   x
b. f x   3x  5
c. f x   x 3  2 x
27. Sabendo que f é uma função afim, que f 2   1 e f  1  3 , determine f.
28. Mostre se as funções dadas pelas regras abaixo são crescentes ou
decrescentes:
a) f  x   2 x  4
b) f  x    x  2