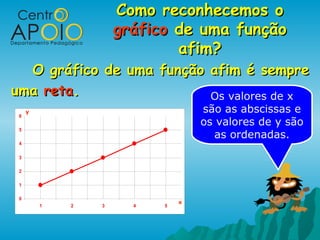
O documento aborda a função afim, explicando sua definição, representação e como construir gráficos. Ele também ensina a identificar coeficientes angular e linear, além de resolver sistemas e inequações do 1º grau. Exemplos práticos são fornecidos para ilustrar conceitos como a determinação de pontos e características das funções.

1. Função AfimFunção Afim

2. Ao final dessa aula vocêAo final dessa aula você
saberá:saberá:
 O que é uma função afim e todas as formasO que é uma função afim e todas as formas
de representá-la.de representá-la.
 Como identificar e construir gráficos daComo identificar e construir gráficos da
função afim.função afim.
 O que é coeficiente angular, coeficienteO que é coeficiente angular, coeficiente
linear e zero da funçãolinear e zero da função
 Identificar se uma função é crescente ouIdentificar se uma função é crescente ou
decrescente.decrescente.
 Resolver sistemas através deResolver sistemas através de
gráficosgráficos
 Resolver inequações do 1º grau.Resolver inequações do 1º grau.

3. O que éO que é função afimfunção afim??
É a função definida por uma expresão doÉ a função definida por uma expresão do
1º grau1º grau..
Exemplos:Exemplos:
 f(x) = x +1f(x) = x +1
 y=y=
5+m
m
É apresentada na
forma:
f(x) = ax + b

4. Como reconhecemos oComo reconhecemos o
gráficográfico de uma funçãode uma função
afim?afim?
O gráfico de uma função afim é sempreO gráfico de uma função afim é sempre
umauma retareta..
0
1
2
3
4
5
6
1 2 3 4 5
x
y
Os valores de x
são as abscissas e
os valores de y são
as ordenadas.

5. ComoComo construímosconstruímos oo
gráficográfico de uma funçãode uma função
afim?afim?
Basta acharBasta achar dois pontosdois pontos queque pertençam àpertençam à
retareta da função dada.da função dada.
Exemplo: Sendo a função f(x) = 2x + 1.Exemplo: Sendo a função f(x) = 2x + 1.
1º passo:1º passo: escolherescolher doisdois valoresvalores parapara xx..
x = 0 e x = 1x = 0 e x = 1

6. f(0) = 2.0 + 1 = 1f(0) = 2.0 + 1 = 1
f(1) = 2.1 + 1 = 3f(1) = 2.1 + 1 = 3
Logo, temos que os pontos sãoLogo, temos que os pontos são (0,1)(0,1) ee (1,3)(1,3)
Dessa forma
garantimos que
esses pontos
pertencem à reta.
2º passo:2º passo: calcularcalcular oo valorvalor dede
yy para cada valor de xpara cada valor de x
escolhido.escolhido.

7. 3º passo:3º passo: marcarmarcar osos pontospontos no gráfico.no gráfico.
4º passo:4º passo: ligarligar osos pontospontos..
1
1
3
2
x
y

8. Tente fazer sozinho!Tente fazer sozinho!
Construa o gráfico da função:Construa o gráfico da função:
2
1−
=
x
y

9. SoluçãoSolução
1º passo: x = 3 e x = 51º passo: x = 3 e x = 5
2º passo: f(3) = 1 e f(5) = 22º passo: f(3) = 1 e f(5) = 2
3º e 4º passos:3º e 4º passos:
x
y
1
1
2
2 3 4 5

10. O que éO que é coeficientecoeficiente
angularangular??
É oÉ o valorvalor numériconumérico que multiplicaque multiplica aa
variávelvariável xx. Indica a. Indica a inclinação da retainclinação da reta
em relação ao eixo x.em relação ao eixo x.
Exemplo:Exemplo:
 y = 2x + 1y = 2x + 1  a = 2a = 2
 y = x – 5y = x – 5  a = 1a = 1
Ou seja, é o valor
de a na expressão:
y = ax + b.

11. O que éO que é coeficientecoeficiente
linearlinear??
É oÉ o valorvalor dede bb em y = ax + b. Indicaem y = ax + b. Indica
oo valor de yvalor de y, onde a reta do gráfico, onde a reta do gráfico
corta o eixo das ordenadascorta o eixo das ordenadas..
Exemplo:Exemplo:
 y = 2x + 1y = 2x + 1  b = 1b = 1
 y = x – 5y = x – 5  b = -5b = -5

12. O que éO que é ZeroZero dada
funçãofunção??
É oÉ o valor de xvalor de x onde aonde a reta do gráficoreta do gráfico
cortacorta o eixo daso eixo das abscissasabscissas..
Exemplos:Exemplos:
 y = 2x + 1y = 2x + 1  0 = 2x + 10 = 2x + 1  x = -1/2x = -1/2
 y = x – 5y = x – 5  0 = x – 50 = x – 5  x = 5x = 5
Ou seja, o valor de x para y = 0.

13. Zero da função
0 = 2x-1
x = 1/2
f(x) = 2x – 1
f(0) = 2.0 -1 = -1
f(1) = 2.1 – 1 = 1
f(2) = 2.2 – 1 = 3
Coeficiente angular
x
y
1
1
2
2 3 4 5-1
-1
3
Coeficiente
linear
Coeficiente linear

14. Tente fazer sozinho!Tente fazer sozinho!
I) Encontre y = f(x) sendo f uma funçãoI) Encontre y = f(x) sendo f uma função
polinomial do 1º grau, sabendo que f(-6) = 8polinomial do 1º grau, sabendo que f(-6) = 8
e f(6) = 12.e f(6) = 12.
II) Seja f uma função real definida pela leiII) Seja f uma função real definida pela lei
f(x) = ax – 3. Se 3 é raiz da função, qual éf(x) = ax – 3. Se 3 é raiz da função, qual é
o valor de f(10)?o valor de f(10)?

15. III) (UF-AM) A função f definida porIII) (UF-AM) A função f definida por
f(x) = -3x +m está representada abaixo:f(x) = -3x +m está representada abaixo:
Então o valor deEntão o valor de é:é:
)0(
)1()2(
f
ff +
x
y
1
5
7
7
5
−

16. SoluçõesSoluções
I) f(-6) = 8 e f(6) = 12I) f(-6) = 8 e f(6) = 12
y = ax + by = ax + b



+=
+−=
ba
ba
612
68
20 = 2b20 = 2b
b = 10b = 10
8 = -6a + 108 = -6a + 10
-2 = -6a-2 = -6a
a = 1/3a = 1/3
Logo, f(x) = 1/3 x + 10

17. II) f(x) = ax - 3II) f(x) = ax - 3
f(3) = 3a - 3 = 0f(3) = 3a - 3 = 0
3a = 33a = 3
a = 1a = 1
f(x) = x – 3f(x) = x – 3
f(10) = 10 – 3f(10) = 10 – 3
f(10) = 7f(10) = 7

18. III) f(x) = -3x + mIII) f(x) = -3x + m
f(1) = -3.1 + m = 0f(1) = -3.1 + m = 0
-3 + m = 0-3 + m = 0  m = 3m = 3
f(x) = -3x + 3f(x) = -3x + 3
f(0) = -3.0 + 3 = 3f(0) = -3.0 + 3 = 3
f(1) = -3.1 + 3 = 0f(1) = -3.1 + 3 = 0
f(2) = -3.2 + 3 = -3f(2) = -3.2 + 3 = -3
1
3
03
)0(
)1()2(
−=
+−
=
+
f
ff

19. Como identificamos se uma funçãoComo identificamos se uma função
éé crescentecrescente ouou decrescentedecrescente??
Verificando o sinal do a em y=ax+b. SeVerificando o sinal do a em y=ax+b. Se aa
forfor negativonegativo, então a função é, então a função é decrescentedecrescente..
SeSe aa forfor positivopositivo, então a função é, então a função é crescentecrescente..
Exemplos:Exemplos:
 y = -x + 2y = -x + 2  a = -1a = -1  função decrescentefunção decrescente
 Y = ½ + 4Y = ½ + 4  a = ½a = ½  função crescentefunção crescente

20. Também podemos fazer aTambém podemos fazer a
análise gráfica:análise gráfica:
x
y
x
y
FunçãoFunção
decrescentedecrescente
FunçãoFunção
crescentecrescente

21. Como resolvemosComo resolvemos sistemassistemas
através deatravés de gráficosgráficos??
BastaBasta traçartraçar osos gráficosgráficos das duasdas duas
equações, noequações, no mesmo planomesmo plano cartesiano. Ocartesiano. O
resultadoresultado é o ponto deé o ponto de interseçãointerseção..
Exemplo:Exemplo:
Pontos da 1ª equação: (1,4) e (3,2)Pontos da 1ª equação: (1,4) e (3,2)
Pontos da 2ª equação: (0,2) e (-2,1)Pontos da 2ª equação: (0,2) e (-2,1)



=+−
=+
42
5
yx
yx

22. Logo, S = (2,3)
x
y
1
1
2
2 3 4 5-1
-1
3
4
-2
-2
I = (2,3)

23. Como é feito oComo é feito o estudoestudo
do sinaldo sinal de uma função?de uma função?
Seguindo os passos:Seguindo os passos:
1º passo:1º passo: LocalizarLocalizar oo zero da funçãozero da função nana
reta real.reta real.
2º passo:2º passo: traçartraçar aa retareta do gráfico.do gráfico.
3º passo:3º passo: analisamosanalisamos osos intervalosintervalos onde aonde a
função éfunção é positivapositiva ouou negativanegativa..

24. Exemplo: y = x - 2Exemplo: y = x - 2
1º passo: x – 2 = 01º passo: x – 2 = 0  x = 2x = 2
2º passo: função crescente2º passo: função crescente
3º passo: y < 0, para x < 23º passo: y < 0, para x < 2
y = 0, para x = 2y = 0, para x = 2
x
2

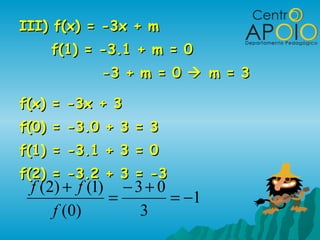
25. Como resolvemos umaComo resolvemos uma
inequaçãoinequação do 1º grau?do 1º grau?
Fazendo oFazendo o estudo do sinalestudo do sinal..
Exemplo: 2x – 7 > 0Exemplo: 2x – 7 > 0
 zero da função: 2x – 7 = 0zero da função: 2x – 7 = 0  x = 7/2x = 7/2
 a > 0a > 0  função crescentefunção crescente
Resposta:Resposta:
x
7/2
] [+∞,
2
7

26. E se for umaE se for uma inequaçãoinequação
produtoproduto ou umaou uma
inequação quocienteinequação quociente??
Se for umaSe for uma inequação produtoinequação produto devemosdevemos
fazer ofazer o estudo do sinalestudo do sinal dede cada fatorcada fator. Se. Se
forfor inequação quocienteinequação quociente, devemos fazer o, devemos fazer o
estudo do sinalestudo do sinal dodo dividendodividendo e doe do divisordivisor,,
separadamente.separadamente.

27. Exemplos:Exemplos:
I) (x-2) (1-2x) ≥ 0I) (x-2) (1-2x) ≥ 0
x – 2 = 0x – 2 = 0  x = 2x = 2 e 1 – 2x = 0e 1 – 2x = 0  x = ½x = ½
x
1/2
x
2
x
21/2
+++ --------------------------
----------------------- +++++
-+-
S = [1/2 , 2]

28. II)II)
x + 3 = 0x + 3 = 0  x = -3 e x – 1 = 0x = -3 e x – 1 = 0  x = 1x = 1
1,0
1
3
≠>
−
+
x
x
x
+++++++++++++--------
x
-3
x
1
++++++--------------------
1
x
-3
+-+
S=]-∞,-3[ U ]1,+ ∞[

29. Tente fazer sozinho!Tente fazer sozinho!
(UFC-CE) O conjunto solução, nos números(UFC-CE) O conjunto solução, nos números
reais, da inequaçãoreais, da inequação é igual a:é igual a:1
1
1
−>
+
−
x
x
{ }
{ }
{ }
{ }
{ }3;)
2;)
1;)
0;)
1;)
>∈
>∈
>∈
>∈
−>∈
xRxe
xRxd
xRxc
xRxb
xRxa

30. SoluçãoSolução
0
1
2
0
1
11
01
1
1
1
1
1
>
+
⇒>
+
++−
⇒>+
+
−
⇒−>
+
−
xx
xx
x
x
x
x
1 + x = 0 x = -1
++++++++++++---------
x
-1
S=]-1,+ ∞[
letra A