Explorando a ideia da função

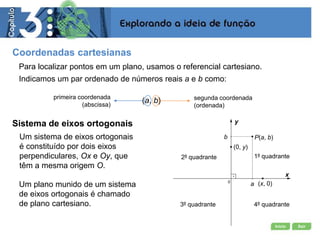
Início Sair
Coordenadas cartesianas
Para localizar pontos em um plano, usamos o referencial cartesiano.
Indicamos um par ordenado de números reais a e b como:
(a, b)primeira coordenada
(abscissa)
segunda coordenada
(ordenada)
Sistema de eixos ortogonais
Um sistema de eixos ortogonais
é constituído por dois eixos
perpendiculares, Ox e Oy, que
têm a mesma origem O.
Um plano munido de um sistema
de eixos ortogonais é chamado
de plano cartesiano.
P(a, b)
y
x
(0, y)
1º quadrante2º quadrante
3º quadrante 4º quadrante
(x, 0)
b
a

Início SairCapítulo 3 • Explorando a ideia de função
x
1 2 3 4‒4 ‒3 ‒2 ‒1
4
3
2
1
‒1
‒2
‒3
0
B
Cada par ordenado de números reais corresponde a um ponto do plano
cartesiano e, reciprocamente, a cada ponto do plano corresponde um par
ordenado de números reais.
Vamos localizar no plano cartesiano abaixo os pontos:
A(4, 1)
B(1, 4)
C(‒2, ‒3)
D(2, ‒2)
E(‒1, 0)
F(0, 3)
O(0, 0)
y
OE
C
D
A
F

Explorando intuitivamente a noção de função
A ideia de função está presente quando relacionamos duas
grandezas variáveis.
Exemplo
Número de litros Preço a pagar (R$)
1 2,90
2 5,80
3 8,70
4 11,60
40 116,00
x 2,90x
MM
O preço a pagar é dado
em função do número de
litros comprados, ou seja,
o preço a pagar depende
do número de litros
comprados.
O preço (p) a pagar é igual a 2,60 vezes o número de litros comprados.
p = 2,60x
Relação entre o número de litros
de gasolina e o preço a pagar

Observe os conjuntos A e B. Devemos associar cada elemento de A
a seu triplo em B.
Todos os elementos de A têm
correspondentes em B.
Cada elemento de A corresponde
a um único elemento de B.
A noção de função por meio de conjuntos
‒2 •
‒1 •
0 •
1 •
2 •
• ‒8
• ‒6
• ‒4
• ‒3
• 0
• 3
• 6
• 7
A B
Temos uma função de A em B, expressa pela função y = 3x.

Observe esses conjuntos.
Não é uma função de A em B,
pois ao elemento 0 de A
correspondem 3 elementos de B.
Não é uma função de A em B,
pois há elementos de A que não
têm correspondentes em B.
Cada elemento de A é menor do
que um elemento de B.
Cada elemento de A tem o mesmo
valor que um elemento de B.
0 •
4 •
• 2
• 3
• 5
A B
‒4 •
‒2 •
0 •
2 •
4 •
• 0
• 2
• 4
• 6
• 8
A B

Todos os elementos de A têm
correspondente em B.
Cada elemento de A corresponde a
um único elemento de B.
A correspondência entre A e B é dada pela fórmula y = x4.
Portanto, essa correspondência é uma função de A em B.
‒2 •
‒1 •
0 •
1 •
2 •
• 0
• 1
• 4
• 8
• 16
A B

Definição e notação
Usamos a seguinte notação:
Lê-se: f é uma função de A em B.
A função f transforma x de A em y de B.
y = f(x) Lê-se: y é igual a f de x.
x • • y
f
Dados dois conjuntos não vazios A e B, uma função de A em B é uma regra
que indica como associar cada elemento x A a um único elemento y B.
f: A B ou A Bf
A B

Domínio, contradomínio e conjunto imagem de uma função
Dada uma função f de A em B.
O conjunto A chama-se
domínio (D) da função.
O conjunto B chama-se
contradomínio (CD) da função.
Para cada x de A, o elemento y
de B chama-se imagem de x
pela função f.
O conjunto de todos os y é
chamado conjunto imagem da
função f e é indicado como Im(f).
x • • y
f
A B

Gráficos de funções
O gráfico de uma função ajuda a analisar a variação de grandezas, uma
dependendo da outra.
Construção de gráficos de funções
Vamos construir o gráfico de uma função.
• Construir uma tabela com valores x escolhidos convenientemente e seus
respectivos correspondentes y.
• A cada par ordenado (x, y) da tabela, associar um ponto do plano
determinado pelos eixos x e y.
• Marcar um número suficiente de pontos até que seja possível esboçar o
gráfico da função.

Exemplo
Função y = 2x + 1, com x real.
Como x varia no conjunto dos números
reais, escolhemos alguns valores
arbitrários para x e obtemos os valores
correspondentes para y.
Com os pares ordenados (x, y) obtidos,
podemos localizá-los no plano cartesiano.
x y = 2x + 1 (x, y)
‒2 ‒3 (‒2, ‒3)
‒1 ‒1 (‒1, ‒1)
0 1 (0, 1)
1 3 (1, 3)
2 5 (2, 5)
Unindo os pontos, obtemos a reta que
representa a função y = 2x + 1.
y
x
y = 2x +15
3
1
1 2
‒1
‒3
‒1‒2 0
‒2

Reconhecendo se um gráfico é de uma função
Para uma função existir, é necessário que, para qualquer x de um conjunto de
valores, corresponda um único y, de outro ou do mesmo conjunto de valores.
Geometricamente, isso significa que, no gráfico de uma função, qualquer reta
perpendicular ao eixo x deve intersectar o gráfico sempre em um único ponto.
Exemplos
É uma função. Não é uma função.
É uma função somente
para 1 ≤ x ≤ 4.

Função afim
Definição de função afim
Exemplos
y = ‒x + 6
y = 4x
a = ‒1 e b = 6
a = 4 e b = 0
y = 2x ‒ 7
a = 2 e b = ‒7
Função afim é toda função de em cuja lei de formação pode ser indicada
por y = ax + b, com a e b reais.
O gráfico de uma função afim
O gráfico de uma função afim é sempre uma reta não perpendicular ao eixo x.
Como dois pontos determinam uma reta, basta encontrar apenas dois de seus
pontos para traçá-la.

Exemplo
x y = 5x ‒ 6
1 ‒1
2 4
O gráfico “corta” o eixo y no ponto (0, ‒6), pois para:
y
x
y = 5x ‒ 6
1
1
4
2
‒1
‒4
O gráfico (a reta) “corta” o eixo x no ponto ,
pois para:
y = 0 5x – 6 = 0 x =
x = 0 y = 5 . 0 ‒ 6 y = ‒ 6

Ângulo de declividade da reta de uma função afim
O ângulo correspondente a um giro no sentido anti-horário, partindo do eixo x
até a reta que corresponde ao gráfico de uma função afim, é chamado de
ângulo de declividade da reta.
• Quando a é positivo em y = ax + b, é um ângulo agudo e a função afim é
crescente.
y
x
y
x
• Quando a é negativo, é um ângulo obtuso e a função afim é decrescente.

Um caso particular de função afim: a função linear
y = 3x y = 2x + 5
É função afim que é função linear. É função afim mas não é função linear.
O gráfico de uma função linear também é uma
reta mas com uma característica própria: a reta
passa pela origem (0, 0).
Gráfico de uma função linear
Uma função, definida em e com valores em , com lei de formação do tipo
y = ax, com a real e a 0, é chamada de função linear.
A função linear é um caso particular da função afim, pois y = ax equivale a
y = ax + b, com a 0 e b = 0.
y = 2x
y
x
Exemplo

Função identidade
A função linear que faz corresponder a cada x (real) um y tal que y = x
é chamada de função identidade.
Ou seja, cada número real corresponde a ele próprio.
Função linear e proporcionalidade
As funções do tipo y = ax, com a 0, x e y reais, apresentam proporcionalidade
direta entre os valores de x e y.
y
y = x
x
1º quadrante
2º quadrante
3º quadrante
4º quadrante
CASADETIPOS/ARQUIVODAEDITORA

Estudo do sinal da função afim
Fazer um estudo sobre o sinal de uma função afim consiste em determinar os
valores de x do domínio para os quais f(x) = 0, f(x) > 0 e f(x) < 0.
Zero da função afim
Para determinar esse valor, basta resolver a equação ax + b = 0.
Geometricamente, o zero da função afim é a abscissa do ponto de intersecção
do gráfico da função com o eixo x.
O valor de x para o qual a função f(x) = ax + b, a 0, se anula, ou seja, para
o qual f(x) = 0, denomina-se zero da função afim.
f(x) = 0 ax + b = 0 ax = ‒b x = ‒
O coeficiente b em y = ax + b
Na função afim y = ax + b, para x = 0, temos que y = b, ou seja, b é o valor da
função quando x = 0.
O gráfico intersecta o eixo y no ponto de ordenada b.

Estudo do sinal da função pela análise do gráfico
a < 0 (função crescente) a < 0 (função decrescente)
Dispositivo prático:
x
+
‒r
Dispositivo prático:
x
+
‒ r
y
x
(r, 0)
imagens
positivas
imagens
negativas
x
y
(r, 0)
imagens
positivas
imagens
negativas
x = r f(x) = 0
x > r f(x) > 0
x < r f(x) < 0
x = r f(x) = 0
x > r f(x) < 0
x < r f(x) > 0

Resolução de inequações do 1o grau
Você já viu esse conteúdo. Vamos relembrar com um exemplo.
Podemos também resolver por meio do estudo do sinal da função afim:
S = x | x >
2x – 5 > 0, em
f(x)
x > f(x) > 0
S = x | x >
x+
‒
2x ‒ 5 > 0 em
2x > 5 x >
2x – 5 = 0 2x = 5 x = (zero)

Função quadrática
Definição de função quadrática
Exemplos
y = 3x2 ‒ 2x + 5 y = ‒x2 + 5x + 6
a = 3, b = ‒2 e c = 5 a = ‒1, b = 5 e c = 6
y = ‒4x2 ‒ 3x
a = ‒4, b = ‒3 e c = 0
y = ‒6x2
a = ‒6, b = 0 e c = 0
Função quadrática é toda função de em cuja lei de formação pode
ser indicada por y = ax2 + bx + c, com a, b e c reais e a 0.

Valor de uma função quadrática em um ponto
Dada uma função y = ax2 + bx + c, pode-se ter um valor de x e determinar
o valor de y ou ter um valor de y e determinar o valor de x.
Exemplo
Dado x = 2, vamos calcular o valor de y.
y = 22 – 5 . 2 + 6
y = 4 – 10 + 6
y = 0
Então, para x = 2, y = 0.
Considere a função y = x2 ‒ 5x + 6.
Dado y = 0, vamos calcular x.
0 = x2 – 5 . x + 6
x2 – 5x + 6 = 0
Resolvendo a equação do 2º grau,
temos que x′ = 3 e x″ = 2.
Então, para y = 0, x = 3 ou x = 2.

Zeros de uma função quadrática
Exemplo
Considere a função y = x2 ‒ 9x + 20.
Fazemos y = 0 e determinamos os valores reais de x que satisfazem a
equação do 2º grau obtida.
x = = =
x′ = 5
x″ = 4
Damos o nome de zeros de uma função quadrática dada por y = ax2 + bx + c
(a 0), aos valores reais de x que anulam y, quando existirem.
= b2 ‒ 4ac = (‒9)2 ‒ 4 . 1 . 20 = 81 – 80 = 1
Os zeros da função quadrática y = x2 ‒ 9x + 20 são 5 e 4.

Gráfico de uma função quadrática
x 4 3 2 1 0 ‒1 ‒2
y 5 0 ‒3 ‒4 ‒3 0 5
Exemplo
• A parábola apresenta simetria.
• O eixo de simetria da parábola é
sempre perpendicular ao eixo x.
• O encontro da parábola com o
seu eixo de simetria é o vértice
da parábola.
O gráfico de uma função quadrática, ou seja, com y igual a um polinômio
do 2º grau da forma ax2 + bx + c, com a 0, é sempre uma curva chamada
parábola.
eixo de simetria
x
y
0
V(1, ‒4) vértice da parábola
= = = 1

Gráfico da função quadrática e os coeficientes a, b, c
Responsável pela concavidade e abertura da parábola.
• Se a > 0, a concavidade é para cima.
Coeficiente a
• Se a < 0, a concavidade é para baixo.
Quanto maior o valor absoluto de a, menor será a abertura da parábola,
independentemente da concavidade.
x
a > 0
y y = 5x2
y = 2x2
y = x2
0
y = x2
y = x2
a < 0
x
y = ‒5x2 y = ‒2x2
y = ‒x2
0
y
y = ‒ x2
y = ‒ x2

Indica se a parábola cruza o eixo y no ramo crescente ou decrescente da
parábola, no sentido da esquerda para a direita.
• Se b > 0, a parábola cruza o
eixo y no ramo crescente.
Coeficiente b
• Se b < 0, a parábola cruza o
eixo y no ramo decrescente.
• Se b = 0, a parábola cruza o eixo y no vértice.
x
y
x
y
x
y
x
y
x
y
x
y

Indica o ponto em que a parábola cruza o eixo y.
A parábola cruza o eixo y no ponto (0, c).
Coeficiente c
A parábola e suas intersecções com os eixos
Dada a equação y = x2 – 2x + 1, vejamos como calcular
algebricamente os pontos de intersecção com os eixos.
• Intersecção com eixo y:
A parábola intersecta o eixo y em (0,1).
• Intersecção com eixo x:
x
y
c
x
y
(1, 0)
(0, 1)
x = 0 y = 02 – 2 . 0 + 1 y = 1
y = 0 x2 – 2x + 1
x = = 1
= 4 – 4 = 0 = 0

V – , – = V(2, ‒8)
Vértice da parábola, valor máximo ou valor mínimo da função quadrática
Exemplo
Dada a equação y = 2x2 – 8x, vamos calcular o vértice da parábola.
A função quadrática y = 2x2 – 8x assume valor mínimo –8 quando x = 2.
Todos os valores da função
são maiores do que –8.
O vértice de uma parábola dada por y = ax2 + bx + c (a 0) é determinado por:
V – , –
= b2 – 4ac = (–8)2 – 4 . 2 . 0 = 64

Estudo do sinal da função quadrática
Estudar o sinal da função quadrática significa determinar os valores reais de x
para os quais: f(x) = 0, f(x) > 0 e f(x) < 0.
• a função admite dois zeros reais diferentes, x′ e x″;
• a parábola que representa a função intersecta o eixo x em dois pontos.
a > 0 a < 0
f(x) = 0 para x = x″ ou x = x′
f(x) > 0 para x < x″ ou x > x′
f(x) < 0 para x″ < x < x′
f(x) = 0 para x = x″ ou x = x′
f(x) > 0 para x″ < x < x′
f(x) < 0 para x < x″ ou x > x′
1º caso: > 0
+
––
x’x”+ +
– x’x”
Assim, quando > 0, f(x) tem sinal oposto ao de a quando x está entre as raízes
da equação, e tem o sinal de a quando x está fora do intervalo das raízes.

• a função admite um zero real duplo x′ = x″;
• a parábola que representa a função tangencia o eixo x.
a > 0 a < 0
f(x) = 0 para x = x′ = x″ f(x) = 0 para x = x′ = x″
2º caso: = 0
f(x) > 0 para x x′ f(x) < 0 para x x′
+ +
x’ = x”
– –
x’ = x”
Assim, quando = 0, f(x) tem o sinal de a para x diferente da raiz da equação.

• a função não admite zeros reais;
• a parábola que representa a função não intersecta o eixo x.
f(x) > 0 para todo x real f(x) < 0 para todo x real
3º caso: < 0
Assim, quando < 0, f(x) tem o sinal de a para qualquer valor real de x.
a > 0
+ + + + + + + + +
a < 0
– – – – – – – – –

Desigualdades como:
x2 – 5x + 6 > 0 3x2 < 0 (x ‒ 3)(x + 3) < 0
são denominadas inequações do 2º grau.
Vamos resolver a inequação x2 – 3x + 2 < 0.
Isso significa determinar os
valores reais de x para os quais
a função f(x) = x2 – 3x + 2
assume valores negativos.a = 1 > 0; a > 0
As raízes da equação x2 – 3x + 2 são
x′ = 1 e x″ = 2.
–
++
1 2
x
Como queremos f(x) < 0 então
S = {x | 1 < x < 2}.
= (–3)² – 4 . 1 . 2 = 9 – 8 = 1 > 0 = 0
Inequações de 2o grau
Exemplo

Explorando a ideia da função

Recomendados

Recomendados

Mais conteúdo relacionado

Mais procurados

Mais procurados (20)

Semelhante a Explorando a ideia da função

Semelhante a Explorando a ideia da função (20)

Mais de Antonio Magno Ferreira

Mais de Antonio Magno Ferreira (8)

Último

Último (20)

Explorando a ideia da função