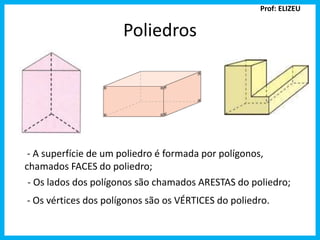
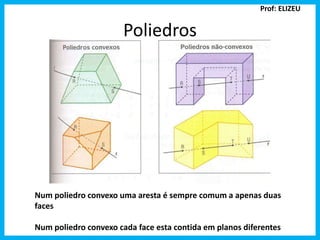
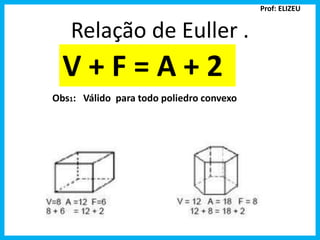
O documento discute poliedros, definindo suas faces, arestas e vértices. Também apresenta a fórmula de Euler para poliedros convexos e exemplos de cálculo de vértices e arestas. Finalmente, lista os cinco poliedros regulares de Platão.

1. Geometria Espacial
Poliedros
Prof: ELIZEU

2. - A superfície de um poliedro é formada por polígonos,
chamados FACES do poliedro;
- Os lados dos polígonos são chamados ARESTAS do poliedro;
- Os vértices dos polígonos são os VÉRTICES do poliedro.
Poliedros
Prof: ELIZEU

3. Poliedros
Num poliedro convexo uma aresta é sempre comum a apenas duas
faces
Num poliedro convexo cada face esta contida em planos diferentes
Prof: ELIZEU

4. Relação de Euller .
V + F = A + 2
Obs1: Válido para todo poliedro convexo
Prof: ELIZEU

5. Ex2: Um poliedro convexo possui exatamente 4 faces
pentagonais e 6 faces triangulares. Determine o número
de vértices desse sólido.
Ex1: Um poliedro convexo possui 12 faces e 8 vértices.
Determine o número de arestas desse poliedro.
Prof: ELIZEU

6. Existem apenas cinco poliedros de Platão:
- Tetraedro;
- Hexaedro;
-Octaedro;
-Dodecaedro;
-Icosaedro.
Obs2: Se um poliedro convexo possui todas as faces formadas por
polígonos regulares e congruentes, então ele é chamado de
POLIEDRO REGULAR.
Poliedros de Platão
Prof: ELIZEU