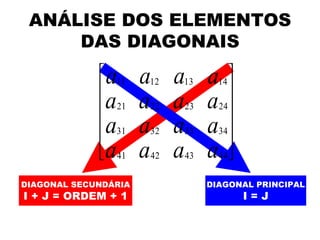
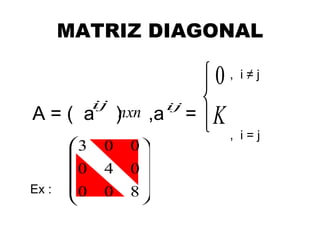
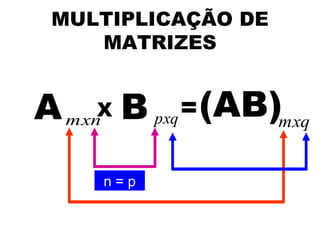
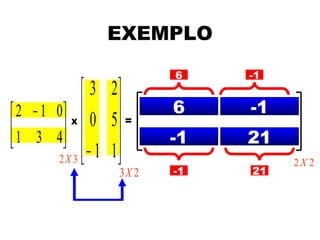
O documento descreve os conceitos básicos de matrizes, incluindo suas definições, tipos especiais como matrizes quadradas, diagonais e identidade. Também apresenta operações com matrizes como adição, subtração e multiplicação, além de propriedades dessas operações. Por fim, explica o conceito de determinante de matrizes.

1. MATRIZ

2. DEFINIÇÃO
TABELA RETANGULAR ONDE OS
ELEMENTOS ESTÃO DISPOSTOS
EM m LINHAS E n COLUNAS.
[ ] LINHAS
mxn ORDEM
COLUNAS

3. ELEMENTO GENÉRICO
aij COLUNA
LINHA
ELEMENTO

4. MATRIZ GENÉRICA
A=( a ij )mxn

5. MATRIZES
ESPECIAIS

6. MATRIZ LINHA
A = ( a ij )1xn
Ex : (1 5 8 )

7. MATRIZ COLUNA
A = ( a ij ) nx1
−2 
 
Ex :  4 
 7 
 

8. MATRIZ QUADRADA
A = ( a ij )nxn ordem n
− 2 9 0
 
 4 −6 7
 −8 10 
4

DIAGONAL DIAGONAL
SECUNDÁRIA PRINCIPAL

9. ANÁLISE DOS ELEMENTOS
DAS DIAGONAIS
 a11 a
12 a
13 a 14

 
 a21 a
22 a
23 a 24
a a a a 
 31 32 33 34

 a41
 a
42 a
43 a 44
DIAGONAL SECUNDÁRIA DIAGONAL PRINCIPAL
I + J = ORDEM + 1 I=J

10. MATRIZ DIAGONAL
 0 , i≠j
A=(
ij 
a )nxn ,a = K
ij
 , i=j
3 0 0
 
0 4 0
Ex : 0 0 8
 

11. MATRIZ IDENTIDADE
0, i≠j
I n= ( a ij )
nxn
, a ij
=
1,i=j
1 0 0
1 0 0 1 0
I =  I 3= 
2
0 1  
0 0 1
 

12. MATRIZ TRANSPOSTA
t
A = ( a ij) A = ( a ji )
mxn nxm
 − 3 1
  t  − 3 4 0
Ex : A=  4 7 A= 
 1 7 5 
 0 5  
 

13. MATRIZ SIMÉTRICA
A =( aij)nxn , com a ij = a ji
7 −3
-3 4
4
  t
Ex :
−3
 -3 8 −5
-5  A=A
 4 −5 
 4 -5 9

14. MATRIZ OPOSTA
A=( a ij )
mxn
-A = (- a ij )
mxn
 −1 7   1 − 7
   
A =  5 − 3 -A =  − 5 3 
2 9  − 2 − 9
   

15. MATRIZ ANTI-SIMÉTRICA
a
A = ( ij )
nxn
, com a ij = - a ji
 0 −2
-2 6
6
2 0  t
A= 2 -4
− 4 A = -A
− 6 4
 -6 4 0

DIAGONAL PRINCIPAL NULA

17. OPERAÇÕES
COM
MATRIZES

18. ADIÇÃO E SUBTRAÇÃO
Seja A = ( a
ij) mxn e B = (
mesma ordem.
b ) mxn duas matrizes de
ij
-
A+B
 a11   b11
a12    +
b12  a11 - b11 
 a +b
-
12 12

 a 21 a22 + b21
- b22 =  a21 +- b21 a +- b
22 22
a  b
a32  31   +
b32  a31 - b31 
 31 a +- b
32 32 

19. MULTIPLICAÇÃO DE
MATRIZES
A mxnX B pxq = (AB)mxq
n=p

20. EXEMPLO
6 -1
3 2
 2 − 1 0  0 = 6 -1
(2)(3)+(-1)(0)+(0)(-1) (2)(2)+(-1)(5)+(0)(1)
 1 3 4 
X 5
  -1
(1)(3)+(3)(0)+(4)(-1)
21
(1)(2)+(3)(5)+(4)(1)
2X 3
 − 1 1 2X 2
3X 2 -1 21

21. PROPRIEDADES DAS
OPERAÇÕES
-AxB≠BxA
t t t
- A x B = (B x A)
t t t
-A+B =(A+B)
-AxI=IxA=A

24. DETERMINANTE

25. DEFINIÇÃO
Número associado a uma matriz
quadrada .

26. ORDEM 2
 a c
A=  
 d b
a c
det(A) = = a.b – c.d
d b
DS DP

27. ORDEM 3
a b c
A= d 
e z

g
 h i

- - -
a b c a b
det(A) = d e z d e = ( aei +bzg + cdh ) – ( gec + hza + idb )
g h i g h
+ + +