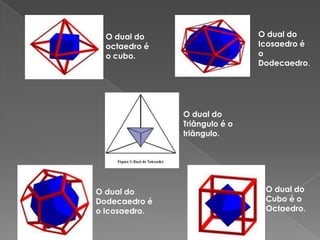
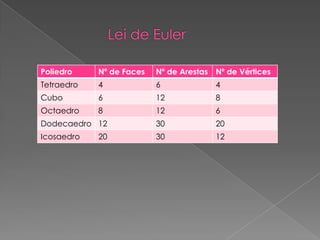
Um poliedro é um sólido geométrico com várias faces planas. Pode ser regular, com faces e ângulos iguais, ou irregular. Existem também sólidos não poliédricos limitados por superfícies curvas. Os poliedros regulares incluem os sólidos platônicos e os poliedros de Kepler-Poinsot.

2.  Poliedro: é um sólido geométrico cuja superfície é composta por
um número finito de faces, em que cada uma das faces é um
poligono.
 Trata-se de um objeto com muitas faces. Um poliedro tem "bicos",
que são os ângulos poliédricos, e faces planas, que são os
polígonos.
 Um poliedro que tenha como faces apenas polígonos regulares,
todos idênticos, e que também apresente todos os bicos (ângulos
poliédricos) idênticos entre si é um poliedro regular.
 Os poliedros podem ser Convexos ou Côncavos. Os poliedros são
convexos quando se encontram todos para o mesmo lado em
relação ao plano de qualquer uma das suas faces, ou seja, quando
as suas faces deixam sempre as demais no mesmo semiespaço.
Caso contrário, os poliedros dizem-se côncavos

3.  Os sólidos limitados, no todo ou em parte, por superfícies curvas
chamam-se Não Poliedros. De entre estes são particularmente
importantes os Sólidos de Revolução. São sólidos de revolução o
cilindro, o cone e a esfera.
 Sólidos limitados só por superfícies curvas ou por superfícies planas e
curvas. Ex. cone, cilindro, esfera, ...


5.  Existem 9 poliedros regulares que são os 5 Sólidos Platónicos e os 4
Poliedros de Kepler-Poinsot.
 Trata-se de um objecto com muitas faces. Um poliedro tem "bicos",
que são os ângulos poliédricos, e faces planas, que são os
polígonos.
 Um poliedro que tenha como faces apenas polígonos regulares,
todos idênticos, e que também apresente todos os bicos (ângulos
poliédricos) idênticos entre si é um poliedro regular.

6.  Chama-se dual de um poliedro ao poliedro que se obtém unindo
por segmentos de recta os centros das faces consecutivas do
primeiro, ou seja, ao poliedro formado por dois poliedros, um dentro
do outro, de modo que os vértices do sólido interior coincidam com
o centro das faces do sólido exterior.
 Em geometria, os poliedros estão associados aos pares, chamados
duais, onde os vértices de um inscrevem às faces do outro.
 O dual do dual é o poliedro original. O dual de um poliedro com
vértices equivalentes é um com faces equivalentes, e de um com
arestas equivalentes é outro com arestas equivalentes.
 Assim os poliedros regulares — os Sólidos Platónicos e os Poliedros
de Kepler-Poinsot — estão organizados em pares de duais.

7. O dual do O dual do
octaedro é Icosaedro é
o cubo. o
Dodecaedro.
O dual do
Triângulo é o
triângulo.
O dual do O dual do
Dodecaedro é Cubo é o
o Icosaedro. Octaedro.

8. Poliedro Nº de Faces Nº de Arestas Nº de Vértices
Tetraedro 4 6 4
Cubo 6 12 8
Octaedro 8 12 6
Dodecaedro 12 30 20
Icosaedro 20 30 12

9.  Trabalho elaborado por : Pedro Moreira
 Pedro Silva