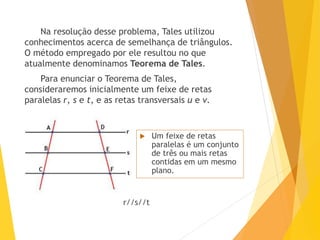
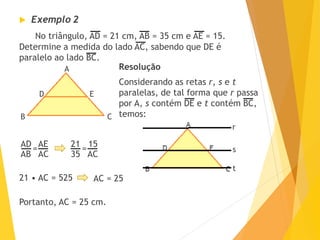
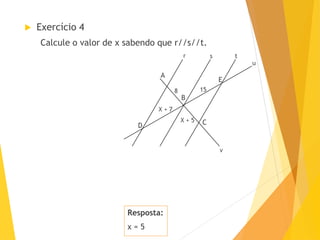
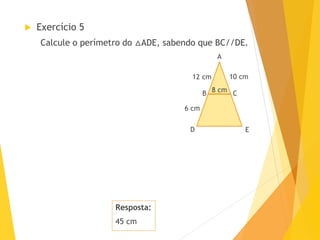
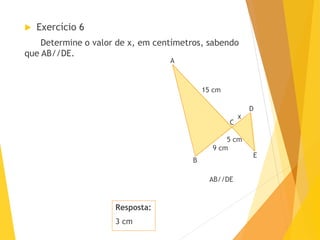
O documento apresenta o Teorema de Tales, que estabelece que a razão entre segmentos determinados em uma reta transversal é igual à razão entre os segmentos correspondentes na outra reta transversal, quando cortadas por um feixe de retas paralelas. Exemplos e exercícios ilustram a aplicação do teorema na resolução de problemas geométricos.

1. Seminário de Matemática
 Colégio João Paulo I
 Alunos: Caio Santos, Julia de Souza, Marcela Miranda, Milena
Muniz, Vitória Martins e Vitor Caetano
 Turma: 1002/Tarde
 Professor: João Belarmino
Teorema de Tales

2. Teorema de Tales
O grego Tales de Mileto, que viveu
por volta da primeira metade do século
VI a.C., é considerado o pai da
Geometria Demonstrativa, na qual se
faz necessário justificar, por meio de
demonstrações lógicas, os
conhecimentos geométricos. Os estudos
de Tales contribuíram em diversas áreas
do conhecimento, como a Matemática,
Tales de Mileto
Filosofia e Astronomia, tornando-o conhecido como um
dos sete sábios da Antiguidade.
Acredita-se que Tales tenha vivido parte de sua vida
no Egito, onde se deparou com um problema: calcular a
altura de uma pirâmide; e ao resolvê-lo, tornou-se
muito admirado.

3. Na resolução desse problema, Tales utilizou
conhecimentos acerca de semelhança de triângulos.
O método empregado por ele resultou no que
atualmente denominamos Teorema de Tales.
Para enunciar o Teorema de Tales,
consideraremos inicialmente um feixe de retas
paralelas r, s e t, e as retas transversais u e v.
 Um feixe de retas
paralelas é um conjunto
de três ou mais retas
contidas em um mesmo
plano.
r//s//t

4. Na figura, temos:
 A e D, B e E, C e F,
determinados nas
retas transversais
pela mesma reta
paralela,
denominados pontos
 correspondentes;
 AB e DE, BC e EF, AC e DF, determinados nas retas
transversais pelo mesmo par de retas paralelas,
denominados segmentos correspondentes.
De acordo com o Teorema de Tales:
Se duas retas transversais são cortadas por um feixe
de retas paralelas, então a razão entre quaisquer dois
segmentos determinados em uma das transversais é
igual à razão entre os segmentos correspondentes da
outra transversal.

5. Exemplos
 Exemplo 1
Na figura, AB = 3, BC = 9 e DE = 5. Determine o
valor EF, sabendo que as retas r, s e t são
paralelas.
Resolução
Pelo Teorema de Tales, temos:
AB
BC
DE
EF
=
3
9
5
EF
=
3 • EF = 45 EF = 15

6.  Exemplo 2
No triângulo, AD = 21 cm, AB = 35 cm e AE = 15.
Determine a medida do lado AC, sabendo que DE é
paralelo ao lado BC.
A
D
CB
E
Resolução
Considerando as retas r, s e t
paralelas, de tal forma que r passa
por A, s contém DE e t contém BC,
temos:
r
s
t
AD
AB
AE
AC
=
21
35
15
AC
=
21 • AC = 525 AC = 25
Portanto, AC = 25 cm.

7. Exercícios
 Exercício 1
Na figura, as retas r, s, t e u, paralelas entre si,
são cortadas por duas transversais que determinam os
pontos A, B, C, D, E , F, G, e H. r//s//t//u
Nessas condições, verifique quais
das igualdades estão incorretas.
AC
AB
EF
EG
=
AC
AD
EG
EH
=
AB
AC
EF
EG
=a) b) c)
EG
FH
BD
AC
=
AD
BD
EG
EH
=
BD
BC
FH
FG
=d) e) f)
BC
CD
FG
GH
=
GH
EF
AB
CD
=
EH
EF
AD
AB
=g) h) i)
Respostas:
e, c, f, h.

8. Resposta:
x = 6
 Exercício 2
Determine o valor de x.
x + 4
5
x + 2
4
u
s
t
r
v
r//s//t

9. Rua A
Resposta:
a = 30, b = 36, c = 54
 Exercício 3
O proprietário de uma área quer dividi-la em três
lotes, conforme a figura a seguir.
20 24 36
b
a
c
Sabendo-se que os laterais
dos terrenos são paralelas
e que a + b + c = 120 m, os
valores de a, b e c, em
metros, são:

10. Resposta:
x = 5
 Exercício 4
Calcule o valor de x sabendo que r//s//t.
B
D
E
C
15
X + 5
sr
X + 7
8
u
t
A
v

11. Resposta:
45 cm
 Exercício 5
Calcule o perímetro do △ADE, sabendo que BC//DE.
A
B
D E
C
6 cm
10 cm12 cm
8 cm

12. Resposta:
3 cm
 Exercício 6
Determine o valor de x, em centímetros, sabendo
que AB//DE.
A
B
D
E
C
9 cm
5 cm
AB//DE
x
15 cm

13. Fonte:
 Conceito: Livro Novo Olhar Matemática – Trigonometria
– Vol. 1 – Joamir Souza
 Exemplos: Livro Novo Olhar Matemática – Trigonometria
– Vol. 1 – Joamir Souza
 Exercícios: Livro Novo Olhar Matemática –
Trigonometria – Vol. 1 – Joamir Souza