Baixado 37 vezes
Carregado porPéricles Penuel
Diedros e triedros
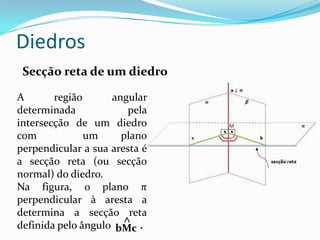
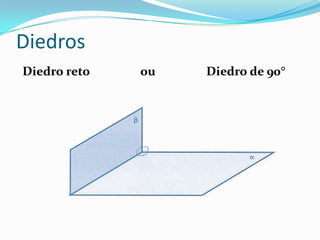
O documento apresenta os seguintes conceitos geométricos: 1) Diedros são formados pela interseção de dois planos e possuem faces, arestas e secção reta. 2) Triedros são formados pela interseção de três semi-retas não coplanares e determinam três semi-espaços. 3) Problemas envolvendo medidas de diedros e seus elementos são apresentados.
Diedros e triedros
- 1. MATEMÁTICA - 1 Ten Villa Nova CMCG - 2012
- 2. Objetivos •Identificar diedros eseus elementos. •Resolver problemas sobre diedros e seus elementos. •Identificar triedros •Identificar os elementos de um triedro. •Identificar angulóide (ou ângulo poliédrico) e seus elementos. •Resolver problemas sobre triedros e seus elementos.
- 3. Diedros Dois planos secantesα e β determinam no espaço quatro semi-espaços. Chama-se diedro à intersecção de dois desses semi-espaços. Na figura, os semiplanos α e β são as faces e a reta a é a aresta do diedro determinado pela intersecção dos semi- espaços I e I’.
- 4. Diedros Secção retade um diedro A região angular determinada pela intersecção de um diedro com um plano perpendicular a sua aresta é a secção reta (ou secção normal) do diedro. Na figura, o plano π perpendicular à aresta a determina a secção reta ^ definida pelo ângulo bMc .
- 5. Diedros Secção retade um diedro a) Todas as secções retas do mesmo diedro são congruentes. b) A medida de um diedro é a medida da sua secção reta. c) Dois diedros são congruentes quando suas secções retas são congruentes. d) Se o plano π não for perpendicular à aresta a, teremos simplesmente uma secção ou secção inclinada.
- 6. Diedros Diedro reto ou Diedro de 90°
- 7. Exercícios Dado diedro αȓβ,têm–se que as projeções ortogonais de um ponto A, A ∉ α e A ∉ β, sobre α e β respectivamente A’ e A’’. Sabendo que o ângulo A’ÂA’’ mede 80°, determine a medida do diedro.
- 8. Triedros → → → Dadas três semi-retas Va, Vb e Vc de mesma origem V e não coplanares, consideremos os semi- espaços I, II e III como segue: I com origem no plano (bc) e → contendo Va II com origem no plano (ac) e → contendo Vb III com origem no plano (ab) e → contendo Vc
- 9. Triedros Chama-se triedro determinadopor → → → Va, Vb e Vc à intersecção dos semi- espaços I, II e III. V(a; b; c) = I ∩ II ∩ III