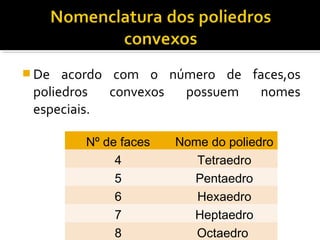
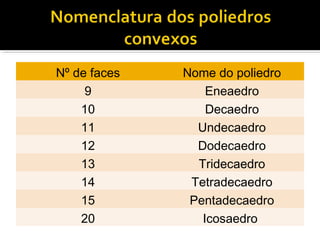
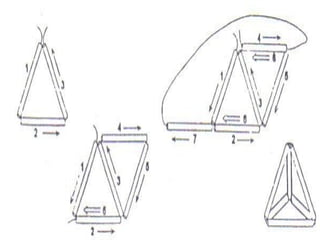
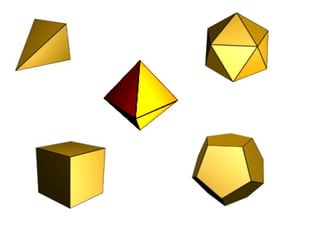
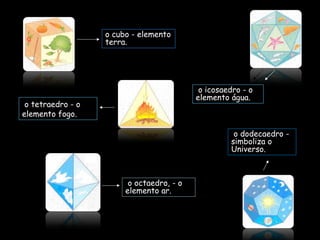
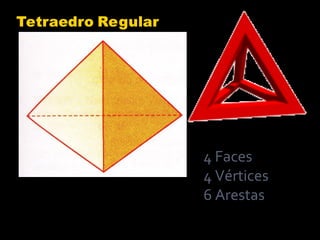
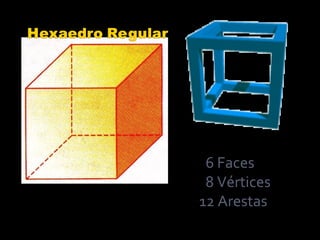
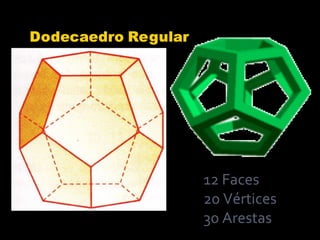
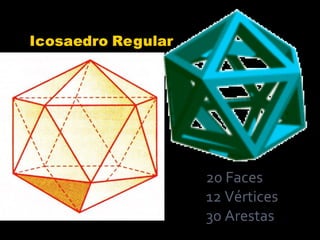
1) O documento discute a história e construção dos poliedros, figuras geométricas com quatro ou mais faces polígonais. 2) Platão foi o primeiro a demonstrar que existem apenas cinco poliedros regulares: cubo, tetraedro, octaedro, dodecaedro e icosaedro. 3) Cauchy provou posteriormente que existem nove poliedros regulares no total e não apenas cinco como acreditavam Platão e Pitágoras.

1. UM POUCO DA HISTÓRIA E CONSTRUÇÃO DOS POLIEDROS
Karla da Silva Pereira

4.  A Humanidade, na sua história, estudou a Matemática
em ordem inversa à que foi seguida nas suas escolas,
ou quase. De fato a numeração decimal é a primeira
coisa que se aprende, mal se vai à escola, e foi, pelo
contrário, uma tardia conquista de uma humanidade
já doutíssima em geometria. Poder-se-ia dizer que a
geometria é em vários milhares de anos mais velha do
que a Aritmética. Os gregos tinham um verdadeiro
culto pela geometria, que elevaram a um alto grau de
perfeição. Consideravam-na uma ciência que habitua
a raciocinar, que refina a inteligência; diziam pelo
contrário que não era preciso estudá-la com fins
práticos, mas para "a honra da mente Humana”.

5.  Platão (sec II a.C.9, o grande filósofo aluno de
Sócrates, foi o primeiro matemático a demonstrar
que existem apenas cinco poliedros regulares: o cubo,
tetraedro, octaedro dodecaedro e o icosaedro. Esses
poliedros são designados sólidos de Platão em virtude
do texto de platão sagundo o qual:
 “Um poliedro é regular quando as faces são
polígonos regulares congruentes,todas as arestas
são congruentes e todos os vértices são
congruentes.Isto significa que existe uma simetria
do poliedro que transforma cada face ,cada
aresta e cada vértice numa outra face,aresta ou
vértice.”

6.  Para Platão o universo era formado por um corpo e
uma alma ou inteligência. Na matéria havia porções
limitadas por triângulos, formando-se elementos que
diferem entre si pela natureza da forma das suas
superfícies periféricas. Se forem quadrados temos o
cubo- o elemento da terra. Se forem triângulos,
formando um tetraedro, teremos o fogo, cuja
natureza penetrante está simbolizada na agudeza dos
seus vértices.

7.  O ar é formado por octaedros e a água de isocaedros.
Platão admitia ainda que por intervenção inteligente,
uns se transformavam nos outros à excepção da terra,
que se transforma em si própria. O dodecaedro cheio
de harmonia simbolizava o próprio universo. No
entanto ainda existem dúvidas se o teorema" só há
cinco sólidos platónicos" se deve a Platão ou a
Pitágoras. Mas provar-se-ia mais tarde que este
teorema era falso e Cauchy provou que há nove
poliedros regulares e que não existem mais. O erro do
teorema de Platão ou de Pitágoras reside no fato de
os poliedros regulares por eles considerados não
serem obrigatoriamente convexos.

8. Associação dos Poliedros

9. o cubo - elementoo cubo - elemento
terra.terra.
o tetraedro - oo tetraedro - o
elemento fogo.elemento fogo.
o octaedro, - oo octaedro, - o
elemento ar.elemento ar.
o icosaedro - oo icosaedro - o
elemento água.elemento água.
o dodecaedro -o dodecaedro -
simboliza osimboliza o
Universo.Universo.

10.  É uma figura plana formada por uma linha
poligonal fechada.
 Do grego, poli quer dizer vários e gonos
significa ângulos.

11.  São sólidos geométricos com quatro ou mais
faces em forma de polígonos.
 Etmologicamente, poli quer dizer vários e a
terminação edro provém da palavra hedra,
que em grego significa face.
 Os bicos de um poliedro são ângulos
poliédricos formados por faces planas, que
são polígonos.

12.  Faces: são as figuras
planas que limitam o
sólido;
 Arestas: são os
segmentos de reta que
limitam as faces;
 Vértices: são os pontos
de encontro das
arestas.

13.  Ângulo Poliédrico é um conjunto de pontos do
espaço limitados por três ou mais ângulos
planos, não coplanares, em número finito, que
têm o mesmo vértice e, dois a dois, um lado
comum.
 Traduzindo isso para a linguagem menos formal
podemos dizer que, em se tratando de poliedros,
um ângulo sólido é o ângulo formado pelas faces
que chegam a um mesmo vértice.
 A medida de um ângulo poliédrico é dada pela
soma dos ângulos planos que delimitam este
ângulo sólido.

14.  Os ângulos poliédricos têm uma certa
propriedade: sua soma, por maior que seja o
número de faces que convergem para o
vértice em questão, é sempre menor do que
360°. Isto é, se chamarmos de A a soma dos
ângulos compreendidos entre as arestas de
um poliedro que chegam a um mesmo
vértice, temos que:
A < 360°

16. Cálculo do número de diagonais de um poliedro convexo
Soma dos ângulos internos de todas as faces de um poliedro
S = 360º. (V – 2)

17. DEMONSTRAÇÃO:
Sabemos que a soma dos ângulos internos de um polígono qualquer é dada
por S = 180º. (n – 2). Podemos aplicar essa fórmula a cada uma das F faces do
Poliedro. Vejamos:
S1 = 180º.(n1 – 2)
S2 = 180º.(n2 – 2)
...
SF = 180º.(nF – 2)
Somando todas as equações obtidas, teremos:
Sif = 180º.(n1 + n2 + ....+ nF) – 360º. F
Sif = 180º. 2A – 360º. F = 360º. (A – F)
Como V + F = A + 2, temos que (A – F) = (V – 2)
OU Sif = 360º . (V – 2)

18.  Um poliedro é chamado
convexo, em relação a
uma de suas faces, se
está todo contido no
mesmo semi-espaço
determinado por esta
mesma face. Caso
contrário ele será não-
convexo.

19.  De acordo com o número de faces,os
poliedros convexos possuem nomes
especiais.
Nº de faces Nome do poliedro
4 Tetraedro
5 Pentaedro
6 Hexaedro
7 Heptaedro
8 Octaedro

20. Nº de faces Nome do poliedro
9 Eneaedro
10 Decaedro
11 Undecaedro
12 Dodecaedro
13 Tridecaedro
14 Tetradecaedro
15 Pentadecaedro
20 Icosaedro

21.  Se V, A e F denotam o número de vértices,
arestas e faces, respectivamente, de qualquer
poliedro convexo, então
V – A + F = 2.

22.  Um poliedro convexo é chamado regular se:
 As suas faces forem polígonos regulares, todas
com o mesmo número de lados;
 Os seus ângulos poliédricos possuem a mesma
medida.

23.  Existem apenas cinco poliedros regulares
 Tetraedro
 Hexaedro ou Cubo
 Octaedro
 Dodecaedro
 Icosaedro

24.  Diz-se que um poliedro é platônico se, e
somente se:
I. for convexo;
II. em todo vértice concorrer o mesmo número de
arestas; (m)
III. toda face tiver o mesmo número de arestas; (n)
IV. for válida a relação de Euler. (F – A + V = 2)

25.  De fato,
 Por III. temos que cada umas das F faces tem
n arestas ( n≥3 ), e como cada aresta está
presente em duas faces, temos
n
A
FAFn
2
.2. =⇒= (*)

26.  Por II. cada um dos V vértices tem m arestas
( m≥3 ), e como cada aresta tem dois vértices,
temos
m
A
VAVm
2
.2. =⇒= (**)

27.  Por IV. vale a Relação de Euler
V −A+F=2
 Substituindo (*) e (**) em (***) teremos
Anm
n
A
A
m
A
FAV
11
2
11
2
22
2
=+−⇒
⇒=+−⇒=+−
(***)
(i)

28.  Se tivéssemos m e n, simultaneamente, maiores
que 3, ocorreria uma contradição em (i), visto que A,
representando o número de arestas, deve ser
positivo. Observe:
00
1
0
1
2
11
2
111
4
11
43
4
11
43
≤⇒≤⇒
⇒≤+−⇒≤+⇒












≤⇒≥⇒>
≤⇒≥⇒>
A
A
nmnm
n
nn
m
mm

29.  Dessa forma:
 Quando m = 3, em (i) teremos:
ou seja, faces triangulares (n=3) ou faces
quadrangulares (n=4) ou faces pentagonais
(n=5)
60
1
6
111
6
111
2
1
3
111
2
11
<⇒>+−⇒=+−⇒=+−⇒=+− n
nAnAnAnm

30.  Dessa forma:
 Quando n = 3, em (i) teremos:
ou seja, vértice com três arestas(m=3) ou
quatro arestas (m=4) ou cinco arestas (m=5)
60
1
6
111
6
11
3
1
2
1111
2
11
<⇒>+−⇒=+−⇒=+−⇒=+− m
mAmAmAnm

31.  Dessa maneira
analisando as
possibilidades
teremos:
m n A V F Poliedro
3 3 3 4 4 Tetraedro
3 4 12 8 6 Hexaedro
3 5 30 20 12 Dodecaedro
4 3 12 6 8 Octaedro
5 3 30 12 20 Icosaedro

32.  Já os gregos reconheciam que só podem existir 5 sólidos
platônicos, logo só existem também 5 poliedros regulares.
Vamos tentar verificar que isso é verdade.
 Cada ângulo poliédrico (constituído por todas as faces que
convergem num vértice) terá de ter menos de 360 graus.
Por outro lado, cada um desses ângulos terá de ter pelo
menos 3 faces . Logo as faces só podem ser triângulos
(âng. interno 60º), quadrados (âng. internos 90º)
e pentágonos (âng. interno 108º).
 Repare-se que com Hexágonos regulares tal seria um
absurdo: a amplitude dos seus ângulos internos é 120º e...
3 vezes 120º dá 360º!!!

33.  Analisemos, individualmente, cada um dos casos:
 Triângulos eqüiláteros:
 Como cada ângulo interno é de 60º pode existir em
cada vértice 3, 4 ou 5 triângulos. Logo:
 3 triângulos em cada vértice obtém-se um
Tetraedro (1)
 4 triângulos em cada vértice obtém-se um Octaedro
(2)
 5 triângulos em cada vértice obtém-se um Icosaedro
(3)

34.  Quadrados:
 Como cada ângulo interno mede 90º só pode
existir em cada vértice ter 3 quadrados. Logo,
tem-se um cubo (4)
 Pentágonos:
 Como cada ângulo interno mede 108º só
podem ter 3 em cada vértice, temos o
Dodecaedro (5)

35. 4 Faces
4 Vértices
6 Arestas

36. 6 Faces
8 Vértices
12 Arestas

37. 8 Faces
6 Vértices
12 Arestas

38. 12 Faces
20 Vértices
30 Arestas

39. 20 Faces
12 Vértices
30 Arestas

40.  O Dual de um Sólido é um outro
sólido que se obtém unindo os
pontos centrais das faces
adjacentes do sólido original.

41. Dualidade Tetraedro /
Tetraedro
Dualidade Cubo / Octaedro
Dualidade Octaedro /
Cubo
Dualidade Dodecaedro / Icosaedro
Dualidade Icosaedro / Dodecaedro
O Dual de um sólido Platônico é sempre um sólido Platônico,

42. O que mostramos antes, põe em evidência uma certa
repartição dos 5 poliedros regulares em 3 classes:
Tetraedro (dual de si próprio)
 Cubo dual do Octaedro
 Dodecaedro dual do Icosaedro.
Se você comparar o número de faces e de vértices entre os
pares duais: Cubo/Octaedro e Dodecaedro/Icosaedro e
tetraedro / tetraedro, chegará a uma interessante conclusão,
qual?

43.  Em ornamentações, luminárias, prédios,
telhados, etc.
 As bolas de futebol que são poliedros
formados por pentágonos e hexágonos.
 Formas naturais de minerais e pedras
preciosas.
 Alguns vírus (verrugas e poliomielite) têm a
forma de um icosaedro.
 As colméias das abelhas são prismas
hexagonais.

44. Em obras de artes

45. Pirâmides - Egito

46. Telhado Poliédrico - Caracas

47. Parque Infantil

48. Alguns poliedros feitos de papel (Origami)

49.  A geometria permite a percepção e a visualização do espaço, o reconhecimento
de formas, a abstração de formas e a capacidade de representá-las através do
desenho ou da construção do que foi idealizado, habilidades importantes
também em outras áreas de conhecimento como a geografia, as ciências, as
artes.
 Tem muitas aplicações no mundo real, sendo uma parte mais “concreta” da
matemática, além de possibilitar outras formas de comunicação.
 A geometria é um tópico natural para encorajar a resolução de problemas.
 A geometria é excepcionalmente ricas em oportunidades para fazer explorações,
representações, construções, discussões, para que o aluno possa investigar,
descobrir, descrever e perceber propriedades.
 O trabalho com álgebra pode acostumar o indivíduo a operar sem
questionamento sobre regras pré-estabelecidas. O efetuado com a geometria
pode proporcionar o desenvolvimento de um pensamento crítico e autônomo, já
que pode favorecer a análise de fatos e relações, o estabelecimento de ligações
entre eles e a dedução.
 É um componente importante inclusive no desenvolvimento da aritmética e da
álgebra.

50.  Atividade 1 Sugestão para o professor: Embalagens
- Alunos e/ou professor trazer embalagens de tamanhos e
formatos diversificados.
- Propor que os alunos façam uma classificação em
grupo estabelecendo um critério e apresentando para o
restante da sala. (vários modos de classificar sólidos)
- Critérios que podem ser usados ou apresentados pelo
professor:
a) o que cabe dentro de cada embalagem (idéia de volume);
b) qual a forma de armazenamento considerando a variedade
das formas (usos de diferentes tipos de sólidos e suas
vantagens);
c) Quais embalagem gastam mais materiais para serem
produzidas.

51.  Atividade 2 (Aluno): Escolher algumas embalagens de
sólidos regulares para serem reproduzidas de duas maneiras:
a) Desenhando no papel, contornando os lados da embalagem;
b) Desmontando as embalagens de papel para desenhá-las no
papel.
 Atividade 3: Fazer uma investigação de quantos poliedros
podemos fazer com quadrados e triângulos, e os alunos
peguem as partes recortadas para montarem.

53. Material a ser utilizado:
✔ Um metro de barbante;
✔ Seis pedaços de canudo de mesma cor e comprimento.
Tome o fio de barbante, passe-o através de três pedaços de canudo,
construindo um triângulo e o feche por meio do um nó. Agora, passe
o restante do barbante por mais dois pedaços de canudo, juntando-
os e formando mais um triângulo com um dos lados do primeiro
triângulo. Finalmente, passe o barbante por um dos lados desse
triângulo e pelo pedaço que ainda resta, fechando a estrutura com
um nó. Essa estrutura representa as arestas de um tetraedro regular
e as etapas intermediárias de sua construção estão representadas a
seguir:

55. Material a ser utilizado:
✔ Dois metros de barbante;
✔ Doze pedaços de canudo de mesma cor e comprimento.
Com pedaços de canudos e o barbante, construa quatro triângulos e os una, dois
a dois, conforme o esquema apresentado abaixo:

56. Material a ser utilizado:
✔ Dois metros de barbante;
✔ Doze pedaços de canudo de mesma cor medindo 8
centímetros cada;
✔ Seis pedaços de canudo de mesma cor (cor diferente
dos canudos mencionados acima) medindo 11,3
centímetros.
Com os doze pedaços de canudo da mesma cor
construa um cubo de 8 cm de aresta. Para isso, passe o fio
através de quatro canudos e passe a linha novamente por
dentro do primeiro canudo, construindo um quadrado.
Considerando um dos lados desse quadrado e passando a
linha por mais três canudos, construa mais um quadrado.
Observe que ainda faltam dois canudos para completar as
arestas do cubo. Prenda-os de maneira a completá-lo. Veja
o exemplo a seguir:

57. Observe que a estrutura construída não tem rigidez
própria, pois os seus lados não ficam por si só
perpendiculares à superfície da mesa, então é
necessário tornar essa estrutura rígida. Nesse
processo, notamos que se construirmos triângulos
nas faces dessa estrutura ou no seu interior, ela se
enrijecerá.
Dando continuidade a esse raciocínio, com os seis
pedaços de canudo de cor diferente (11,3
centímetros), construa uma diagonal em cada face,
de modo que em cada vértice que determina a
diagonal cheguem mais duas diagonais.

58. Material a ser utilizado:
✔ Três metros barbante;
✔ Trinta pedaços de canudo de mesma cor e comprimento.
Construa quatro triângulos seguindo o esquema abaixo e os una obtendo
uma pirâmide regular de base pentagonal, como a desenhada na figura b
(abaixo). Repita essa construção, obtendo mais uma pirâmide. Una cada uma
das pirâmides através dos vértices das bases, por meio de pedaços de
canudos, de tal forma que em cada vértice se encontrem cinco canudos.

59. Observando as construções feitas anteriormente
(Tetraedro, Octaedro, Cubo e Icosaedro) ,
Construam o poliedro que falta para completar os
cinco sólidos regulares: O Dodecaedro.
OBS:
1. Um dodecaedro é um poliedro regular de 12 faces
2. cada face é formado por um pentágono.
3. Possui 20 vértices.
4. E possui 30 arestas ao todo.

60. ✔ Lista de materiais:
✔ 30 canudos de comprimento 7 cm para as arestas;
✔ 20 canudos de comprimento 9.8 cm, para a estrutura interna;
✔ 8 metros de barbante, que corresponde a duas passadas em cada
canudo;
✔ E muita paciência.

61. http://geometriadivertida.zip.net/
Referências para essa apresentação:
http://www.uff.br/cdme/platonicos/platonicos-html/dodecaedro.html
Referências:
MC - Construindo “esqueletos” poliédricos de Platão;
Encontro Paraibano de Educação Matemática - 2008