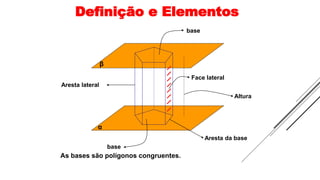
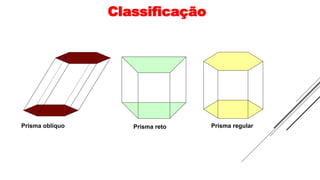
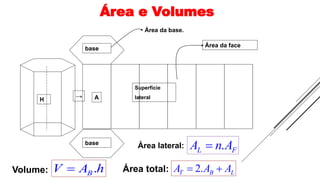
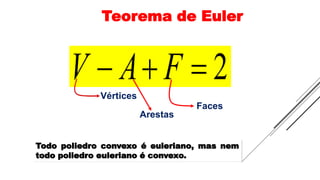
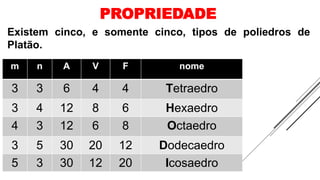
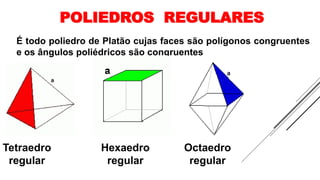
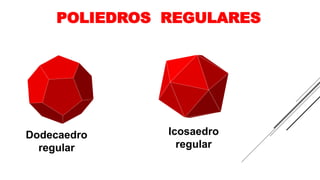
1) O documento discute vários tipos de poliedros, incluindo seus elementos, propriedades e classificações. 2) Existem cinco poliedros de Platão definidos por terem faces iguais e relações de Euler. 3) Poliedros regulares são aqueles em que as faces são polígonos congruentes e os ângulos são congruentes, incluindo o tetraedro, hexaedro e octaedro regulares.

1. POLIEDROS
Introdução à Geometria
Espacial

2. Aresta
Vértice
Ângulo
poliédrico
Face
Diagonal do poliedro
Diagonal da face
POLIEDRO CONVEXO
Elementos de um poliedro convexo

3. Teorema de Euler
Vértices
Faces
2


 F
A
V
Todo poliedro convexo é euleriano, mas nem
todo poliedro euleriano é convexo.
Arestas

4. r
V
S 4
).
2
( 

Soma dos Ângulos das Faces

5. POLIEDROS DE PLATÃO
Poliedro de Platão é todo poliedro convexo em que:
 todas as faces possuem o mesmo número de
arestas;
 todos os ângulos poliédricos possuem o mesmo
número de arestas
 é válida a relação de Euler

6. m n A V F nome
3 3 6 4 4 Tetraedro
3 4 12 8 6 Hexaedro
4 3 12 6 8 Octaedro
3 5 30 20 12 Dodecaedro
5 3 30 12 20 Icosaedro
Existem cinco, e somente cinco, tipos de poliedros de
Platão.
PROPRIEDADE

7. POLIEDROS REGULARES
É todo poliedro de Platão cujas faces são polígonos congruentes
e os ângulos poliédricos são congruentes
Tetraedro
regular
Hexaedro
regular
Octaedro
regular

8. POLIEDROS REGULARES
Dodecaedro
regular
Icosaedro
regular

9. PRISMAS

10. Definição e Elementos
α
β
base
base
Aresta da base
Aresta lateral
Face lateral
Altura
As bases são polígonos congruentes.

11. Classificação
Prisma oblíquo Prisma reto Prisma regular

12. →
H A
Superfície
lateral
base
base
Área da base.
Área da face
Área lateral:
F
L A
n
A .

Área total: L
B
T A
A
A 
 .
2
Volume: h
A
V B.

Área e Volumes

13. Paralelepípedo oblíquo Paralelepípedo retângulo
Cubo ou Hexaedro regular
Paralelepípedos

14. b
c
a
Área total: L
B
T A
A
A 
 2
Volume: H
A
V B.

Paralelepípedo Reto - Retângulo

15. a
a
a
D
Diagonal 3
a
D 
2
.
6 a
AT 
Área total
Volume
3
a
V 
Cubo