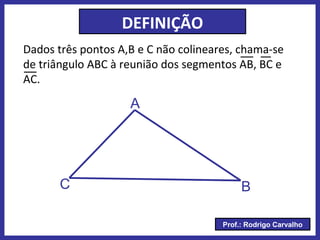
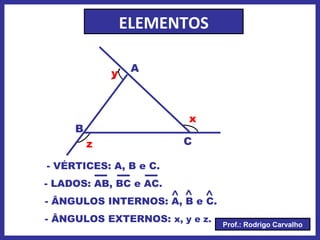
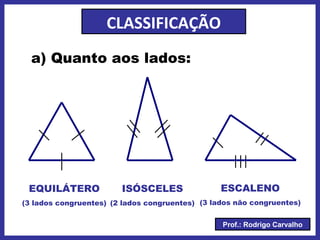
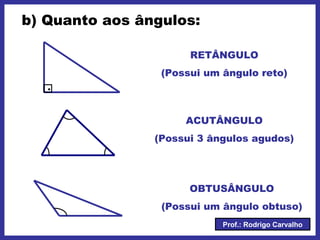
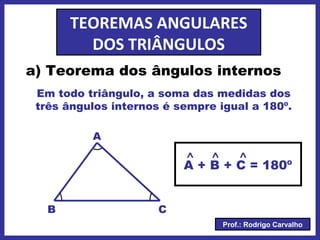
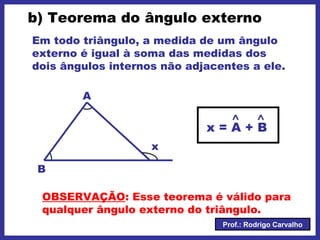
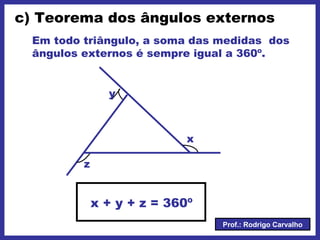
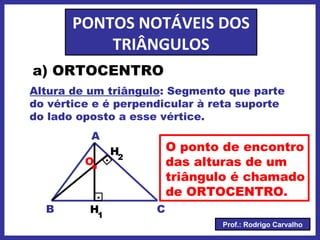
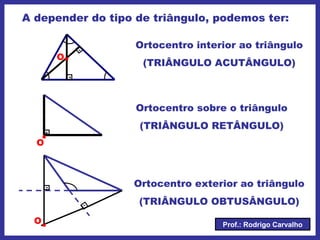
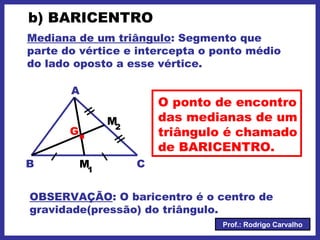
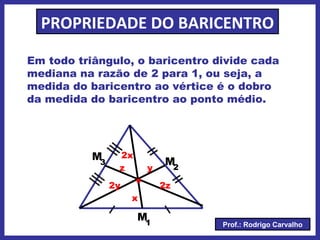
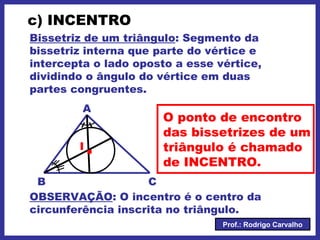
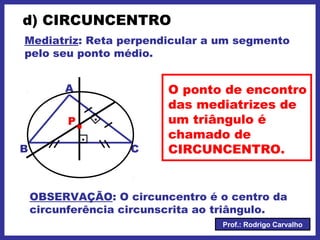
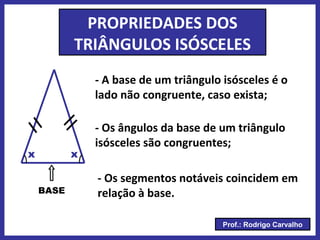
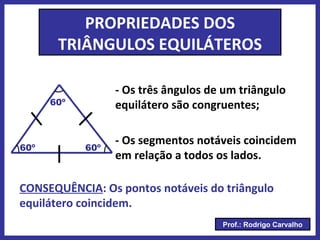
O documento define triângulo e seus elementos, classifica triângulos de acordo com lados e ângulos, apresenta teoremas e pontos notáveis de triângulos como ortocentro, baricentro e incentro. Propriedades de triângulos isósceles e equiláteros também são descritas.

1. Prof.: Rodrigo Carvalho

2. Prof.: Rodrigo Carvalho
Dados três pontos A,B e C não colineares, chama-se
de triângulo ABC à reunião dos segmentos AB, BC e
AC.
A
C B
DEFINIÇÃO

3. Prof.: Rodrigo Carvalho
ELEMENTOS
x
z
y
C
B
A
- VÉRTICES: A, B e C.
- LADOS: AB, BC e AC.
- ÂNGULOS INTERNOS: A, B e C.
- ÂNGULOS EXTERNOS: x, y e z.

4. Prof.: Rodrigo Carvalho
CLASSIFICAÇÃO
a) Quanto aos lados:
ESCALENO
(3 lados não congruentes)
EQUILÁTERO
(3 lados congruentes)
ISÓSCELES
(2 lados congruentes)

5. Prof.: Rodrigo Carvalho
b) Quanto aos ângulos:
.
RETÂNGULO
(Possui um ângulo reto)
ACUTÂNGULO
(Possui 3 ângulos agudos)
OBTUSÂNGULO
(Possui um ângulo obtuso)

6. Prof.: Rodrigo Carvalho
SÍNTESE DE CLAIRUT
É possível classificar os triângulos quanto aos ângulos,
conhecendo apenas as medidas dos seus lados. Sendo
a o maior lado do triângulo, temos :
a < b + c
a = b + c
a > b + c
2 2 2
2 2 2
2 2 2
Acutângulo
Retângulo
Obtusângulo

7. Prof.: Rodrigo Carvalho
TEOREMAS ANGULARES
DOS TRIÂNGULOS
a) Teorema dos ângulos internos
Em todo triângulo, a soma das medidas dos
três ângulos internos é sempre igual a 180º.
A
CB
A + B + C = 180º

8. Prof.: Rodrigo Carvalho
b) Teorema do ângulo externo
Em todo triângulo, a medida de um ângulo
externo é igual à soma das medidas dos
dois ângulos internos não adjacentes a ele.
A
B
x
x = A + B
OBSERVAÇÃO: Esse teorema é válido para
qualquer ângulo externo do triângulo.

9. Prof.: Rodrigo Carvalho
c) Teorema dos ângulos externos
Em todo triângulo, a soma das medidas dos
ângulos externos é sempre igual a 360º.
x
z
y
x + y + z = 360º

10. Prof.: Rodrigo Carvalho
PONTOS NOTÁVEIS DOS
TRIÂNGULOS
a) ORTOCENTRO
Altura de um triângulo: Segmento que parte
do vértice e é perpendicular à reta suporte
do lado oposto a esse vértice.
CB
A
.
.
.O
O ponto de encontro
das alturas de um
triângulo é chamado
de ORTOCENTRO.
H1
H2

11. Prof.: Rodrigo Carvalho
A depender do tipo de triângulo, podemos ter:
.
.
.O
Ortocentro interior ao triângulo
(TRIÂNGULO ACUTÂNGULO)
.
.
O
Ortocentro sobre o triângulo
(TRIÂNGULO RETÂNGULO)
.
.
.O
Ortocentro exterior ao triângulo
(TRIÂNGULO OBTUSÂNGULO)

12. Prof.: Rodrigo Carvalho
b) BARICENTRO
Mediana de um triângulo: Segmento que
parte do vértice e intercepta o ponto médio
do lado oposto a esse vértice.
CB
A
M1
M2
.G
O ponto de encontro
das medianas de um
triângulo é chamado
de BARICENTRO.
OBSERVAÇÃO: O baricentro é o centro de
gravidade(pressão) do triângulo.

13. Prof.: Rodrigo Carvalho
PROPRIEDADE DO BARICENTRO
Em todo triângulo, o baricentro divide cada
mediana na razão de 2 para 1, ou seja, a
medida do baricentro ao vértice é o dobro
da medida do baricentro ao ponto médio.
M1
M2
M3
.
x
2x
y
2y
z
2z

14. Prof.: Rodrigo Carvalho
c) INCENTRO
Bissetriz de um triângulo: Segmento da
bissetriz interna que parte do vértice e
intercepta o lado oposto a esse vértice,
dividindo o ângulo do vértice em duas
partes congruentes.
A
CB
.I
O ponto de encontro
das bissetrizes de um
triângulo é chamado
de INCENTRO.
OBSERVAÇÃO: O incentro é o centro da
circunferência inscrita no triângulo.

15. Prof.: Rodrigo Carvalho
d) CIRCUNCENTRO
Mediatriz: Reta perpendicular a um segmento
pelo seu ponto médio.
A
CB
.
.
.P
O ponto de encontro
das mediatrizes de
um triângulo é
chamado de
CIRCUNCENTRO.
OBSERVAÇÃO: O circuncentro é o centro da
circunferência circunscrita ao triângulo.

16. Prof.: Rodrigo Carvalho
PROPRIEDADES DOS
TRIÂNGULOS ISÓSCELES
- A base de um triângulo isósceles é o
lado não congruente, caso exista;
BASE
- Os ângulos da base de um triângulo
isósceles são congruentes;
xx
- Os segmentos notáveis coincidem em
relação à base.

17. Prof.: Rodrigo Carvalho
PROPRIEDADES DOS
TRIÂNGULOS EQUILÁTEROS
- Os três ângulos de um triângulo
equilátero são congruentes;
60º
60º
60º
- Os segmentos notáveis coincidem
em relação a todos os lados.
CONSEQUÊNCIA: Os pontos notáveis do triângulo
equilátero coincidem.

18. Prof.: Rodrigo Carvalho
Sugestão de exercícios:
CAPÍTULO 02
Questões: 41, 44, 46, 48, 54, 60, 61, 64, 69, 81, 86 e 94.