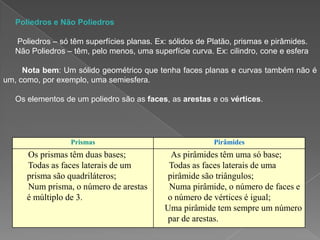
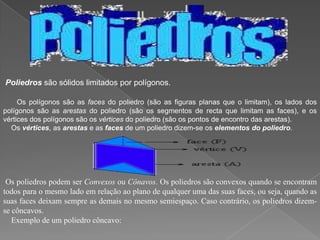
1) Platão defendia que os quatro elementos fundamentais do mundo eram representados por sólidos geométricos regulares: fogo (tetraedro), ar (octaedro), água (icosaedro) e terra (cubo). 2) Ele também acreditava na existência de um quinto sólido, o dodecaedro, que representava o universo. 3) Os sólidos de Platão eram considerados perfeitos por terem apenas faces planas.

2. SÓLIDOS DE PLATÃO
Platão era um filósofo e matemático que defendia a teoria
dos quatro “elementos” como constituintes do mundo – o
fogo (tetraedro), o ar (octaedro), a água (icosaedro) e a
terra (cubo) que são sólidos geométricos regulares. Além
disso, ainda defendia uma outra teoria. Defendia que o
mundo só poderia ter sido feito a partir de corpos perfeitos.
Mais tarde descobriu que podia existir mais um sólido
geométrico regular e deu-lhe o nome de dodecaedro que
representava o universo.

3. Poliedros e Não Poliedros
Poliedros – só têm superfícies planas. Ex: sólidos de Platão, prismas e pirâmides.
Não Poliedros – têm, pelo menos, uma superfície curva. Ex: cilindro, cone e esfera
Nota bem: Um sólido geométrico que tenha faces planas e curvas também não é
um, como, por exemplo, uma semiesfera.
Os elementos de um poliedro são as faces, as arestas e os vértices.
Prismas Pirâmides
Os prismas têm duas bases; As pirâmides têm uma só base;
Todas as faces laterais de um Todas as faces laterais de uma
prisma são quadriláteros; pirâmide são triângulos;
Num prisma, o número de arestas Numa pirâmide, o número de faces e
é múltiplo de 3. o número de vértices é igual;
Uma pirâmide tem sempre um número
par de arestas.

4. Os poliedros podem ser Convexos ou
Côncavos. Os poliedros são convexos
quando se encontram todos para o
mesmo lado em relação ao plano de
qualquer uma das suas faces, ou seja,
quando as suas faces deixam sempre
as demais no mesmo semiespaço. Caso
contrário, os poliedros dizem-se
côncavos.

5. Poliedros são sólidos limitados por polígonos.
Os polígonos são as faces do poliedro (são as figuras planas que o limitam), os lados dos
polígonos são as arestas do poliedro (são os segmentos de recta que limitam as faces), e os
vértices dos polígonos são os vértices do poliedro (são os pontos de encontro das arestas).
Os vértices, as arestas e as faces de um poliedro dizem-se os elementos do poliedro.
Os poliedros podem ser Convexos ou Cônavos. Os poliedros são convexos quando se encontram
todos para o mesmo lado em relação ao plano de qualquer uma das suas faces, ou seja, quando as
suas faces deixam sempre as demais no mesmo semiespaço. Caso contrário, os poliedros dizem-
se côncavos.
Exemplo de um poliedro côncavo:

6. Chama-se dual de um poliedro ao
poliedro que se obtém unindo por
segmentos de recta os centros das faces
consecutivas do primeiro, ou seja, ao
poliedro formado por dois poliedros, um
dentro do outro, de modo que os vértices
do sólido interior coincidam com o centro
das faces do sólido exterior.

7. Lei de Euler : F+V= A+2
Euler descobriu que num sólido poliedro a soma do nº de faces com o nº de
vértices é igual ao nº de arestas mais 2.
N.º de N.º de N.º de
Poliedro
Faces Arestas Vértices
Tetraedr
4 6 4
o
Cubo 6 12 8
Octaedr
8 12 6
o
Dodeca
12 30 20
edro
Icosaedr
20 30 12
o